河北省石家庄市晋州市2022-2023学年九年级上学期期中考试数学试题
试卷更新日期:2022-12-09 类型:期中考试
一、单选题
-
1. 一元二次方程的根为( )A、 B、 C、或 D、或2. 在中, , , , 则的值等于( )A、 B、 C、 D、3. 某同学对一组数据23,31,32,43,32,5◆,52进行统计分析时,发现其中一个两位数的个位数字被污染看不到了,则下列计算结果一定与被污数字无关的是( )A、平均数 B、中位数 C、方差 D、众数4. 某校举行体操比赛,甲、乙两个班各选18名学生参加比赛,两个班参赛学生的平均身高都是1.72米,其方差分别是 , , 则参赛学生身高比较整齐的班级是( )A、甲班 B、乙班 C、同样整齐 D、无法确定5. 下列四条线段中,能成为成比例线段的是( )A、 , , , B、 , , , C、 , , , D、 , , ,6. 下列四组图形中,一定相似的是( )A、正方形与矩形 B、正方形与菱形 C、矩形与菱形 D、正七边形与正七边形7. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 , 和 , 另一个三角形的最短边长为 , 则它的最长边为( )A、 B、 C、 D、8. 在同一平面直角坐标系中,反比例函数与一次函数(为常数,且)的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 9. 如图,一块矩形薄木板斜靠在墙角处( , 点 , , , , , , 在同一平面内),已知 , , , 则点到的距离等于( )
9. 如图,一块矩形薄木板斜靠在墙角处( , 点 , , , , , , 在同一平面内),已知 , , , 则点到的距离等于( ) A、 B、 C、 D、10. 如果关于的一元二次方程有两个不相等的实数根,那么的取值范围是( )A、 B、 C、且 D、11. 在平面直角坐标系中,有两个点 , , 若反比例函数的图象与线段有交点,则的值可能是( )A、-8 B、7 C、13 D、202312. 矩形相邻的两边长分别为25和 , 把它按如图所示的方式分割成五个全等的小矩形,每一个小矩形均与原矩形相似,则的值为( )
A、 B、 C、 D、10. 如果关于的一元二次方程有两个不相等的实数根,那么的取值范围是( )A、 B、 C、且 D、11. 在平面直角坐标系中,有两个点 , , 若反比例函数的图象与线段有交点,则的值可能是( )A、-8 B、7 C、13 D、202312. 矩形相邻的两边长分别为25和 , 把它按如图所示的方式分割成五个全等的小矩形,每一个小矩形均与原矩形相似,则的值为( )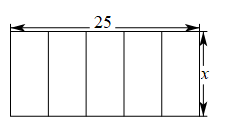 A、5 B、 C、 D、1013. 某学校举行篮球对抗赛,有支球队参加,每两队之间比赛一场,共安排了28场比赛,则正确的方程为( )A、 B、 C、 D、14. 如图所示,是由小正方形构成的网格,每个小正方形的顶点叫做格点,点 , , , , 均在格点上,则和的大小关系为( )
A、5 B、 C、 D、1013. 某学校举行篮球对抗赛,有支球队参加,每两队之间比赛一场,共安排了28场比赛,则正确的方程为( )A、 B、 C、 D、14. 如图所示,是由小正方形构成的网格,每个小正方形的顶点叫做格点,点 , , , , 均在格点上,则和的大小关系为( ) A、 B、 C、 D、无法确定15. 已知关于的一元二次方程有两个实数根,为自然数,且该方程的根也都是自然数,则符合条件的所有自然数的和为( )A、6 B、5 C、4 D、316. 如图,在平面直角坐标中,正方形与正方形是以原点为位似中心的位似图形,且位似比为 , 点 , , 在轴上,若正方形的边长为 , 则点坐标为( )
A、 B、 C、 D、无法确定15. 已知关于的一元二次方程有两个实数根,为自然数,且该方程的根也都是自然数,则符合条件的所有自然数的和为( )A、6 B、5 C、4 D、316. 如图,在平面直角坐标中,正方形与正方形是以原点为位似中心的位似图形,且位似比为 , 点 , , 在轴上,若正方形的边长为 , 则点坐标为( )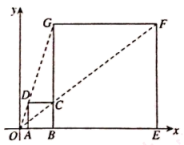 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 已知 , 点在上, , 则点到的距离为 .18. 如图,点是线段的黄金分割点, , 和均是等边三角形.若表示的面积,表示的面积,则的值为;与的大小关系为 .
 19. 定义新运算“¤”:对于任意实数 , , 都有 , 其中等式右边是通常的加法、减法和乘法运算.
19. 定义新运算“¤”:对于任意实数 , , 都有 , 其中等式右边是通常的加法、减法和乘法运算.如, .
据此,解答下列问题:
(1)、;(2)、方程的解为;(3)、若关于的方程有一个解为 , 则的值为 .三、解答题
-
20.(1)、计算:(2)、用配方法解方程:21. 如图所示,点 , 分别在的边 , 上, . 若 , 四边形的面积为 , 试求的面积.
 22. 已知:a,b,c三个数满足关系式 .(1)、填空::4: .(2)、若 , 试求出的值.(3)、在(2)的基础上,若点是反比例函数的图像上的任意一点,过点向轴引垂线,垂足为 , 请直接写出的面积.23. 甲、乙两名队员参加射击选拔赛,射击成绩见下列统计图:
22. 已知:a,b,c三个数满足关系式 .(1)、填空::4: .(2)、若 , 试求出的值.(3)、在(2)的基础上,若点是反比例函数的图像上的任意一点,过点向轴引垂线,垂足为 , 请直接写出的面积.23. 甲、乙两名队员参加射击选拔赛,射击成绩见下列统计图:
根据以上信息,整理分析数据如下:
队员
平均数(环)
中位数(环)
众数(环)
方差()
甲
7.9
4.09
乙
7
7
(1)、直接写出表格中 , , 的值;(2)、求出的值;(3)、若从甲、乙两名队员中选派其中一名队员参赛,你认为应选哪名队员?请结合表中的四个统计量,作出简要分析.24. 如图为2022年10月的日历表,在其中用一个方框圈出4个数(如图中虚框所示),设这4个数从小到大依次为 , , , . (1)、若用含有的式子分别表示出 , , , 其结果应为:;;;(2)、按这种方法所圈出的四个数中,的最大值为;(3)、嘉嘉说:“按这种方法可以圈出四个数,使得的值为135.”
(1)、若用含有的式子分别表示出 , , , 其结果应为:;;;(2)、按这种方法所圈出的四个数中,的最大值为;(3)、嘉嘉说:“按这种方法可以圈出四个数,使得的值为135.”淇淇说:“按这种方法可以圈出四个数,使最小数与最大数的乘积为84.”
请你运用一元二次方程的相关知识分别说明二人的说法是否符合题意.
25. 如图,点是的边的延长线上的一点, , , . (1)、在备用图中,确定点 , 使得点与点的距离最小(要求:尺规作图,不写作法,保留作图痕迹),并求出此时的长;(2)、如图,若 , 请求出的面积;(3)、请直接写出的值.26. 如图所示,是直角三角形, , . 点是射线上的一点,点是射线上的一点,且 , 把点绕点逆时针旋转90°落在点处,在射线上截取 , 直线和直线相交于点 .
(1)、在备用图中,确定点 , 使得点与点的距离最小(要求:尺规作图,不写作法,保留作图痕迹),并求出此时的长;(2)、如图,若 , 请求出的面积;(3)、请直接写出的值.26. 如图所示,是直角三角形, , . 点是射线上的一点,点是射线上的一点,且 , 把点绕点逆时针旋转90°落在点处,在射线上截取 , 直线和直线相交于点 . (1)、当点与点重合时,若 , 则点落在上,并与点重合,且点与点重合,如图2所示,请你直接写出此时的值及的大小.(2)、当点在如图1所示的位置时,若 , 请求出的值及的大小.(3)、当点在如图3所示的位置时,若 , 请直接写出的值及的大小,不用说明理由.
(1)、当点与点重合时,若 , 则点落在上,并与点重合,且点与点重合,如图2所示,请你直接写出此时的值及的大小.(2)、当点在如图1所示的位置时,若 , 请求出的值及的大小.(3)、当点在如图3所示的位置时,若 , 请直接写出的值及的大小,不用说明理由.