河北省保定市易县2022-2023学年九年级上学期期中考试数学试题

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列防控疫情的图标中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程 $2 x^{2} - 3 x = 1$ 的二次项系数、一次项系数、常数项分别为（）

A、2、3、1 B、2、-3、1 C、2、3、-1 D、2、-3、-1

查看试题解析
3. 若 $x = 2$ 是关于x的一元二次方程 $x^{2} - m x + 6 = 0$ 的一个根，则m的值为（）

A、 $5$ B、 $4$ C、 $3$ D、 $2$

查看试题解析
4. 对于二次函数 $y = - {(x - 4)}^{2} - 1$ ，下列说法正确的是（）

A、图象的开口向上 B、图象的对称轴是直线 $x = 4$ C、图象的顶点是 $(- 4 ， - 1)$ D、当 $x > 4$ 时， $y$ 随 $x$ 的增大而增大

查看试题解析
5. 不解方程，判断方程 $3 x^{2} - 4 x - 1 = 0$ 的根的情况是（）

A、没有实数根 B、有两个相等实数根 C、有两个不相等实数根 D、无法确定

查看试题解析
6. 如图，将△AOB绕点O按逆时针方向旋转45°后得到△A＇OB＇，若∠AOB=15°，则∠AOB＇的度数是（）

A、25° B、30° C、35° D、40°

查看试题解析
7. 若抛物线 $y = {(x + 4)}^{2} - 1$ 平移得到 $y = x^{2}$ ，则必须（）

A、先向左平移4个单位，再向下平移1个单位 B、先向右平移4个单位，再向上平移1个单位 C、先向左平移1个单位，再向下平移4个单位 D、先向右平移1个单位，再向上平移4个单位

查看试题解析
8. 用配方法解方程 $x^{2} + 4 x - 5 = 0$ 时，原方程应变形为（　　）

A、 ${(x - 2)}^{2} = 1$ B、 ${(x - 4)}^{2} = 11$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x + 4)}^{2} = 21$

查看试题解析
9. 向空中发射一枚炮弹，第x秒时的高度为y米，且高度与时间的关系为y＝ax²+bx+c（a≠0）．若此炮弹在第6秒与第18秒时的高度相等，则在下列时间中炮弹所在高度最高的是（）

A、第8秒 B、第10秒 C、第12秒 D、第15秒

查看试题解析
10. 若关于x的一元二次方程 $(k - 1) x^{2} + x + 1 = 0$ 有两个实数根，则k的取值范围是（）

A、 $k \leq \frac{5}{4}$ B、 $k < \frac{5}{4}$ C、 $k < \frac{5}{4}$ 且 $k \neq 1$ D、 $k \leq \frac{5}{4}$ 且 $k \neq 1$

查看试题解析
11. 杨倩在东京奥运会女子10米气步枪决赛中夺得冠军，为中国代表团揽入首枚金牌，随后杨倩同款“小黄鸭”发卡在电商平台上爆单．该款发卡在某电商平台上7月24日的销量为5000个，7月25日和7月26日的总销量是30000个．若7月25日和26日较前一天的增长率均为x，则可列方程为（）

A、 $5000 {(1 + x)}^{2} = 30000$ B、 $5000 + 5000 (1 + x) + 5000 {(1 + x)}^{2} = 30000$ C、 $5000 {(1 - x)}^{2} = 30000$ D、 $5000 (1 + x) + 5000 {(1 + x)}^{2} = 30000$

查看试题解析
12. 如图，将△ABC绕点C顺时针旋转得到△EDC，若点A恰好在ED的延长线上，∠BAC＝40°，则∠BAE的度数为（）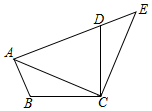

A、80° B、60° C、65° D、70°

查看试题解析
13. 如图，在6×4的方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是（）

A、点M B、格点N C、格点P D、格点Q

查看试题解析
14. 在同一平面直角坐标系中，函数y=ax+b与y=ax²-bx的图象可能是（）

A、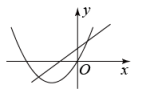 B、 C、 D、

查看试题解析
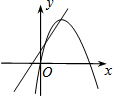15. 二次函数y=ax²+bx+c（a≠0）的图像如图所示，给出下列结论： ① $b^{2} - 4 a c ＞ 0$ ；② $2 a + b < 0$ ；③ $4 a - 2 b + c = 0$ ；④ $a + b + c ＞ 0$ ．其中正确的是（）

A、①② B、①④ C、③④ D、②③

查看试题解析
16. 如图，在Rt△ABC中，∠C＝90°，∠A＝60°，AB＝8，点P是AB边上直面的一个动点，过点P作PD⊥AB交直角边于点D，设AP为x，△APD的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

17. 已知，点A（a﹣1，3）与点B（2，﹣2b﹣1）关于原点对称，则2a+b＝.

查看试题解析
18. 将抛物线 $y = x^{2} - 4 x + 5$ 向左平移1个单位长度，再向下平移2个单位长度后经过点 $P (a ， 1)$ ，则 $2021 - a^{2} + 2 a =$ ．

查看试题解析
19. 如图，等边△ABC内有一点O，OA＝3，OB＝4，OC＝5，以点B为旋转中心将BO逆时针旋转60°得到线段 $B O^{'}$ ，连接 $A O^{'}$ ，下列结论：① $△ A B O^{'}$ 可以看成是△BOC绕点B逆时针旋转60°得到的；②点O与 $O^{'}$ 的距离为5；③∠AOB＝150°；④S_{四边形AOBO′}＝6+4 $\sqrt{2}$ ；⑤ $S_{△ A O C} + S_{△ A O B}$ ＝6+ $\frac{9}{4} \sqrt{3}$ ．其中正确的结论有．（填正确序号）

查看试题解析

三、解答题

20. 解方程：

(1)、 $x (3 + x) = 2 (3 + x)$ ；

(2)、x²+2x-14=0．

查看试题解析
21. 已知：抛物线y=-x²+bx+c经过A（-1，0）、B（5，0）两点，顶点为P．求：

(1)、求b，c的值；

(2)、求△ABP的面积．

查看试题解析
22. 如图，在足够大的空地上有一段长为20米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．

(1)、所围成的矩形菜园的面积为450平方米，求所用旧墙AD的长；

(2)、求矩形菜园ABCD面积的最大值．

查看试题解析
23. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点均在格点上，在建立平面直角坐标系后，点C的坐标为（-2，-2）．
⑴画出△ABC以y轴为对称轴的对称图形△A₁B₁C₁；
⑵以原点O为对称中心，画出△A₁B₁C₁关原点O对称的△A₂B₂C₂并写出点C₂的坐标；
⑶以 $C_{2}$ 为旋转中心，把△A₂B₂C₂顺时针旋转90°，得到△C₂A₃B₃ ．

查看试题解析
24. 体育测试时，九年级一名学生，双手扔实心球．已知实心球所经过的路线是某个二次函数图象的一部分，如果球出手处 $A$ 点距离地面的高度为 $2 m$ ，当球运行的水平距离为 $4 m$ 时，达到最大高度 $4 m$ 的 $B$ 处（如图），问该学生把实心球扔出多远？（结果保留根号）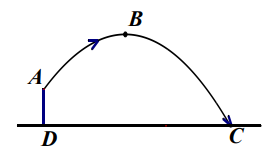

查看试题解析
25. 2022年冬奥会即将在北京召开，某网络经销商购进了一批以冬奥会为主题的文化衫进行销售，文化衫的进价为每件30元，当销售单价定为70元时，每天可售出20件，每销售一件需缴纳网络平台管理费2元，为了扩大销售，增加盈利，决定采取适当的降价措施，经调查发现：销售单价每降低1元，则每天可多售出2件（销售单价不低于进价），若设这款文化衫的销售单价为x（元），每天的销售量为y（件）．

(1)、求每天的销售量y（件）与销售单价x（元）之间的函数关系式；

(2)、当销售单价为多少元时，销售这款文化衫每天所获得的利润最大，最大利润为多少元？

查看试题解析
26. 如图，直线 $y = - \frac{1}{2} x + 2$ 与x轴交于点B，与y轴交于点C，对称轴为 $x = \frac{3}{2}$ 的抛物线经过B，C两点，与x轴负半轴交于点A．

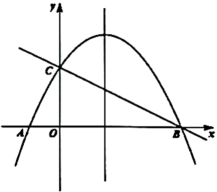(1)、求抛物线的解析式；

(2)、P为抛物线上的一点，连接 $A P$ ，将线段 $A P$ 绕点A顺时针旋转 $90 °$ 得线段 $A Q$ ，当点Q到对称轴距离为 $\frac{1}{2}$ 时，求点P的坐标；

(3)、M为抛物线上的动点，N在直线 $B C$ 上，当以O，C，M，N为顶点的四边形为平行四边形时，直接写出点N的坐标．

查看试题解析