广东省汕尾市2022-2023学年九年级上学期数学期中数学试卷

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列数学符号中，不是中心对称图形的是（）

A、∽ B、 $∥$ C、＞ D、= $=$

查看试题解析
2. 在平面直角坐标系xOy中，点A（2，3）关于原点对称的点的坐标是（）

A、（2，－3） B、（－2，3） C、（3，2） D、（－2，－3）

查看试题解析
3. 二次函数 $y = x^{2} - 6 x - 1$ 的二次项系数、一次项系数和常数项分别是（）

A、1，-6，-1 B、1，6，1 C、0，-6，1 D、0，6，-1

查看试题解析
4. 若二次函数y=mx²（m≠0）的图象经过点（2，-5），则它也经过（）

A、（-2，-5） B、（-2，5） C、（2，5） D、（-5，2）

查看试题解析
5. 已知二次函数y＝3（x-1）²+5，下列结论正确的是（）

A、其图象的开口向下 B、图象的对称轴为直线x＝-1 C、函数的最大值为5 D、当x＞1时，y随x的增大而增大

查看试题解析
6. 直线 $y = - x + 2$ 与抛物线 $y = x^{2}$ 有（）个交点．

A、0 B、1 C、2 D、3

查看试题解析
7. 如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，则∠B的大小为（）

A、30° B、40° C、50° D、60°

查看试题解析
8. 如图，将线段 $A B$ 绕一个点顺时针旋转 $9 0^{∘}$ 得到线段 $C D$ ，则这个点是（）

A、 $M$ 点 B、 $Q$ 点 C、 $P$ 点 D、 $N$ 点

查看试题解析
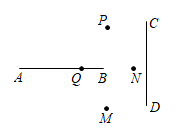9. 已知点A（﹣1，﹣1），点B（1，1），若抛物线y＝x²﹣ax+a+1与线段AB有两个不同的交点（包含线段AB端点），则实数a的取值范围是（）

A、 $- \frac{3}{2}$ ≤a＜﹣1 B、 $- \frac{3}{2}$ ≤a≤﹣1 C、 $- \frac{3}{2}$ ＜a＜﹣1 D、 $- \frac{3}{2}$ ＜a≤﹣1

查看试题解析
10. 在平面直角坐标系中，等边 $Δ A O B$ 如图放置，点 $A$ 的坐标为 $(1 ， 0)$ ，每一次将 $Δ A O B$ 绕着点 $О$ 逆时针方向旋转 $60 °$ ，同时每边扩大为原来的2倍，第一次旋转后得到 $Δ A_{1} O B_{1}$ ，第二次旋转后得到 $Δ A_{2} O B_{2}$ ， …，依次类推，则点 $A_{2021}$ 的坐标为（）

A、 $(- 2^{2020} ， - \sqrt{3} \times 2^{2020})$ B、 $(2^{2021} ， - \sqrt{3} \times 2^{2021})$ C、 $(2^{2020} ， - \sqrt{3} \times 2^{2020})$ D、 $(- 2^{2011} ， - \sqrt{3} \times 2^{2021})$

查看试题解析

二、填空题

11. 方程 $x (x - 2) = 0$ 的解为．

查看试题解析
12. 将抛物线 $y = x^{2}$ 向下平移2个单位，所得抛物线的表达式是．

查看试题解析
13. 在平面直角坐标系中，将点A（3，2）绕原点O按顺时针方向旋转90°后，其对应点A’的坐标是.

查看试题解析
14. 汽车刹车后行驶的距离s（单位：m）关于行驶时间t（单位：s）的函数解析式是 $s = - 6 t^{2} + 15 t$ ．汽车刹车后到停下来前进了m．

查看试题解析
15. 已知二次函数的y＝ax²+bx+c （a≠0）图象如图所示，有下列4个结论：①abc＜0；②b＜a+c；③2a+b＝0；④a+b＜m （am+b）（m≠1的实数），其中正确的结论有．

查看试题解析

三、解答题

16. 解方程 $3 (2 x - 3)^{2} - 2 (2 x - 3) = 0$

查看试题解析
17. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x + k + 2 = 0$ .

(1)、若 $k = - 6$ ，求此方程的解；

(2)、若该方程无实数根，求 $k$ 的取值范围.

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ，将 $R t △ A B C$ 绕点A旋转一定的角度得到 $R t △ A D E$ ，且点E恰好落在边BC上．

(1)、求证：AE平分 $∠ C E D$ ；

(2)、连接BD，求证： $∠ D B C = 90 °$ ．

查看试题解析
19. 如图，在Rt△ABC中，∠ACB=90°，∠BAC=30°，将线段CA绕点C逆时针旋转60°，得到线段CD，连接AD，BD．

(1)、依题意补全图形；

(2)、若BC=1，求线段BD的长．

查看试题解析
20. 在 $△ A B C$ 中， $∠ A C B = 9 0^{°}$ ， $A C = B C$ ，直线 $M N$ 经过点 $C$ ，且 $A D ⊥ M N$ 于点 $D$ ， $B E ⊥ M N$ 于点 $E$ ．

(1)、当直线 $M N$ 绕点 $C$ 旋转到图（1）的位置时，求证： $D E = A D + B E$ ；

(2)、当直线 $M N$ 绕点 $C$ 旋转到图（2）的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，请说明理由．

查看试题解析
21. 渠县是全国优质黄花主产地，某加工厂加工黄花的成本为30元/千克，根据市场调查发现，批发价定为48元/千克时，每天可销售500千克.为增大市场占有率，在保证盈利的情况下，工厂采取降价措施.批发价每千克降低1元，每天销量可增加50千克.

(1)、写出工厂每天的利润 $W$ 元与降价 $x$ 元之间的函数关系.当降价2元时，工厂每天的利润为多少元？

(2)、当降价多少元时，工厂每天的利润最大，最大为多少元？

(3)、若工厂每天的利润要达到9750元，并让利于民，则定价应为多少元？

查看试题解析
22. 如图，已知抛物线 $y = - x^{2} + b x + c$ 经过A(－1，0)，B(3，0)两点．

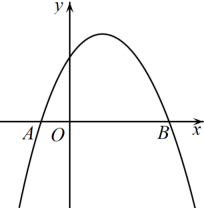(1)、求抛物线的解析式；

(2)、当0<x<3时，直接写出y的取值范围；

(3)、点P为抛物线上一点，若 $S_{△ P A B} = 10$ ，求出此时点P的坐标．

查看试题解析
23. 已知 $△ A B C$ 是等边三角形．

(1)、将 $△ A B C$ 绕点A逆时针旋转角 $θ (0 ° < θ < 180 °)$ ，得到 $△ A D E$ ， BD和EC所在直线相交于点O．
①如图a，当 $θ = 20 °$ 时， $△ A B D$ 与 $△ A C E$ 是否全等？ ▲ （填“是”或“否”）， $∠ B O E =$ ▲ 度；
②当 $△ A B C$ 旋转到如图b所在位置时，求 $∠ B O E$ 的度数；

(2)、如图c，在AB和AC上分别截取点 $B^{'}$ 和 $C^{'}$ ，使 $A B^{'} = A C^{'}$ ，连接 $B^{^{'}} C^{^{'}}$ ，将 $△ A B^{'} C^{'}$ 绕点A逆时针旋转角 $(0 ° < θ < 180 °)$ ，得到 $△ A D E$ ， BD和EC所在直线相交于点O，请利用图c探索 $∠ B O E$ 的度数，直接写出结果，不必说明理由．

查看试题解析

广东省 汕尾市2022-2023学年九年级上学期数学期中数学试卷

一、单选题

二、填空题

三、解答题

广东省汕尾市2022-2023学年九年级上学期数学期中数学试卷