广东省茂名市电白区2022-2023学年九年级上学期期中考试数学试卷

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 矩形具有而菱形不一定具有的性质是（）

A、对边分别相等 B、对角分别相等 C、对角线互相平分 D、对角线相等

查看试题解析
2. 下列各组线段中，不成比例的是（）

A、 $3 c m ， 5 c m ， 15 c m ， 9 c m$ B、 $4 c m ， 2 c m ， 3 c m ， 1 c m$ C、 $12 c m ， 3 c m ， 4 c m ， 1 c m$ D、 $10 c m ， 5 c m ， 20 c m ， 10 c m$

查看试题解析
3. 小颖、小亮和小丽三位同学随机地站成一排做游戏，小颖恰好站在中间的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
4. 如图，面积为50m²的矩形试验田一面靠墙（墙的长度不限），另外三面用20m长的篱笆围成，平行于墙的边开有一扇1m宽的门（门的材料另计）．设试验田垂直于墙的一边AB为xm，可列方程为（）

A、（20＋1-x）x＝50 B、（20-1-x）x＝50 C、（20＋1-2x）x＝50 D、（20-1-2x）x＝50

查看试题解析
5. 如图，在△ABC中，D，E，F分别是AB，AC，BC上的点，且DE $∥$ BC，EF $∥$ AB，若BF：FC＝2：3，AB＝15，则BD＝（）

A、6 B、9 C、10 D、12

查看试题解析
6. 已知 $m$ 、 $n$ 是一元二次方程 $x^{2} + x - 2022 = 0$ 的两个实数根，则代数式 $m^{2} + 2 m + n$ 的值等于（）

A、 $2019$ B、 $2020$ C、 $2021$ D、 $2022$

查看试题解析
7. 如图，一块矩形ABCD绸布的长AB=a，宽AD=1，按照图中的方式将它裁成相同的三面矩形彩旗，如果裁出的每面彩旗与矩形ABCD绸布相似，则a的值等于（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

查看试题解析
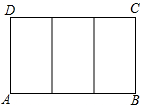8. 数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具，此时测得 $∠ D = 60 °$ ，对角线 $B D$ 长为 $8 \sqrt{3} c m$ ，改变教具的形状成为图2所示的正方形，则正方形的对角线长为（）

A、 $8 c m$ B、 $8 \sqrt{2} c m$ C、 $8 \sqrt{3} c m$ D、 $16 c m$

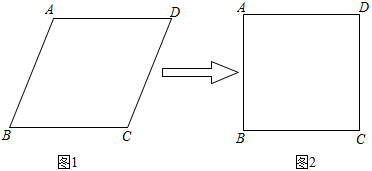查看试题解析
9. 如图，在矩形ABCD中，AB＝24，BC＝12，点E在边AB上，点F在边CD上，点G、H在对角线AC上，若四边形EGFH是菱形．则AE的长是（）

A、15 B、20 C、 $6 \sqrt{3}$ D、 $8 \sqrt{3}$

查看试题解析
10. 如图，已知正方形 $A B C D$ 和正方形 $C E G F$ ，点 $E$ 、 $H$ 分别为 $C D$ 、 $B C$ 的中点，连接 $A H 、 H G 、 C G 、 D H 、 H E 、 A G$ 和 $D G$ ，则下列结论中：① $A H ⊥ H C$ ；② $△ D H G$ 为等腰三角形；③ $△ A D G ∽ △ G C H$ ；④ $H E ∥ C G$ ，正确的有多少个？（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 在一个不透明的箱子里装有红色、蓝色、黄色的球共50个，除颜色外，形状、大小、质地等完全相同，小明通过多次摸球试验后发现摸到红色、黄色球的频率分别稳定在20%和30%，则箱子里蓝色球的个数很可能是．

查看试题解析
12. 已知关于x的方程 $(a + 1) x^{2} - 2 x + 3 = 0$ 有实数根，则整数a的最大值是．

查看试题解析
13. 中国结，象征着中华民族的历史文化与精致．小明家有一中国结挂饰，他想求两对边的距离，利用所学知识抽象出如图所示的菱形ABCD，测得 $B D = 12 c m$ ， $A C = 16 c m$ ，直线 $E F ⊥ A B$ 交两对边与E、F，则EF的长为cm．

查看试题解析
14. 已知： $\frac{y + z}{x} = \frac{x + z}{y} = \frac{x + y}{z} = k$ ，则k＝．

查看试题解析
15. 如图，在 $R t Δ A B C$ 中， $∠ C = 9 0^{∘}$ ，棱长为1的立方体的表面展开图有两条边分别在 $A C$ ， $B C$ 上，有两个顶点在斜边 $A B$ 上，则 $Δ A B C$ 的面积为．

查看试题解析

三、解答题

16. 解方程： $2 x^{2} - 4 x - 1 = 0$

查看试题解析
17. 已知： $a ： b ： c = 2 ： 3 ： 5$ .

(1)、求代数式 $\frac{3 a - b + c}{2 a + 3 b - c}$ 的值；

(2)、如果 $3 a - b + c = 24$ ，求 $a ， b ， c$ 的值.

查看试题解析
18. 如图，在△ABC中，D、E分别是边AC、BC的中点，F是BC延长线上一点，∠F＝∠B．

(1)、若AB＝10，求FD的长；

(2)、若AC＝BC，求证：△CDE∽△DFE．

查看试题解析
19. 某中学积极落实国家“双减”教育政策，决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量，促进学生全面健康发展为优化师资配备，学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程(要求必须选修一门且只能选修一门)？”的随机问卷调查，并根据结果绘制以下不完整的统计图，
请结合上述信息，解答下列问题：

(1)、共有名学生参与了本次问卷调查：“陶艺”在扇形统计图中所对应的圆心角是度；

(2)、选修“园艺”有多少人？并补全调查结果条形统计图；

(3)、小刚和小强分别从“礼仪”等五门校本课程中任选一门，请用列表法或画树状图法求出两人恰好选到同一门课程的概率．

查看试题解析
20. 已知关于x的一元二次方程x²-（2k+1）x+4k-3＝0．

(1)、求证：无论k取什么实数值，该方程总有两个不相等的实数根；

(2)、当一矩形ABCD的对角线长为AC＝ $\sqrt{31}$ ，且矩形两条边AB和BC恰好是这个方程的两个根时，求矩形ABCD的周长．

查看试题解析
21. 如图，已知在△OAB中AO＝BO，分别延长AO，BO到点C、D，使得OC＝AO，OD＝BO，连接AD，DC，CB．

(1)、求证：四边形ABCD是矩形；

(2)、以AO，BO为一组邻边作平行四边形AOBE，连接CE．若CE⊥AE，求∠AOB的度数．

查看试题解析
22. 某商业街有店面房共195间，2016年平均每间店面房的年租金为10万元，由于物价上涨，到2018年平均每间店面房的年租金上涨到了12.1万元，据预测，当每间的年租金定为12.1万元时，可全部租出；若每间的年租金每增加1万元，就要少租出10间．该商业街管委会要为租出的商铺每间每年交各种费用1.1万元，未租出的商铺每间每年交各种费用5000元．

(1)、求2016年至2018年平均每间店面房年租金的平均增长率；

(2)、当每间店面房的年租金上涨多少万元时，该商业街的年收益（收益 $=$ 租金 $-$ 各种费用）为2305万元？

查看试题解析
23. 如图，已知四边形ABCD是矩形，点E在BA的延长线上，AE＝AD，EC与BD相交于点G，与AD相交于点F，AF＝AB．

(1)、求证：BD⊥EC；

(2)、求AD：AB的值；

(3)、连接AG，求证：EG-DG＝ $\sqrt{2}$ AG．

查看试题解析