北京市大兴区2022 ~2023学年九年级上学期期中数学试卷

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 对称给人们一种美感，下列图形属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 抛物线 $y = 2 (x - 3)^{2} + 1$ 的顶点坐标是（）

A、 $(3 ， 1)$ B、 $(- 3 ， 1)$ C、 $(2 ， 1)$ D、 $(2 ， 3)$

查看试题解析
3. 将抛物线 $y = x^{2}$ 向下平移3个单位长度，得到的抛物线的函数解析式为（）

A、 $y = x^{2} - 3$ B、 $y = x^{2} + 3$ C、 $y = {(x - 3)}^{2}$ D、 $y = {(x + 3)}^{2}$

查看试题解析
4. 用配方法解方程 $x^{2} + 2 x = 1$ ，变形后的结果正确的是（）

A、 ${(x - 1)}^{2} = 2$ B、 ${(x - 1)}^{2} = 0$ C、 ${(x + 1)}^{2} = 0$ D、 ${(x + 1)}^{2} = 2$

查看试题解析
5. 在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中四个涂黑的小正方形组成的图形是中心对称图形，选择的小正方形的序号是（）

A、① B、② C、③ D、④

查看试题解析
6. 已知点 $A (- 1 ， y_{1})$ ， $B (1 ， y_{2})$ ， $C (2 ， y_{3})$ 都在二次函数 $y = (x - 1)^{2}$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系正确的是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
7. 若关于x的一元二次方程 $(a + 1) x^{2} - a^{2} - a = 0$ 有一个根是 $x = - 1$ ，则a的值为（）

A、-1 B、0 C、1 D、-1或1

查看试题解析
8. 在图形的旋转过程中，下面有四种说法：
①对应点到旋转中心的距离相等；②对应点与旋转中心所连线段的夹角等于旋转角；③旋转前、后图形的形状和大小都不变；④旋转前、后图形的位置一定会改变．
上述四种说法正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 方程 $x^{2} - 3 x = 0$ 的根为.

查看试题解析
10. 请写出一个开口向上，且其图象经过原点的抛物线的解析式．

查看试题解析
11. 已知点 $A (a ， - 2)$ 与点 $B (3 ， b)$ 关于原点O中心对称，则a+b=.

查看试题解析
12. 若方程 $x^{m} - x + 1 = 0$ 是关于x的一元二次方程，则m的值为.

查看试题解析
13. 据国家能源局数据公布显示，2022年5月份全社会用电量为6716亿千瓦时，7月份全社会用电量为8324亿千瓦时，若从5月至7月全社会用电量的月平均增长率都相同，求全社会用电量的月平均增长率．设月平均增长率为x，则所列的方程应为．

查看试题解析
14. 抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴及部分图象如图所示，则关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的两根为.

查看试题解析
15. 如图，抛物线 $y_{1} = a x^{2} (a \neq 0)$ 与直线 $y_{2} = b x + c (b \neq 0)$ 的两个交点坐标分别为 $A (- 2 ， 4)$ ， $B (1 ， 1)$ ，则当 $y_{1} < y_{2}$ 时，x的取值范围是.

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $A C = B C = 2$ ， $∠ C = 9 0^{∘}$ ，点O是AB的中点，将一块边长足够大的三角板的直角顶点放在点O处，将三角板绕点O旋转，始终保持三角板直角顶点与点O重合，一条直角边与AC相交，交点为点D，另一条直角边与BC相交，交点为点 $E$ ，则线段CD与CE的长度之和为.

查看试题解析

三、解答题

17. 解方程： $2 x^{2} - 6 = 0 .$

查看试题解析
18. 解方程： $x^{2} + 6 x + 8 = 0$

查看试题解析
19. 如图，网格中每个小正方形的边长都是单位 $1 .$

(1)、画出将 $△ A B C$ 绕点O顺时针方向旋转 $90 °$ 后得到的 $△ A^{'} B^{'} C^{'}$ ；

(2)、请直接写出 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 三点的坐标．

查看试题解析
20. 已知二次函数 $y = x^{2} - 2 x - 3 .$

(1)、二次函数 $y = x^{2} - 2 x - 3$ 的图象与x轴交于 $A ， B$ 两点 $($ 点A在点B左侧 $)$ ，求 $A ， B$ 两点的坐标；

(2)、画出此函数的图象．

查看试题解析
21. 如图，在 $Δ A B C$ 中， $∠ C A B = 7 5^{∘}$ ，在同一平面内，将 $Δ A B C$ 绕点A旋转到 $Δ A B^{'} C^{'}$ 的位置，使得 $C C^{'}$ ∥ $A B$ ，求 $∠ B A B^{'}$ 的度数．

查看试题解析
22. 已知关于x的一元二次方程 $x^{2} + (3 - k) x + 2 - k = 0 .$

(1)、求证：此方程总有两个实数根；

(2)、若此方程恰有一个根大于1，求k的取值范围．

查看试题解析
23. 小明在画一个二次函数的图象时，列出了下面几组x与y的对应值．
x
…
-2
-1
0
1
2
…
y
…
-6
-1
2
3
2
…

(1)、求该二次函数的解析式；

(2)、该二次函数的图象与直线 $y = m$ 有两个交点A，B，若A，B两点间的距离小于4，请直接写出m的取值范围．

查看试题解析
24. 双手头上前掷实心球是锻炼青少年上肢力量和全身协调性的一个项目，实心球出手后飞行的路线可以看作是抛物线的一部分，建立如图所示的平面直角坐标系，某校一名学生在投掷实心球时，从出手到落地的过程中，实心球的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系 $y = - \frac{1}{8} x^{2} + \frac{3}{4} x + 2 .$

(1)、求该同学投掷实心球时，实心球在空中飞行时竖直高度的最大值；

(2)、判断并说明，该同学此次投掷实心球的水平距离能否超过10米．

查看试题解析
25. 在正方形ABCD中， $A D = 4$ ，点E在边AB上，且 $A E = 3$ ，将线段DE绕点D逆时针方向旋转得到线段DF，连接 $E F .$

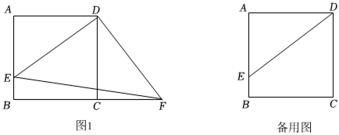(1)、如图1，若点F恰好落在边BC的延长线上，判断 $△ D E F$ 的形状，并说明理由；

(2)、若点F落在直线BC上，请直接写出 $△ D E F$ 的面积.

查看试题解析
26. 抛物线 $y = a x^{2} + b x + c (a > 0)$ 与x轴的交点坐标是 $(- 1 ， 0)$ ， $(3 ， 0) .$

(1)、请直接写出这条抛物线的对称轴；

(2)、已知点 $A (m ， y_{1})$ ， $B (m + 1 ， y_{2})$ 在抛物线上，若 $y_{1} < y_{2}$ ，求m的取值范围．

查看试题解析
27. $△ A B C$ 是等边三角形，将线段AC绕点A逆时针旋转 $α (0^{∘} < α \leq 6 0^{∘})$ 得到线段AD，连接BD，交AC于点O，连接CD，过点A作 $A P ⊥ C D$ 于点P，交BD于点E，连接 $C E .$

(1)、如图1，当 $α = 6 0^{∘}$ 时，则 $∠ B E C =$ $^{∘}$ ；

(2)、如图2，当 $0^{∘} < α < 6 0^{∘}$ 时，依题意补全图 $2 .$
①猜想（1）中结论是否仍然成立，并说明理由；
②求证： $B E = A E + C E .$

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，已知四边形 $O A B C$ 是平行四边形，点 $A (4 ， 0)$ ， $∠ A O C = 6 0^{∘}$ ，点C的纵坐标为 $\sqrt{3}$ ，点D是边BC上一点，连接 $O D$ ，将线段 $O D$ 绕点O逆时针旋转 $6 0^{∘}$ 得到线段 $O E$ ，
给出如下定义：如果抛物线 $y = a x^{2} + b x (a \neq 0)$ 同时经过点A，E，则称抛物线 $y = a x^{2} + b x (a \neq 0)$ 为关于点A，E的“伴随抛物线”．

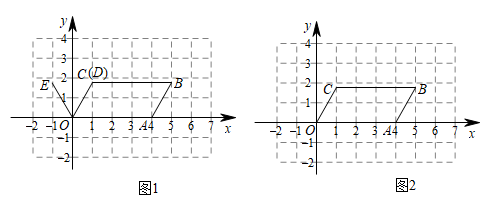(1)、如图1，当点D与点C重合时，点E的坐标为，此时关于点A，E的“伴随抛物线”的解析式为；

(2)、如图2，当点D在边 $B C$ 上运动时，连接 $C E$ ，
①当 $C E$ 取最小值时，求关于点A，E的“伴随抛物线”的解析式；
②若关于点A，E的“伴随抛物线” $y = a x^{2} + b x (a \neq 0)$ 存在，直接写出a的取值范围．

查看试题解析

x	…	-2	-1	0	1	2	…
y	…	-6	-1	2	3	2	…