安徽省芜湖市无为市2022-2023学年九年级上学期11月期中检测数学试题

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，中心对称图形是（）

A、 B、 C、 D、

查看试题解析
2. 若关于x的一元二次方程 $- 2 x^{2} - 3 x + n = 0$ 有两个不相等的实数根，则n的最小整数解是（）

A、-2 B、-1 C、0 D、1

查看试题解析
3. 下列说法中正确的是（）

A、直径是弦 B、相等的圆心角所对的弧也相等 C、圆是轴对称图形，每一条直径都是它的对称轴 D、平分弦的直径垂直于弦，并且平分弦所对的两条弧

查看试题解析
4. 抛物线 $y = {(x - a)}^{2} + a - 1$ 的顶点一定不在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 如图，将 $Δ A B C$ 绕点A逆时针旋转80°，得到 $Δ A D E$ ，若点 $D$ 在线段 $B C$ 的延长线上，则 $∠ B$ 的大小是（）

A、45° B、50° C、60° D、100°

查看试题解析
6. 如图，四边形 $A B C D$ 是⊙O的内接四边形，连接 $O A ， O C$ ．若 $∠ A B C = 108 °$ ，则 $∠ A O C$ 的度数为（）

A、72° B、108° C、144° D、150°

查看试题解析
7. 如图，“三等分角仪”由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC＝CD＝DE，点D，E可在槽中滑动，若∠BDE＝75°，则∠AOB＝（）

A、15° B、20° C、35° D、25°

查看试题解析
8. 已知：抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线 $x = 1$ ，与x轴的一个交点坐标为 $(- 1 ， 0)$ ，其部分图像如图所示，下列结论：① $a b c > 0$ ；② $b^{2} - 4 a c > 0$ ；③ $a - b + c = 0$ ；④方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个根是 $x_{1} = - 1$ ， $x_{2} = 3$ ；⑤ $8 a + c < 0$ ．其中正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 北京冬奥会跳台滑雪项目比赛其标准台高度是90m．运动员起跳后的飞行路线可以看作是抛物线的一部分，运动员起跳后的竖直高度y （单位：m）与水平距离x（单位：m）近似满足函数关系 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）．下图记录了某运动员起跳后的x与y的三组数据，根据上述函数模型和数据，可推断出该运动员起跳后飞行到最高点时，水平距离为（）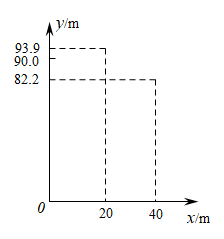

A、10m B、15m C、20m D、22.5m

查看试题解析
10. 如图，正方形 $A B C D$ 和正方形 $B E F G$ 的顶点分别在半圆O的直径和圆周上，若 $B G = 4$ ，则半圆O的半径是（）

A、 $4 + \sqrt{5}$ B、9 C、 $6 \sqrt{2}$ D、 $4 \sqrt{5}$

查看试题解析

二、填空题

11. 若x＝-1是关于x的一元二次方程ax²+bx-1＝0的一个根，则2022-2a+2b的值为．

查看试题解析
12. 如图，C，D是 $⊙ O$ 上直径 $A B$ 两侧的两点，设 $∠ A B C = 15 °$ ，则 $∠ B D C =$ ．

查看试题解析
13. 如图，正方形 $A B C D$ 的边长为2cm，正方形 $C E F G$ 的边长为1cm，若正方形 $C E F G$ 绕点C旋转，则点F到点A的距离最小值为．

查看试题解析
14. 二次函数 $y = k x^{2} - x - 4 k$ （k为常数，且k≠0）始终经过第二象限内的定点A．

(1)、定点A的坐标是；

(2)、设点A的纵坐标为 $m$ ，若该函数图象与 $y = m$ 在 $1 < x < 3$ 内没有交点，则k的取值范围是．

查看试题解析

三、解答题

15. 已知二次函数 $y = a (x - m) (x + m - 2) (a < 0)$ 与 $x$ 轴只有1个交点，且经过点 $(2 ， - 1)$ ，求二次函数的表达式．

查看试题解析
16. 在 $△ A B C$ 中， $∠ B + ∠ A C B = 30 °$ ， $A B = 4$ ， $△ A B C$ 逆时针旋转一定角度后与 $△ A D E$ 重合，且点 $C$ 恰好成为 $A D$ 中点，如图．

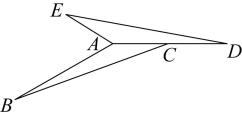(1)、旋转中心是．

(2)、求出 $∠ B A E$ 的度数和 $A E$ 的长．

查看试题解析
17. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点分别是 $A (- 3 ， 2) ， B (- 1 ， 4) ， C (0 ， 2)$ ．
⑴将 $△ A B C$ 以点O为旋转中心旋转 $180 °$ ，画出旋转后对应的 $△ A_{1} B_{1} C_{1}$ ；
⑵平移 $△ A B C$ ，若点A的对应点 $A_{2}$ 的坐标为 $(- 5 ， - 2)$ ，画出平移后对应的 $△ A_{2} B_{2} C_{2}$ ；
⑶若将 $△ A_{1} B_{1} C_{1}$ 绕某一点旋转可以得到 $△ A_{2} B_{2} C_{2}$ ，请直接写出旋转中心的坐标为 ▲ ．

查看试题解析
18. 如图，有一座圆弧形拱桥，它的跨度 $A B$ 为 $60 m$ ，拱高 $P M$ 为 $18 m$ ，当洪水泛滥到跨度只有 $30 m$ 时，就要采取紧急措施，若某次洪水中，拱顶离水面只有 $4 m$ ，即 $P N = 4 m$ 时，试通过计算说明是否需要采取紧急措施.

查看试题解析
19. 阅读材料： $a^{2} - 2 a b + 2 b^{2} - 8 b + 16 = 0$ ，求a，b的值．
解：∵ $a^{2} - 2 a b + 2 b^{2} - 8 b + 16 = 0$ ，
∴ $(a^{2} - 2 a b + b^{2}) + (b^{2} - 8 b + 16) = 0$ ，
∴ ${(a - b)}^{2} + {(b - 4)}^{2} = 0$ ，
∴ ${(a - b)}^{2} = 0 ， {(b - 4)}^{2} = 0$ ，
∴ $a = 4 ， b = 4$ ．
根据你的观察，探究下面的问题：

(1)、若 $m^{2} + n^{2} - 4 m + 4 = 0$ ，则m＝， n＝；

(2)、已知 $x^{2} + 2 y^{2} + 10 y + 25 - 2 x y = 0$ ，求 $x y$ 的值．

查看试题解析
20. 如图，直线 $y = \frac{1}{2} x + 1$ 与抛物线 $y = \frac{1}{2} x^{2} - 4 x + 8$ 交于B，C两点（B在C的左侧）．

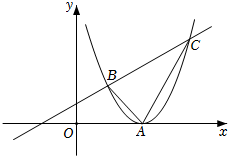(1)、求B，C两点坐标；

(2)、记抛物线的顶点为A，求△ABC的面积．

查看试题解析
21. 如图，O为半圆的圆心，C、D为半圆上的两点，连接CD、BD、AD， $C D = B D$ ．连接AC并延长，与BD的延长线相交于点E．

(1)、求证： $C D = D E$ ；

(2)、若 $A C = 6$ ，半径 $O B = 5$ ，求BD的长．

查看试题解析
22. 2022年2月20日，北京冬奥会顺利闭幕，冬奥会带来了冰雪消费热．某商场决定购进“冰墩墩”和“雪容融”两种纪念品进行销售，已知每件“冰墩墩”比每件“雪容融”的进价高30元，用1000元购进“冰墩墩”的数量和用400元购进“雪容融”的数量相同．经市场调查，整理出“冰墩墩”的售价x（元/件）与销量的关系如表：
售价x（元/件）
$50 \leq x \leq 60$
$60 < x \leq 80$
销售量（件）
100
$400 - 5 x$

(1)、求“冰墩墩”和“雪容融”每件的进价分别为多少元？

(2)、求出当x为何值时，售出“冰墩墩”所获利润最大，最大利润为多少？

查看试题解析
23. 如图，将矩形ABCD绕着点B逆时针旋转得到矩形GBEF，使点C恰好落到线段AD上的E点处，连接CE，连接CG交BE于点H．

(1)、求证：CE平分∠BED；

(2)、取BC的中点M，连接MH，求证：MH $∥$ BG；

(3)、若BC＝2AB＝4，求CG的长．

查看试题解析

售价x（元/件）	$50 \leq x \leq 60$	$60 < x \leq 80$
销售量（件）	100	$400 - 5 x$