安徽省蚌埠市蚌山区2022-2023学年九年级上学期11月期中数学试题

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $\frac{a}{b} = \frac{1}{3}$ ，则 $\frac{a}{a + b}$ 的值为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{5}$

查看试题解析
2. 点 $(- 3 ， 4)$ 在反比例函数 $y = \frac{k}{x}$ 的图象上，则下列各点在此函数图象上的是（）

A、 $(2 ， 6)$ B、 $(- 4 ， 3)$ C、 $(- 6 ， - 2)$ D、 $(3 ， 4)$

查看试题解析
3. 下列抛物线中，与抛物线 $y = x^{2} - 2 x + 4$ 具有相同对称轴的是（）

A、 $y = 4 x^{2} + 2 x + 1$ B、 $y = x^{2} - 4 x$ C、 $y = 2 x^{2} - x + 4$ D、 $y = - 2 x^{2} + 4 x$

查看试题解析
4. 下列命题中，是假命题的是（）．

A、两个等边三角形相似 B、有一个角为20°的两个直角三角形相似 C、两个等腰直角三角形相似 D、两个直角三角形相似

查看试题解析
5. 若点 $A (- 1 ， y_{1}) ， B (1 ， y_{2}) ， C (3 ， y_{3})$ 在反比例函数 $y = \frac{9}{x}$ 的图像上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
6. 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”．如图，P为AB的黄金分割点 $(A P > P B)$ ，如果AB的长度为8cm，那么AP的长度是（）cm．

A、 $4 - 2 \sqrt{5}$ B、 $4 \sqrt{5} - 4$ C、 $4 \sqrt{5} + 4$ D、 $4 - 4 \sqrt{5}$

查看试题解析
7. 已知在 $Δ A B C$ 中， $∠ A = 78 ° ， A B = 4 ， A C = 6$ ，下列阴影部分的三角形与原 $Δ A B C$ 不相似的是（）

A、 B、 C、 D、

查看试题解析
8. 如图， $A B ∥ C D ∥ E F$ ， AF交BE于点G，若AC＝CG，AG＝FG，则下列结论错误的是（）

A、 $\frac{D G}{B G} = \frac{1}{2}$ B、 $\frac{D G}{B E} = \frac{1}{3}$ C、 $\frac{C G}{C F} = \frac{1}{3}$ D、 $\frac{C D}{E F} = \frac{1}{2}$

查看试题解析
9. 如图，点A，B都在格点上（网格小正方形的边长为1），点C是线段AB与网格线的交点，则AC 的长为（）

A、 $\sqrt{13}$ B、 $\frac{4 \sqrt{13}}{3}$ C、2 $\sqrt{13}$ D、3 $\sqrt{13}$

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ 与x轴交于P，Q两点，它们的横坐标分别是p，q（其中 $p < q$ ）．对于任意的 $x \geq 0$ ，都有 $y < 0$ ，则下列说法一定正确的是（）

A、当 $x = \frac{p}{2}$ 时， $y < 0$ B、当 $x = p + q$ 时， $y = 0$ C、当 $x = \frac{q}{2}$ 时， $y < 0$ D、当 $x = \frac{p + q}{2}$ 时， $y = 0$

查看试题解析

二、填空题

11. 形状与开口方向都与抛物线 $y = - 2 x^{2}$ 相同，顶点坐标是 $(0 ， - 5)$ 的抛物线对应的函数解析式为．

查看试题解析
12. 如图，O是坐标原点，点A在函数 $y = \frac{k}{x} (x < 0)$ 的图象上， $A B ⊥ x$ 轴于B点， $△ A O B$ 的面积为4，则k的值为．

查看试题解析
13. 如图，在正方形网格中有三个三角形，分别是 $△ E B C$ ， $△ C D B$ ， $△ D E B$ ，其中与 $△ A B C$ 相似的是．

查看试题解析
14. 如图，已知矩形 $A B C D$ 对角线 $A C$ 和 $B D$ 相交于点O，点E是边 $A B$ 上一动点， $C E$ 与 $B D$ 相交于点F，连结 $O E$ ．

(1)、若点E为 $A B$ 的中点，则 $\frac{O F}{F B}$ =；

(2)、若点F为 $O B$ 的中点，则 $\frac{A E}{B E}$ = ．

查看试题解析

三、解答题

15.

(1)、已知 $\frac{a}{6} = \frac{b}{5} = \frac{c}{4}$ ，且 $a + b - 2 c = 6$ ，求a值．

(2)、已知线段 $a = 4$ cm，线段 $b = 9$ cm，线段c是线段a，b的比例中项，求线段c的长．

查看试题解析
16. 密闭容器内有一定质量的二氧化碳，当容器的体积V（单位： $m^{3}$ ）变化时，气体的密度 $ρ$ （单位： $k g / m^{}$ ）随之变化．已知密度 $ρ$ 与体积V是反比例函数关系，它的图象如图所示，当 $V = 5 m^{3}$ 时， $ρ = 1.98 k g / m^{3}$ ．

(1)、求密度 $ρ$ 关于体积V的函数解析式；

(2)、若 $3 \leq V \leq 9$ ，求二氧化碳密度 $ρ$ 的变化范围．

查看试题解析
17. 一次函数 $y = - x - 3$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象相交于 $A (- 4 ， m)$ ， $B (n ， - 4)$ 两点．

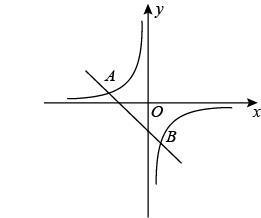(1)、求这个反比例函数的表达式；

(2)、根据图象写出使一次函数值小于反比例函数值的 $x$ 的取值范围．

查看试题解析
18. 已知：如图，在正方形ABCD中，P是BC上的点，Q是CD上的点，且AQ⊥PQ，△ADQ与△QCP是否相似？并证明你的结论．

查看试题解析
19. 已知： $△ A B C$ 中， $A D$ 为 $B C$ 上的中线，点 $E$ 在 $A D$ 上，且 $\frac{D E}{A E} = \frac{1}{3}$ ，射线 $C E$ 交 $A B$ 于点 $F$ ．求 $\frac{A F}{F B}$ 的值．

查看试题解析
20. 如图，在Rt $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 6 c m$ ， $B C = 8 c m$ ，点P从点A出发，以1cm/s的速度沿AB运动；同时，点Q从点B出发，以2cm/s的速度沿BC运动．当点Q到达点C时，P、Q两点同时停止运动．设点P、Q运动时间为 $t (s)$ ．当 $△ P B Q$ 与 $△ A B C$ 相似时， $t$ 的值是多少？

查看试题解析
21. 如图，抛物线 $y = x^{2} - b x + c$ 交x轴于点 $A (1 ， 0)$ ，交y轴交于点B，对称轴是直线 $x = 2$ ．

(1)、求抛物线的解析式

(2)、若在抛物线上存在一点D，使 $△ A C D$ 的面积为8，请求出点D的坐标．

查看试题解析
22. 在一条笔直的滑道上有黑、白两个小球同向运动，黑球在 $A$ 处开始减速，此时白球在黑球前面 $70 c m$ 处．
小聪测量黑球减速后的运动速度 $v$ （单位： $c m / s$ ）、运动距离 $y$ （单位： $c m$ ）随运动时间 $t$ （单位： $s$ ）变化的数据，整理得下表．
运动时间 $t / s$
0
1
2
3
4
运动速度 $v / c m / s$
10
9.5
9
8.5
8
运动距离 $y / c m$
0
9.75
19
27.75
36
小聪探究发现，黑球的运动速度 $v$ 与运动时间 $t$ 之间成一次函数关系，运动距离 $y$ 与运动时间 $t$ 之间成二次函数关系．

(1)、直接写出 $v$ 关于 $t$ 的函数解析式和 $y$ 关于 $t$ 的函数解析式（不要求写出自变量的取值范围）

(2)、当黑球减速后运动距离为 $64 c m$ 时，求它此时的运动速度；

(3)、若白球一直以 $2 c m / s$ 的速度匀速运动，问黑球在运动过程中会不会碰到白球？请说明理由．

查看试题解析
23. 在△ABC中，D为边AC上一点．

(1)、如图1，若 $∠ A B D = ∠ C$ ，求证： $A B^{2} = A D \cdot A C$ ；

(2)、如图2，F为线段BD上一点，且满足 $∠ A B D = ∠ A C F$
①当 $A C = 3$ ， $A B = 2$ ，点F为BD中点时，求CD的长；

②延长CF交AB于E，当点D为AC中点且 $B D = C F$ 时，直接写出 $\frac{D F}{B D}$ 的值为 ▲ ．

查看试题解析

运动时间 $t / s$	0	1	2	3	4
运动速度 $v / c m / s$	10	9.5	9	8.5	8
运动距离 $y / c m$	0	9.75	19	27.75	36