山西省大同市平城区大同六中集团校2022-2023学年八年级上学期学科竞赛学试题
试卷更新日期:2022-12-09 类型:竞赛测试
一、选择题(本大题共10小题,共30.0分。)
-
1. 下列说法中:①形状相同的两个图形是全等形;②对应角相等的两个三角形是全等三角形;③全等三角形的面积相等;④若△ABC≌△DEF,△DEF≌△MNP,则△ABC≌△MNP.其中正确的说法共有( )A、0个 B、1个 C、2个 D、3个2. 如图是一个起重机的示意图,在起重架中间增加了很多斜条,它所运用的几何原理是( )
 A、三角形两边之和大于第三边 B、三角形具有稳定性 C、三角形两边之差小于第三边 D、直角三角形的两锐角互余3. 将两个含30°和45°的直角三角板如图放置,则∠α的度数是( )
A、三角形两边之和大于第三边 B、三角形具有稳定性 C、三角形两边之差小于第三边 D、直角三角形的两锐角互余3. 将两个含30°和45°的直角三角板如图放置,则∠α的度数是( ) A、10° B、15° C、20° D、25°4. 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
A、10° B、15° C、20° D、25°4. 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( ) A、SAS B、ASA C、AAS D、SSS5. 已知三角形的三边长为3,8,x.若周长是奇数,则x的值有( )
A、SAS B、ASA C、AAS D、SSS5. 已知三角形的三边长为3,8,x.若周长是奇数,则x的值有( )
A、6个 B、5个 C、4个 D、3个6. 如图所示, , 于点 , 于点 , 交于点 , 且 , 则下列结论不一定正确的是( ) A、 B、 C、 D、7. 如图,在中,平分 , , 且分别交 , , 及的延长线于点 , , , , 若 , , 则的度数为( )
A、 B、 C、 D、7. 如图,在中,平分 , , 且分别交 , , 及的延长线于点 , , , , 若 , , 则的度数为( ) A、 B、 C、 D、8. 如图所示,中,点、、分别在三边上,是的中点,、、交于一点 , , , , 则的面积是( )
A、 B、 C、 D、8. 如图所示,中,点、、分别在三边上,是的中点,、、交于一点 , , , , 则的面积是( ) A、25 B、30 C、35 D、409. 下列条件中,不能判定两个直角三角形全等的是( )A、一个锐角和斜边对应相等 B、两条直角边对应相等 C、两个锐角对应相等 D、斜边和一条直角边对应相等10. 如图,在四边形中, , , , 则四边形的面积为( )
A、25 B、30 C、35 D、409. 下列条件中,不能判定两个直角三角形全等的是( )A、一个锐角和斜边对应相等 B、两条直角边对应相等 C、两个锐角对应相等 D、斜边和一条直角边对应相等10. 如图,在四边形中, , , , 则四边形的面积为( ) A、15 B、12.5 C、14.5 D、17
A、15 B、12.5 C、14.5 D、17二、填空题(本大题共5小题,共15.0分)
-
11. 如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是(填出一个即可).
 12. 如图,正五边形 , 平分 , 平分正五边形的外角 , 则 度
12. 如图,正五边形 , 平分 , 平分正五边形的外角 , 则 度 13. 如图,已知 , 为的中点,若 , , 则 .
13. 如图,已知 , 为的中点,若 , , 则 . 14. 根据如图所表示的已知角的度数,求出其中的度数为 .
14. 根据如图所表示的已知角的度数,求出其中的度数为 . 15. 如图,平分 , , , 垂足分别为 , 下列结论中成立的有填写正确结论的序号 .
15. 如图,平分 , , , 垂足分别为 , 下列结论中成立的有填写正确结论的序号 .;;平分 .

三、解答题(本大题共6小题,共55.0分。)
-
16. 如图,已知中,平分交于 , 于 , 若 , , 求的度数.
 17. 已知:如图,∠BAC=∠DAM,AB=AN,AD=AM,求证:∠B=∠ANM.
17. 已知:如图,∠BAC=∠DAM,AB=AN,AD=AM,求证:∠B=∠ANM.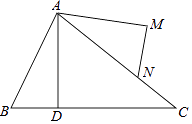 18. 如图, 于 , 于 ,若 , .求证: 平分 .
18. 如图, 于 , 于 ,若 , .求证: 平分 .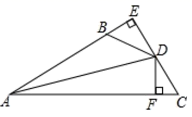 19. 如图,为的高,为上一点,交于点 , 且有 , 求证: .
19. 如图,为的高,为上一点,交于点 , 且有 , 求证: .证明: ,
.
在和中,
≌ .
.
上面的证明过程正确吗?如果错误,说明错在哪里,并写出正确的证明过程.
 20. 下面是小明解决一道课本练习题的过程及反思,请认真阅读并完成相应学习任务:
20. 下面是小明解决一道课本练习题的过程及反思,请认真阅读并完成相应学习任务:一道课后练习题的解答与思考
问题:如图,要测量池塘两岸相对两点 , 的距离,可以在池塘外取的垂线上的两点 , , 使 , 再画出的垂线 , 使与 , 在一条直线上,这时测得的长就是的长.为什么?

理由如下:
, ,
.
在和中,
,
≌依据 ,
依据2),
测得的长就是的长.
反思:由于本题中 , 且为的中点,因而可以用全等三角形的有关知识把的长度转化为的长度.所以当我们遇到“平行线和中点”的有关问题时,常常可以构造“”型全等三角形解决问题,达到转化线段或角的目的.
任务一:上述材料中的依据1,依据2分别指的是什么?
依据1: ▲ ;
依据2: ▲ .
任务二:如图,四边形中, , 点是的中点,求证: .
 21. 已知和中, , , , 与交于点 .
21. 已知和中, , , , 与交于点 . (1)、如图1当时.求证:
(1)、如图1当时.求证:≌;
;
(2)、如图2当时,直接写出的度数为;(3)、如图3,直接写出的度数为 用含的式子表示 .