辽宁省沈阳市铁西区2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、选择题（每小题2分，共20分）

1. 边长为1的正方形的对角线的长是（）

A、整数 B、分数 C、有理数 D、无理数

查看试题解析
2. 函数 $y = x - 2$ 的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 在平面直角坐标系中，点 $A (a ， 2)$ 在第二象限内，则a的取值可以是（）

A、1 B、 $- \frac{8}{3}$ C、0 D、4或－4

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $\sqrt[3]{- 5} = \sqrt[3]{5}$ C、 $\sqrt{36} = \pm 6$ D、 $- \sqrt{0.36} = - 0.6$

查看试题解析
5. 如图，已知正方形ABCD的面积为64平方厘米， $D E = 10$ 厘米，则CE的长为（）

A、6 B、12 C、 $2 \sqrt{31}$ D、 $2 \sqrt{41}$

查看试题解析
6. 按如图的运算程序，能使输出结果为3的x，y的值是（）

A、 $x = 5$ ， $y = - 2$ B、 $x = 3$ ， $y = - 3$ C、 $x = 4$ ， $y = 2$ D、 $x = - 3$ ， $y = - 9$

查看试题解析
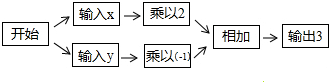7. 在平面直角坐标系 $x O y$ 中，点 $M (- 4, 2)$ 关于x轴对称的点的坐标是（）

A、 $(- 4, 2)$ B、 $(4, 2)$ C、 $(- 4, - 2)$ D、 $(4, - 2)$

查看试题解析
8. 如图， $△ A B C$ 的顶点A，B，C在边长为1的正方形网格的格点上，则AC边上的高为（）

A、 $3 \sqrt{2}$ B、 $\sqrt{2}$ C、 $\sqrt{10}$ D、 $2 \sqrt{10}$

查看试题解析
9. 已知一次函数 $y = k x - k$ 过点 $(- 1 ， 4)$ ，则下列结论正确的是（）

A、y随x增大而增大 B、 $k = 2$ C、一次函数的图象过点 $(1 ， 0)$ D、一次函数的图象与坐标轴围成的三角形面积为2

查看试题解析
10. 如图1，在 $△ A B C$ 中， $B A = B C$ ， $B D ⊥ A C$ 于点 $D (A D > B D)$ ，动点M从点A出发，沿折线 $A B \to B C$ 方向运动，运动到点C停止．设点M的运动路程为x， $△ A M D$ 的面积为y，y与x的函数图象如图2所示，则 $A D + B D$ 的值为（）

A、3 B、5 C、6 D、9

查看试题解析

二、填空题（每小题3分，共18分）

11. $\sqrt{{(- 2)}^{4}} =$ ．

查看试题解析
12. 若点 $P (2 m - 6 ， m + 2)$ 在y轴上，则点P的坐标为．

查看试题解析
13. 计算： $\sqrt{24} + 6 \sqrt{\frac{1}{6}} =$ ．

查看试题解析
14. 一只蚂蚁沿着边长为3的正方体表面从点A出发，按照如图所示经过3个面爬到点B，则它运动的最短路径长为．

查看试题解析
15. 一条直线与x轴，y轴的正半轴分别交于点A，B，点P是线段AB上任意一点（不与点A，B重合），过点P分别作两坐标轴的垂线，与两坐标轴围成的长方形的周长为8，则点A的坐标为．

查看试题解析
16. 如图，长方形ABCD中， $A B = 3$ ， $B C = 3 \sqrt{3}$ ， $∠ C B D = 30 °$ ，点M是射线BD上一点（不与点B，D重合），连接AM，过点M作 $M N ⊥ A M$ 交直线BC于点N，若 $△ B M N$ 是等腰三角形，则 $B N =$ ．

查看试题解析

三、解答题（第17小题6分，第18、19小题各8分，共22分）

17. 计算： $(\sqrt{27} + \sqrt{\frac{1}{3}}) \times \sqrt{3} - (1 + \sqrt{3}) (2 - \sqrt{3})$ ．

查看试题解析
18. 解方程组： ${\begin{cases} 4 x - y = 30 \cdot \cdot \cdot (1) \\ x - 2 y = - 10 \cdot \cdot \cdot (2) \end{cases}$ ．

查看试题解析
19. 定义运算“@”的法则为： $x @ y = \sqrt{x^{2} y + 4}$ ，求 $(2 @ 6) @ 8$ 的值．

查看试题解析

四、解答题（每题8分，共16分）

20. 如图，在平面直角坐标系中，已知点 $A (- 4 ， 1)$ ； $B (1 ， 1)$ ， $C (- 3 ， 3)$ ．

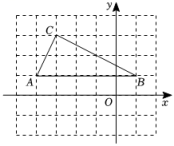(1)、判断 $△ A B C$ 的形状，并说明理由；

(2)、若点C关于直线AB的对称点为点D，则点D的坐标为；

(3)、连接CD，BD，则 $△ B C D$ 的周长为．

查看试题解析
21. 如图， $△ A B C$ 中， $A B = A C = 5$ ， $B C = 6$ ， AD平分∠BAC交BC于点D，分别以点A和点C为圆心，大于 $\frac{1}{2} A C$ 的长为半径作弧，两弧相交于点M和点N，连接MN，交AD于点E，求AE的长．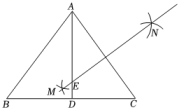

查看试题解析

五、解答题（本题10分）

22. 小刚家、学校、图书馆依次在一条直线上，小刚骑自行车匀速从学校到图书馆，到达图书馆还完书后，再以相同的速度原路返回家中，小刚离家的距离y（m）与他所用的时间x（min）的函数关系如图所示．

(1)、求小刚从图书馆返回家的过程中，y与x之间的关系式；

(2)、小刚出发35分钟时，他离家有多远？

查看试题解析

六、解答题（本题10分）

23. “互联网+”让我国经济更具活力，直播助销就是运用“互联网+”的销售方式，让大山深处的农产品远销全国各地．若要对某地特色花生与茶叶两种产品助销，已知每千克花生的售价比每千克茶叶的售价低40元，销售50千克花生与销售10千克茶叶的总售价相同．

(1)、求每千克花生、茶叶的售价；

(2)、已知花生的成本为6元/千克，茶叶的成本为36元/千克，计划两种产品共助销600千克，若花生销售m千克 $(m \geq 120)$ ，花生和茶叶的销售总利润为w元，求w的最大值．

查看试题解析

七、解答题（本题12分）

24. 如图，已知正方形ABCD的边长为5，点E为CD边上一点（不与点C，D重合），将 $△ A D E$ 沿AE所在直线折叠得到 $△ A F E$ ，延长EF交边BC于点G，连接AG，CF，可得 $∠ E A G = 45 °$ ．

(1)、判断BG与FG是否相等，并说明理由；

(2)、若 $A G ∥ C F$ ，求DE的长；

(3)、若 $F C = F G$ ，请直接写出 $\frac{S_{△ C E F}}{S_{△ C E G}}$ 的值．

查看试题解析

八、解答题（本题12分）

25. 如图，在平面直角坐标系中，直线 $y = k x + b$ 分别交x轴，y轴于点 $A (- 2 ， 0)$ ， $B (0 ， 2)$ ．点 $C (a ， 7)$ 在直线 $y = k x + b$ 上，过点C的另一条直线交x轴于点 $D (3 ， 0)$ ，点P是直线CD上一点．

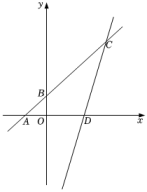(1)、求a的值；

(2)、设点P的横坐标为m， $△ A P C$ 的面积为S，请直接写出S与m之间的关系式；

(3)、若直线 $y = x + n$ 交坐标轴于点M，交直线CD于点N；点 $E (2 ， - 9)$ ，当 $∠ E M N = 90 °$ 时，请直接写出点N的坐标．

查看试题解析