广东省广州三中2022-2023学年九年级(上)期中数学试卷
试卷更新日期:2022-12-09 类型:期中考试
一、选择题(本大题共10小题,共30.0分。)
-
1. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 用配方法解一元二次方程 , 下列配方正确的是( )A、 B、 C、 D、5. 在平面直角坐标系中,将抛物线先向右平移1个单位长度,再向下平移2个单位长度,得到的新抛物线的解析式为( )A、 B、 C、 D、6. 如图,把绕点顺时针旋转 , 得到 , 交于点 , 若 , 则度数为( )
2. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 用配方法解一元二次方程 , 下列配方正确的是( )A、 B、 C、 D、5. 在平面直角坐标系中,将抛物线先向右平移1个单位长度,再向下平移2个单位长度,得到的新抛物线的解析式为( )A、 B、 C、 D、6. 如图,把绕点顺时针旋转 , 得到 , 交于点 , 若 , 则度数为( ) A、 B、 C、 D、7. 某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为 , 那么满足的方程是( )A、 B、 C、 D、8. 已知点 , , 都在二次函数的图象上,则( )A、 B、 C、 D、9. 菱形的一条对角线长为 , 边的长是方程的一个根,则菱形的周长等于( )A、 B、 C、 D、或10. 在等边三角形中,边上的点从顶点出发,向顶点运动,同时,边上的点从顶点出发,向顶点运动, , 两点运动速度的大小相等,设 , , 与的函数图象如图,图象过点 , 则图象最低点的纵坐标是( )
A、 B、 C、 D、7. 某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为 , 那么满足的方程是( )A、 B、 C、 D、8. 已知点 , , 都在二次函数的图象上,则( )A、 B、 C、 D、9. 菱形的一条对角线长为 , 边的长是方程的一个根,则菱形的周长等于( )A、 B、 C、 D、或10. 在等边三角形中,边上的点从顶点出发,向顶点运动,同时,边上的点从顶点出发,向顶点运动, , 两点运动速度的大小相等,设 , , 与的函数图象如图,图象过点 , 则图象最低点的纵坐标是( )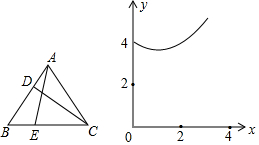 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
11. x2=x的解是.
12. 如图,以正方形的中心为原点建立平面直角坐标系,若点的坐标为 , 则点的坐标是 . 13. 已知关于的方程是一元二次方程,则的取值范围是 .14. 如果一条抛物线的形状、开口方向均与抛物线相同,且顶点坐标是 , 则它的解析式是 .15. 某种型号的小型无人机着陆后滑行的距离米关于滑行的时间秒的函数解析式是 , 无人机着陆后滑行秒才能停下来.16. 如图,是等边内一点, , , , 将线段以点为旋转中心逆时针旋转得到线段 , 下列结论:可以由绕点逆时针旋转得到;;;四边形面积 , 其中正确的结论是 .
13. 已知关于的方程是一元二次方程,则的取值范围是 .14. 如果一条抛物线的形状、开口方向均与抛物线相同,且顶点坐标是 , 则它的解析式是 .15. 某种型号的小型无人机着陆后滑行的距离米关于滑行的时间秒的函数解析式是 , 无人机着陆后滑行秒才能停下来.16. 如图,是等边内一点, , , , 将线段以点为旋转中心逆时针旋转得到线段 , 下列结论:可以由绕点逆时针旋转得到;;;四边形面积 , 其中正确的结论是 .
三、计算题(本大题共1小题,共4.0分)
-
17. 解方程:公式法
四、解答题(本大题共8小题,共68.0分。)
-
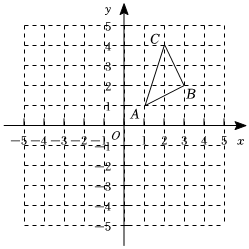
18. 如图,正方形网格中,每一个小正方形的边长都是1个单位长度,在平面直角坐标系内,的三个顶点坐标分别为 , , 画出关于原点对称的 , 直接写出点的坐标;
 19. 在平面直角坐标系中,二次函数的对称轴为 , 且它经过点 , 求该二次函数的解析式和顶点坐标.20. 如图,依靠一面长18米的墙,用38米长的篱笆围成一个矩形场地 , 设长为米.
19. 在平面直角坐标系中,二次函数的对称轴为 , 且它经过点 , 求该二次函数的解析式和顶点坐标.20. 如图,依靠一面长18米的墙,用38米长的篱笆围成一个矩形场地 , 设长为米. (1)、用含有的代数式表示的长,并直接写出的取值范围;(2)、当矩形场地的面积为180平方米时,求的长.21. 如图,在平面直角坐标系中,抛物线的图象与轴交于、两点,与直线交于点、 , 其中点坐标为 , 点坐标为 .
(1)、用含有的代数式表示的长,并直接写出的取值范围;(2)、当矩形场地的面积为180平方米时,求的长.21. 如图,在平面直角坐标系中,抛物线的图象与轴交于、两点,与直线交于点、 , 其中点坐标为 , 点坐标为 . (1)、求此抛物线的函数解析式.(2)、根据图象,直接写出时,的取值范围.22. 已知关于的方程 .(1)、若该方程的一个根为1,求的值及该方程的另一根;(2)、求证:二次函数的图象与轴有两个交点.23. 如图,将矩形绕着点按顺时针方向旋转得到矩形 , 使点落在边上的点处,连接交于点 , 连接 .
(1)、求此抛物线的函数解析式.(2)、根据图象,直接写出时,的取值范围.22. 已知关于的方程 .(1)、若该方程的一个根为1,求的值及该方程的另一根;(2)、求证:二次函数的图象与轴有两个交点.23. 如图,将矩形绕着点按顺时针方向旋转得到矩形 , 使点落在边上的点处,连接交于点 , 连接 . (1)、求证:平分;(2)、取中点 , 连接 , 求证:;24. 在正方形中,点 , 分别在边 , 上,且 .
(1)、求证:平分;(2)、取中点 , 连接 , 求证:;24. 在正方形中,点 , 分别在边 , 上,且 .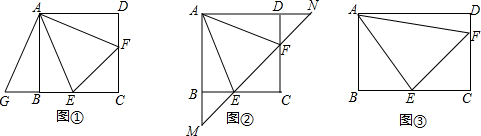 (1)、若点在边的延长线上,且 , 如图 , 求证:≌;(2)、若直线与 , 的延长线分别交于点 , 如图 , 求证:;(3)、将正方形改为长与宽不相等的矩形如图 , , , , 请你直接写出的面积.25. 如图,抛物线 与x轴相交于A(3,0)、B两点,与y轴交于点C(0,3),点B在x轴的负半轴上,且 .
(1)、若点在边的延长线上,且 , 如图 , 求证:≌;(2)、若直线与 , 的延长线分别交于点 , 如图 , 求证:;(3)、将正方形改为长与宽不相等的矩形如图 , , , , 请你直接写出的面积.25. 如图,抛物线 与x轴相交于A(3,0)、B两点,与y轴交于点C(0,3),点B在x轴的负半轴上,且 .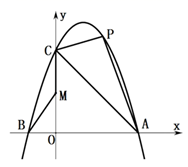
 (1)、求抛物线的函数关系式;(2)、若P是抛物线上且位于直线 上方的一动点,求 的面积的最大值及此时点P的坐标;(3)、在线段 上是否存在一点M,使 的值最小?若存在,请求出这个最小值及对应的M点的坐标;若不存在,请说明理由.
(1)、求抛物线的函数关系式;(2)、若P是抛物线上且位于直线 上方的一动点,求 的面积的最大值及此时点P的坐标;(3)、在线段 上是否存在一点M,使 的值最小?若存在,请求出这个最小值及对应的M点的坐标;若不存在,请说明理由.
-