2022-2023学年人教版数学八年级上学期期末模拟试卷
试卷更新日期:2022-12-09 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 下面图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组线段,能组成三角形的是( )A、2,3,4 B、1,2,3 C、3,4,9 D、15,12,23. 下列式子中,是因式分解的( )A、 B、 C、 D、4. 无论a取何值,下列分式总有意义的是( )A、 B、 C、 D、5. 如图,将直尺和三角板按如图的样子叠放在一起,则( )
2. 下列各组线段,能组成三角形的是( )A、2,3,4 B、1,2,3 C、3,4,9 D、15,12,23. 下列式子中,是因式分解的( )A、 B、 C、 D、4. 无论a取何值,下列分式总有意义的是( )A、 B、 C、 D、5. 如图,将直尺和三角板按如图的样子叠放在一起,则( ) A、 B、 C、 D、6. 若三角形的底边长为2a+1,该底边上的高为2a﹣1,则此三角形的面积为( )A、2a2﹣ B、4a2﹣4a+1 C、4a2+4a+1 D、4a2﹣17. 小李用7块长为8cm,宽为3cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AB=BC,∠ABC=90°),点B在DE上,点A和C分别与木墙的顶端重合,则两堵木墙之间的距离为( )
A、 B、 C、 D、6. 若三角形的底边长为2a+1,该底边上的高为2a﹣1,则此三角形的面积为( )A、2a2﹣ B、4a2﹣4a+1 C、4a2+4a+1 D、4a2﹣17. 小李用7块长为8cm,宽为3cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AB=BC,∠ABC=90°),点B在DE上,点A和C分别与木墙的顶端重合,则两堵木墙之间的距离为( ) A、36 B、32 C、28 D、218. 如图,用直尺和圆规作一个角 , 等于已知角∠AOB,能得出 , =∠AOB的依据是( )
A、36 B、32 C、28 D、218. 如图,用直尺和圆规作一个角 , 等于已知角∠AOB,能得出 , =∠AOB的依据是( ) A、SAS B、ASA C、AAS D、SSS9. 一辆汽车沿A地北偏东50方向行驶6千米到达B地,再沿B地南偏东10°方向行驶6千米到达C地,则此时A、C两地相距( )千米。A、12 B、 C、6 D、310. 如果 , , 是正数,且满足 , ,那么 的值为( )A、-1 B、1 C、2 D、
A、SAS B、ASA C、AAS D、SSS9. 一辆汽车沿A地北偏东50方向行驶6千米到达B地,再沿B地南偏东10°方向行驶6千米到达C地,则此时A、C两地相距( )千米。A、12 B、 C、6 D、310. 如果 , , 是正数,且满足 , ,那么 的值为( )A、-1 B、1 C、2 D、二、填空题(每题3分,共15分)
-
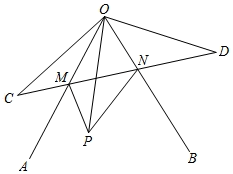
11. 已知一个包装盒的底面是内角和为720°的多边形,它是由另一个多边形纸片剪掉一个角以后得到的,则原多边形是边形.12. 已知 ,则 .13. 如图, , , AD是∠BAC内的一条射线,且 , P为AD上一动点,则的最大值是 .
 14. 照相机成像应用了一个重要原理,用公式来表示,其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示胶片(像)到镜头的距离,已知f,u,则v=.15. 如图,△ABC中,AD、BD、CD分别平分△ABC的外角∠CAE、内角∠ABC、外角∠ACF,AD∥BC.以下结论:①∠ABC=∠ACB;②∠ADC+∠ABD=90°;③BD平分∠ADC;④2∠BDC=∠BAC.其中正确的结论有 . (填序号)
14. 照相机成像应用了一个重要原理,用公式来表示,其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示胶片(像)到镜头的距离,已知f,u,则v=.15. 如图,△ABC中,AD、BD、CD分别平分△ABC的外角∠CAE、内角∠ABC、外角∠ACF,AD∥BC.以下结论:①∠ABC=∠ACB;②∠ADC+∠ABD=90°;③BD平分∠ADC;④2∠BDC=∠BAC.其中正确的结论有 . (填序号)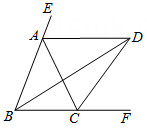
三、解答题(共8题,共75分)
-
16. 因式分解:(1)、(2)、17. 计算(1)、(2)、18. 解方程: .19. 先化简,再求值: ,其中 .20. 如图,在中, , , , 求的度数.
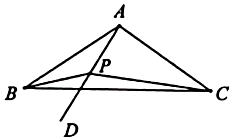
 21. 如图,和都是等腰直角三角形, , D为边上一点,请判断是否成立,并说明理由.
21. 如图,和都是等腰直角三角形, , D为边上一点,请判断是否成立,并说明理由.