人教版数学八年级上册《第十四章整式的乘法与因式分解》期末高分突破卷

试卷更新日期：2022-12-09 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 化简a³•a²的结果是（）

A、a B、a⁶ C、a⁵ D、a⁹

查看试题解析
2. 下列各式由左边到右边的变形中，是因式分解的为（　　）

A、a（x+y）＝ax+ay B、10x²﹣5x＝5x（2x﹣1） C、x²﹣4x+4＝（x﹣4）² D、x²﹣16+3x＝（x+4）（x﹣4）+3x

查看试题解析
3. 下列计算不正确的是（）

A、 $3 x y - (x^{2} - 2 x y) = 5 x y - x^{2}$ B、 $2 a^{2} b \cdot 4 a b^{3} = 8 a^{3} b^{4}$ C、 $5 x \cdot (2 x^{2} - y) = 10 x^{3} - 5 x y$ D、 $(x + 3) (x^{2} - 3 x + 9) = x^{3} + 9$

查看试题解析
4. 如图，在边长为 $a$ 的正方形中挖掉一个边长为 $b$ 的小正方形 $(a > b)$ ，把余下的部分剪拼成一个矩形，通过计算两个图形阴影部分的面积，验证了一个等式，则这个等式是（）

A、 $a^{2} - a b = a (a - b)$ B、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ C、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
5. 若 $| x + y - 5 | + (x y - 3)^{2} = 0$ ，则 $x^{2} + y^{2}$ 的值为（）

A、19 B、31 C、27 D、23

查看试题解析
6. 下列四个多项式中，能因式分解的是（　　）.

A、a²+1 B、x²+5y C、x² $-$ 5y D、a² $-$ 6a+9

查看试题解析
7. 如果 $(2 n x + 3 x^{2} + m x^{3}) (- 4 x^{2})$ 的结果中不含x的五次项，那么m的值为（）

A、1 B、0 C、-1 D、 $- \frac{1}{4}$

查看试题解析
8. 利用乘法公式计算正确的是（　　）

A、 ${(4 x - 3)}^{2} = 8 x^{2} + 12 x - 9$ B、 $(2 m + 5) (2 m - 5) = 4 m^{2} - 5$ C、 $(a + b) (a + b) = a^{2} + b^{2}$ D、 ${(4 x + 1)}^{2} = 16 x^{2} + 8 x + 1$

查看试题解析
9. 式子 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) \cdot \cdot \cdot (2^{1010} + 1)$ 化简的结果为（）

A、 $2^{1010} - 1$ B、 $2^{1010} + 1$ C、 $2^{2020} - 1$ D、 $2^{2020} + 1$

查看试题解析
10. 若干个大小形状完全相同的小长方形，现将其中4个如图1摆放，构造出一个正方形，其中阴影部分面积为40；其中5个如图2摆放，构造出一个长方形，其中阴影部分面积为100（各个小长方形之间不重叠不留空），则每个小长方形的面积为（）

A、5 B、10 C、20 D、30

查看试题解析

二、填空题（每题3分，共15分）

11. 若 $x^{3} y^{n + 1} \cdot x^{m + n} \cdot y^{2 n + 2} = x^{9} y^{9}$ ，则 $4 m - 3 n =$ ．

查看试题解析
12. 计算： $78 5^{2} - 28 5^{2} =$ ．

查看试题解析
13. 因式分解： $3 m^{2} - 6 m =$ ．

查看试题解析
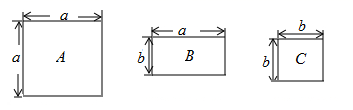
14. 若 $a + b = 8$ ， $a b = 5$ ，则 $a^{2} + b^{2} =$ ．

查看试题解析
15. 现有A、B、C三种型号的地板砖，其规格如图所示，若用这三种地板砖铺设一个长为 $3 a + 2 b$ ，宽为 $a + b$ 的长方形地面，则需要B种地砖块．

查看试题解析

三、解答题（共8题，共75分）

16. 计算：

(1)、 $3 a^{2} \cdot 2 a^{4} + {(3^{})}^{2} - 14 a^{6}$ ；

(2)、 $(2 x - 3) (2 x + 3) - {(2 x - 1)}^{2}$ ．

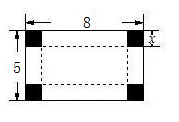
查看试题解析
17. 运用乘法公式计算：

(1)、（x－y＋z）²

(2)、（x＋2y－3z）（x－2y＋3z）

(3)、（1－x）（1＋x）（1＋x²）（1－x⁴）

(4)、 $200 0^{2} - 1996 \times 2004$

查看试题解析
18. 分解因式：

(1)、 $3 x - 12 x^{3}$

(2)、 $6 x y^{2} + 9 x^{2} y + y^{3}$

查看试题解析
19. 若x²＋px＋q与x²－3x＋2的乘积中不含x³项和x²项．求p、q的值．

查看试题解析
20. 已知实数a，b满足 $a + b = 2 ， a b = \frac{3}{4}$ ，求 $(2 a^{4} - a^{2}) \div (- a)^{2} - (a + b) (a - b)$ 的值．

查看试题解析
21. 如图，在长8cm，宽5cm的长方形塑料板的四个角剪去4个边长为 $x cm$ 的小正方形，按折痕做一个无盖的长方体盒子，求盒子的容积（塑料板的厚度忽略不计）.

查看试题解析
22. 如图，正方形 $A B C D$ 与正方形 $E F G C$ 的边长分别为 $a$ 、 $b$ ， $B$ 、 $C$ 、 $G$ 三点在同一直线上，连接 $B D$ 、 $B F$ ．

(1)、求阴影部分图形的面积 $($ 用含 $a$ 、 $b$ 的代数式表示 $)$ ．

(2)、若 $a + b = 8$ ， $a b = 15$ ，则阴影部分图形的面积为．

查看试题解析
23. 【知识回顾】
七年级学习代数式求值时，遇到这样一类题"代数式 $a x - y ＋ 6 ＋ 3 x - 5 y - 1$ 的值与x的取值无关，求a的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含x项的系数为0，即原式= $(a + 3) x - 6 y + 5$ ，所以a＋3=0，则 $a = - 3$ ．

(1)、若关于x的多项式 $(2 x - 3) m + m^{2} - 3 x$ 的值与x无关，求m的值

(2)、【能力提升】
7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分（图中阴影部分），设右上角的面积为 $S_{1}$ ，左下角的面积为 $S_{2}$ ，当AB的长变化时， $S_{1} - S_{2}$ 的值始终保持不变，求a与b的等量关系．

查看试题解析

人教版数学八年级上册《第十四章 整式的乘法与因式分解》期末高分突破卷

一、单选题（每题3分，共30分）

二、填空题（每题3分，共15分）

三、解答题（共8题，共75分）

人教版数学八年级上册《第十四章整式的乘法与因式分解》期末高分突破卷