2022-2023学年北师大版数学八年级上学期期末模拟试卷
试卷更新日期:2022-12-08 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 下列四组数能作为直角三角形三边长的是( )A、0.1,0.2,0.3 B、1,1,2 C、10,24,26 D、 , ,2. 下列计算正确的是( )A、 B、 C、 D、3. 若点和点关于轴对称,则的值为( )A、2 B、-2 C、5 D、-54. 一次函数的图像经过点 , 每当x增加1个单位时,y增加3个单位,则此函数图象向上平移2个单位长度的表达式是( )A、 B、 C、 D、5. 二元一次方程组的解是( )A、 B、 C、 D、6. 若一组数据的平均数为17,方差为2,则另一组数据的平均数和方差分别为( )A、17,2 B、17,3 C、18,1 D、18,27. 如图,点A、D、C、E在同一条直线上, , , 则的长为( )
 A、 B、 C、 D、8. 如图,直线 与 轴交于点 ,与直线 交于点 ,则关于 的不等式组 的解为( )
A、 B、 C、 D、8. 如图,直线 与 轴交于点 ,与直线 交于点 ,则关于 的不等式组 的解为( )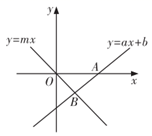 A、 B、 C、 D、9. 如图,直线与x轴,y轴分别交于点A和点B,点C在线段上,且点C坐标为 , 点D为线段的中点,点P为上一动点,当的周长最小时,点P的坐标为( )
A、 B、 C、 D、9. 如图,直线与x轴,y轴分别交于点A和点B,点C在线段上,且点C坐标为 , 点D为线段的中点,点P为上一动点,当的周长最小时,点P的坐标为( )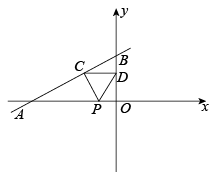 A、 B、 C、 D、10. 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
A、 B、 C、 D、10. 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:①AE+BF=AB;②△DEF始终为等腰直角三角形;③S四边形CEDF=AB2;④AE2+CE2=2DF2 .
其中正确的是( )
 A、①②③④ B、①②③ C、①④ D、②③
A、①②③④ B、①②③ C、①④ D、②③二、填空题(每题3分,共15分)
-
11. 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AC=5,BC=12,则CD=.
 12. 已知x,y为实数,且 , 则的立方根是 .13. 已知关于的方程的解为 , 则一次函数与轴交点的坐标为 .14. 为了庆祝中国共产党成立100周年,某校举行“歌唱祖国”班级合唱比赛,评委将从“舞台造型、合唱音准和进退场秩序”这三项进行打分,各项成绩均按百分制计算,然后再按舞台造型占40%,合唱音准占40%,进退场秩序占20%计算班级的综合成锁.七(1)班三项成绩依次是95分、90分、95分,则七(1)班的综合成绩为 .15. 已知二元一次方程组的解是;那么方程组的解是 .
12. 已知x,y为实数,且 , 则的立方根是 .13. 已知关于的方程的解为 , 则一次函数与轴交点的坐标为 .14. 为了庆祝中国共产党成立100周年,某校举行“歌唱祖国”班级合唱比赛,评委将从“舞台造型、合唱音准和进退场秩序”这三项进行打分,各项成绩均按百分制计算,然后再按舞台造型占40%,合唱音准占40%,进退场秩序占20%计算班级的综合成锁.七(1)班三项成绩依次是95分、90分、95分,则七(1)班的综合成绩为 .15. 已知二元一次方程组的解是;那么方程组的解是 .三、解答题(共9题,共75分)
-
16. 计算:(1)、 ;(2)、 .17. 解下列方程组:(1)、(2)、18. 如图,有一架秋千,当它静止时,踏板离地的垂直高度 , 将它往前推送水平距离时,秋千的踏板离地的垂直高度 , 若秋干的绳索始终拉得很直,求绳索的长度.
 19. 如图,直线l是一次函数y=kx+b的图象,且经过点A(0,1)和点B(3,﹣2).
19. 如图,直线l是一次函数y=kx+b的图象,且经过点A(0,1)和点B(3,﹣2). (1)、求直线l的表达式;(2)、求直线l与两坐标轴所围成的三角形的面积.20. 如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
(1)、求直线l的表达式;(2)、求直线l与两坐标轴所围成的三角形的面积.20. 如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).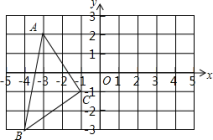
⑴在图中作出关于y轴对称的;
⑵写出点的坐标(直接写答案);
⑶在y轴上画出点P,使PB+PC最小.
21. 如图,在平面直角坐标系中,一次函数y=2x-3的图象分别交x轴,y轴于点A、B,将直线AB绕点B顺时针方向旋转45°,交x轴于点C,求直线BC的函数表达式.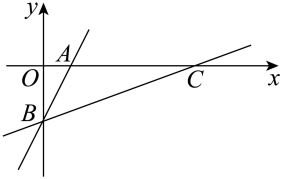 22. 某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的满分均为100分,前6名选手的得分如下:
22. 某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的满分均为100分,前6名选手的得分如下:序号
1号
2号
3号
4号
5号
6号
笔试成绩/分
85
92
84
90
84
80
面试成绩/分
90
88
86
90
80
85
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩.(综合成绩的满分仍为100分)
(1)、这6名选手笔试成绩的众数是分.(2)、现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比.(3)、求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.23. 习近平总书记说:“人民群众多读书,我们的民族精神就会厚重起来、深邃起来.”某书店计划在4月23日世界读书日之前,同时购进A,B两类图书,已知购进3本A类图书和4本B类图书共需288元;购进6本A类图书和2本B类图书共需306元.(1)、A,B两类图书每本的进价各是多少元?(2)、该书店计划用4500元全部购进两类图书,设购进A类x本,B类y本.①求y关于x的关系式;
②进货时,A类图书的购进数量不少于60本,已知A类图书每本的售价为38元,B类图书每本的售价为50元,求如何进货才能使书店所获利润最大,最大利润为多少元?