2022~2023学年中考数学一轮复习专题15图形折叠问题
试卷更新日期:2022-12-08 类型:一轮复习
一、直角三角形折叠问题
-
1. 如图,将三角形纸片 折叠,使点 、 都与点 重合,折痕分别为 、 .已知 , , ,则 的长为.
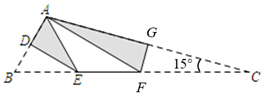 2. 如图,在 中, , , ,点E在线段 上,且 ,D是线段 上的一点,连接 ,将四边形 沿直线 翻折,得到四边形 ,当点G恰好落在线段 上时, .
2. 如图,在 中, , , ,点E在线段 上,且 ,D是线段 上的一点,连接 ,将四边形 沿直线 翻折,得到四边形 ,当点G恰好落在线段 上时, .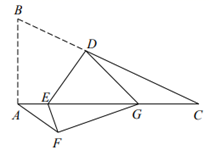 3. 如图,直角三角形 纸片中, ,点 是 边上的中点,连接 ,将 沿 折叠,点 落在点 处,此时恰好有 .若 ,那么 .
3. 如图,直角三角形 纸片中, ,点 是 边上的中点,连接 ,将 沿 折叠,点 落在点 处,此时恰好有 .若 ,那么 .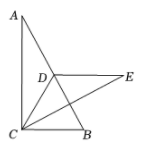 4. 如图,在 中, ,将边 沿 折叠,使点B落在 上的点 处,再将边 沿 折叠,使点A落在 的延长线上的点 处,两条折痕与斜边 分别交于点N、M , 则线段 的长为( )
4. 如图,在 中, ,将边 沿 折叠,使点B落在 上的点 处,再将边 沿 折叠,使点A落在 的延长线上的点 处,两条折痕与斜边 分别交于点N、M , 则线段 的长为( )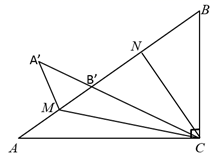 A、 B、 C、 D、5. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A、 B、 C、 D、5. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( ) A、 B、 C、 D、6. 如图1为一张正三角形纸片 , 其中点在上,点在上.今以为折线将点往右折后,、分别与相交于点、点,如图2所示.若 , , , , 则的长度为多少?( )
A、 B、 C、 D、6. 如图1为一张正三角形纸片 , 其中点在上,点在上.今以为折线将点往右折后,、分别与相交于点、点,如图2所示.若 , , , , 则的长度为多少?( )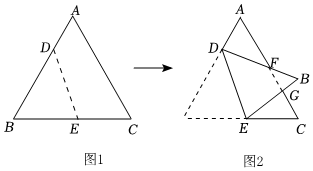 A、7 B、8 C、9 D、107. “做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片 , 第1次折叠使点落在边上的点处,折痕交于点;第2次折叠使点落在点处,折痕交于点.若 , 则.
A、7 B、8 C、9 D、107. “做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片 , 第1次折叠使点落在边上的点处,折痕交于点;第2次折叠使点落在点处,折痕交于点.若 , 则.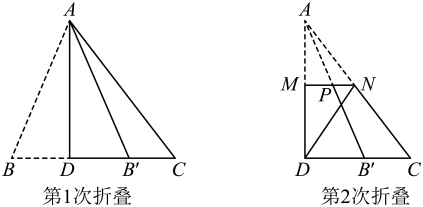 8. 如图,在△ABC中,∠ABC=40°, ∠ACB=90°,AE平分∠BAC交BC于点E.P是边BC上的动点(不与B,C重合),连结AP,将△APC沿AP翻折得△APD,连结DC,记∠BCD=α.
8. 如图,在△ABC中,∠ABC=40°, ∠ACB=90°,AE平分∠BAC交BC于点E.P是边BC上的动点(不与B,C重合),连结AP,将△APC沿AP翻折得△APD,连结DC,记∠BCD=α. (1)、如图,当P与E重合时,求α的度数.(2)、当P与E不重合时,记∠BAD=β,探究α与β的数量关系.9. 如图①,在 中, , , 是斜边 上的中线,点 为射线 上一点,将 沿 折叠,点 的对应点为点 .
(1)、如图,当P与E重合时,求α的度数.(2)、当P与E不重合时,记∠BAD=β,探究α与β的数量关系.9. 如图①,在 中, , , 是斜边 上的中线,点 为射线 上一点,将 沿 折叠,点 的对应点为点 .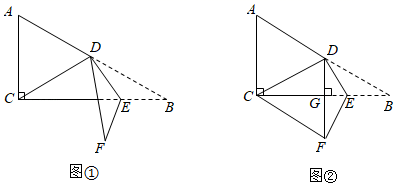 (1)、若 .直接写出 的长(用含 的代数式表示);(2)、若 ,垂足为 ,点 与点 在直线 的异侧,连接 ,如图②,判断四边形 的形状,并说明理由;(3)、若 ,直接写出 的度数.
(1)、若 .直接写出 的长(用含 的代数式表示);(2)、若 ,垂足为 ,点 与点 在直线 的异侧,连接 ,如图②,判断四边形 的形状,并说明理由;(3)、若 ,直接写出 的度数.二、矩形折叠问题(求角度)
-
10. 如图所示,将一矩形纸片沿AB折叠,已知 , 则( )
 A、48° B、66° C、72° D、78°11. 如图,在矩形纸片中, , , 将沿折叠到位置,交于点 , 则的值为( )
A、48° B、66° C、72° D、78°11. 如图,在矩形纸片中, , , 将沿折叠到位置,交于点 , 则的值为( )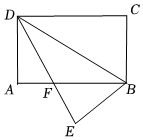 A、 B、 C、 D、12. 如图,矩形AOBC的顶点A、B在坐标轴上,点C的坐标是(﹣10,8),点D在AC上,将 BCD沿BD翻折,点C恰好落在OA边上点E处,则tan∠DBE等于( )
A、 B、 C、 D、12. 如图,矩形AOBC的顶点A、B在坐标轴上,点C的坐标是(﹣10,8),点D在AC上,将 BCD沿BD翻折,点C恰好落在OA边上点E处,则tan∠DBE等于( )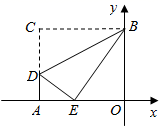 A、 B、 C、 D、13. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 、 ,若 , ,则 的度数是.
A、 B、 C、 D、13. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 、 ,若 , ,则 的度数是.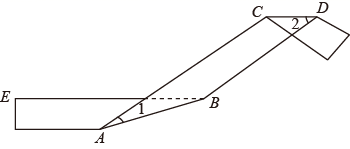 14. 如图,将矩形ABCD沿对角线AC折叠,点B的对应点为E,AE与CD交于点F.
14. 如图,将矩形ABCD沿对角线AC折叠,点B的对应点为E,AE与CD交于点F.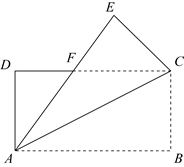 (1)、求证: ;(2)、若 ,求 的度数.
(1)、求证: ;(2)、若 ,求 的度数.三、矩形折叠问题(求定长)
-
15. 如图,在矩形纸片ABCD中,点E在BC边上,将 沿DE翻折得到 ,点F落在AE上.若 , ,则 cm.
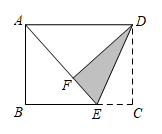 16. 如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .
16. 如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .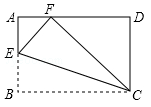 17. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .
17. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .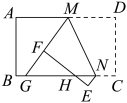 18. 矩形纸片中,E为的中点,连接 , 将沿折叠得到 , 连接.若 , , 则的长是( )
18. 矩形纸片中,E为的中点,连接 , 将沿折叠得到 , 连接.若 , , 则的长是( )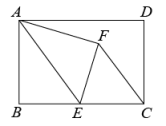 A、3 B、 C、 D、19. 如图,在矩形纸片ABCD中, , ,M是BC上的点,且 .将矩形纸片ABCD沿过点M的直线折叠,使点D落在AB上的点P处,点C落在点 处,折痕为MN,则线段PA的长是( )
A、3 B、 C、 D、19. 如图,在矩形纸片ABCD中, , ,M是BC上的点,且 .将矩形纸片ABCD沿过点M的直线折叠,使点D落在AB上的点P处,点C落在点 处,折痕为MN,则线段PA的长是( ) A、4 B、5 C、6 D、20. 如图,矩形纸片 , ,点 , 分别在 , 上,把纸片如图沿 折叠,点 , 的对应点分别为 , ,连接 并延长交线段 于点 ,则 的值为( )
A、4 B、5 C、6 D、20. 如图,矩形纸片 , ,点 , 分别在 , 上,把纸片如图沿 折叠,点 , 的对应点分别为 , ,连接 并延长交线段 于点 ,则 的值为( ) A、 B、 C、 D、21. 如图,将一张长方形纸片 沿 折叠,使 两点重合.点 落在点 处.已知 , .
A、 B、 C、 D、21. 如图,将一张长方形纸片 沿 折叠,使 两点重合.点 落在点 处.已知 , .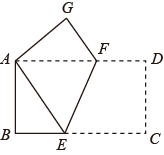 (1)、求证: 是等腰三角形;(2)、求线段 的长.22. 如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得 ,连接 ,当 时, 是以 为腰的等腰三角形.
(1)、求证: 是等腰三角形;(2)、求线段 的长.22. 如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得 ,连接 ,当 时, 是以 为腰的等腰三角形.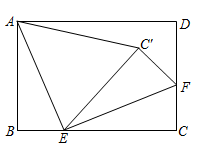 23. 如图,对折矩形纸片 , 使得与重合,得到折痕 , 把纸片展平,再一次折叠纸片,使点A的对应点落在上,并使折痕经过点B,得到折痕 . 连接 , 若 , , 则的长是 .
23. 如图,对折矩形纸片 , 使得与重合,得到折痕 , 把纸片展平,再一次折叠纸片,使点A的对应点落在上,并使折痕经过点B,得到折痕 . 连接 , 若 , , 则的长是 .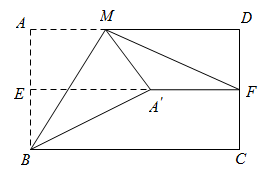
四、四边形折叠压轴问题(求最值)
-
24. 如图,有一张平行四边形纸片 , , , 将这张纸片折叠,使得点落在边上,点的对应点为点 , 折痕为 , 若点在边上,则长的最小值等于 .
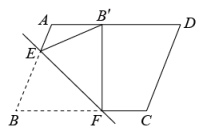 25. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动,连结CP , 点A关于直线CP的对称点为A′,连结A′C , A′P . 在运动过程中,点A′到直线AB距离的最大值是;点P到达点B时,线段A′P扫过的面积为 .
25. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动,连结CP , 点A关于直线CP的对称点为A′,连结A′C , A′P . 在运动过程中,点A′到直线AB距离的最大值是;点P到达点B时,线段A′P扫过的面积为 . 26. 如图,矩形ABCD中,AD=12,AB=8,E是AB上一点,且EB=3,F是BC上一动点,若将 沿EF对折后,点B落在点P处,则点P到点D的最短距为 .
26. 如图,矩形ABCD中,AD=12,AB=8,E是AB上一点,且EB=3,F是BC上一动点,若将 沿EF对折后,点B落在点P处,则点P到点D的最短距为 .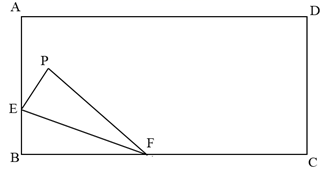
五、剪纸类折叠问题
-
27. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )
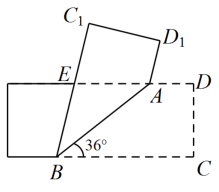
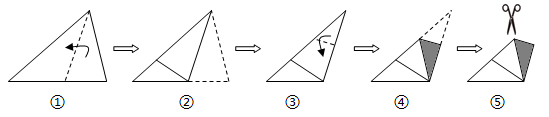 A、等腰三角形 B、直角三角形 C、矩形 D、菱形28. 小华用一张直角三角形纸片玩折纸游戏,如图1,在 中, , , .第一步,在 边上找一点 ,将纸片沿 折叠,点 落在 处,如图2,第二步,将纸片沿 折叠,点 落在 处,如图3.当点 恰好在原直角三角形纸片的边上时,线段 的长为.
A、等腰三角形 B、直角三角形 C、矩形 D、菱形28. 小华用一张直角三角形纸片玩折纸游戏,如图1,在 中, , , .第一步,在 边上找一点 ,将纸片沿 折叠,点 落在 处,如图2,第二步,将纸片沿 折叠,点 落在 处,如图3.当点 恰好在原直角三角形纸片的边上时,线段 的长为.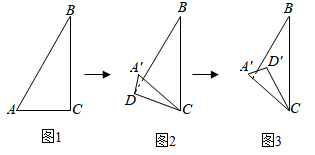 29. 如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到( )
29. 如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到( )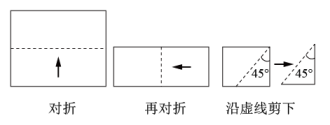 A、三角形 B、梯形 C、正方形 D、五边形30. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )
A、三角形 B、梯形 C、正方形 D、五边形30. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )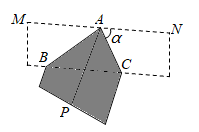 A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm231. 小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙), 的度数是.
A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm231. 小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙), 的度数是.
六、四边形折叠问题(其他)
-
32. 如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接 . 已知∠C=120°,∠BAE=50°,则的度数为( )
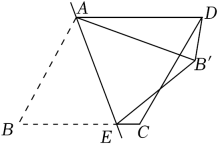 A、50° B、60° C、80° D、90°33. 如图,把一张矩形纸片沿对角线折叠,若BC=9,CD=3,那么阴影部分的面积为 .
A、50° B、60° C、80° D、90°33. 如图,把一张矩形纸片沿对角线折叠,若BC=9,CD=3,那么阴影部分的面积为 .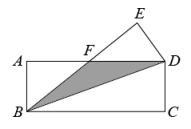 34. 如图,在四边形纸片中, , , . 将纸片折叠,使点落在边上的点处,折痕为 . 若 , 则的长为( )
34. 如图,在四边形纸片中, , , . 将纸片折叠,使点落在边上的点处,折痕为 . 若 , 则的长为( )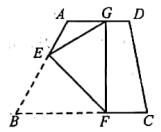 A、5 B、 C、 D、35. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .
A、5 B、 C、 D、35. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .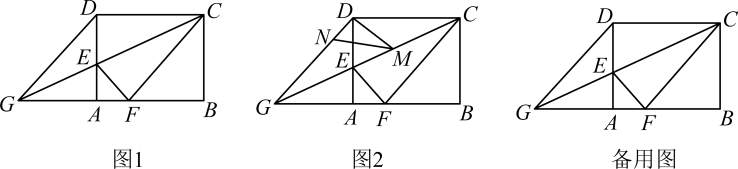 (1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.36. 将一个矩形纸片放置在平面直角坐标系中,点 , 点 , 点 , 点P在边上(点P不与点O,C重合),折叠该纸片,使折痕所在的直线经过点P,并与x轴的正半轴相交于点Q,且 , 点O的对应点落在第一象限.设 .
(1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.36. 将一个矩形纸片放置在平面直角坐标系中,点 , 点 , 点 , 点P在边上(点P不与点O,C重合),折叠该纸片,使折痕所在的直线经过点P,并与x轴的正半轴相交于点Q,且 , 点O的对应点落在第一象限.设 . (1)、如图①,当时,求的大小和点的坐标;(2)、如图②,若折叠后重合部分为四边形,分别与边相交于点E,F,试用含有t的式子表示的长,并直接写出t的取值范围;(3)、若折叠后重合部分的面积为 , 则t的值可以是(请直接写出两个不同的值即可).
(1)、如图①,当时,求的大小和点的坐标;(2)、如图②,若折叠后重合部分为四边形,分别与边相交于点E,F,试用含有t的式子表示的长,并直接写出t的取值范围;(3)、若折叠后重合部分的面积为 , 则t的值可以是(请直接写出两个不同的值即可).