2022~2023学年中考数学一轮复习专题14概率统计初步
试卷更新日期：2022-12-08 类型：一轮复习
一、数据收集和统计分析
-
1. 我国近十年的人口出生率及人口死亡率如图所示．
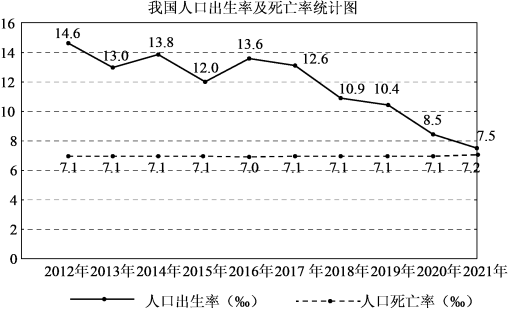
已知人口自然增长率=人口出生率—人口死亡率，下列判断错误的是（ ）
A、与2012年相比，2021年的人口出生率下降了近一半 B、近十年的人口死亡率基本稳定 C、近五年的人口总数持续下降 D、近五年的人口自然增长率持续下降2. 我市某校开展共创文明班，一起向未来的古诗文朗诵比赛活动，有10位同学参加了初赛，按初赛成绩由高到低取前5位进入决赛．如果小王同学知道了自己的成绩后，要判断能否进入决赛，他需要知道这10位同学成绩的（ ）A、平均数 B、众数 C、中位数 D、方差3. 期末考试后，办公室里有两位数学老师正在讨论他们班的数学考试成绩，邱老师：“我班的学生考得还不错，有一半的学生考90分以上，一半的学生考不到90分，”张老师：“我班大部分的学生都考在85分到90分之间，“依照上面两位老师所叙述的话你认为邱者师、张者师所说的话分别针对（ ）A、平均数、众数 B、中位数、众数 C、中位数、方差 D、平均数、中位数4. 小娅在对数据进行统计分析时，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果不受影响的统计量是（ ）A、平均数 B、中位数 C、方差 D、众数5. 下列说法正确的是（ ）A、为了解我国中小学生的睡眠情况，应采取全面调查的方式 B、一组数据1，2，5，5，5，3，3的众数和平均数都是3 C、若甲、乙两组数的方差分别是0.01，0.1，则甲组数据比乙组数据更稳定 D、抛掷一枚硬币200次，一定有100次“正面向上”6. 下列说法正确的是( )A、“打开电视剧，正在播足球赛”是必然事件 B、甲组数据的方差S甲2=0.24，乙组数据的方差S乙2=0.03，则乙组数据比甲组数据稳定 C、一组数据2，4，5，5，3，6的众数和中位数都是5 D、“掷一枚硬币正面朝上的概率是”表示每抛硬币2次就有1次正面朝上7. 在射击训练中，某队员的10次射击成绩如图，则这10次成绩的中位数和众数分别是（ ）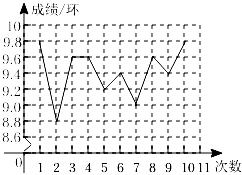
A、9.3，9.6 B、9.5，9.4 C、9.5，9.6 D、9.6，9.88. 第1组数据为：0、0、0、1、1、1，第2组数据为：、 ， 其中、是正整数．下列结论：①当时，两组数据的平均数相等；②当时，第1组数据的平均数小于第2组数据的平均数；③当时，第1组数据的中位数小于第2组数据的中位数；④当时，第2组数据的方差小于第1组数据的方差．其中正确的是（ ）A、①② B、①③ C、①④ D、③④二、有关概率求解问题
-
9. 为扎实推进“五育并举”工作，某校利用课外活动时间开设了舞蹈、篮球、围棋和足球四个社团活动，每个学生只选择一项活动参加．为了解活动开展情况，学校随机抽取部分学生进行调查，将调查结果绘成如下表格和扇形统计图．
参加四个社团活动人数统计表
社团活动
舞蹈
篮球
围棋
足球
人数
50
30
80
参加四个社团活动人数扇形统计图
请根据以上信息，回答下列问题：
(1)、抽取的学生共有人，其中参加围棋社的有人；(2)、若该校有3200人，估计全校参加篮球社的学生有多少人？(3)、某班有3男2女共5名学生参加足球社，现从中随机抽取2名学生参加学校足球队，请用树状图或列表法说明恰好抽到一男一女的概率．10. 教育部在《大中小学劳动教育指导纲要（试行）》中明确要求：初中生每周课外生活和家庭生活中，劳动时间不少于3小时．某走读制初级中学为了解学生劳动时间的情况，对学生进行了随机抽样调查，并将调查结果制成不完整的统计图表，如图：平均每周劳动时间的频数统计表
劳动时间小时
频数
t＜3
9
3≤t＜4
a
4≤t＜5
66
t≥5
15
请根据图表信息，回答下列问题．
(1)、参加此次调查的总人数是人，频数统计表中a＝；(2)、在扇形统计图中，D组所在扇形的圆心角度数是°；(3)、该校准备开展以“劳动美”为主题的教育活动，要从报名的2男2女中随机挑选2人在活动中分享劳动心得，请用树状图或列表法求恰好抽到一名男生和一名女生的概率．11. 某学校为满足学生多样化学习需求，准备组建美术、劳动、科普、阅读四类社团．学校为了解学生的参与度，随机抽取了部分学生进行调查，将调查结果绘制成如图所示的不完整的统计图．请根据图中的信息，解答下列问题：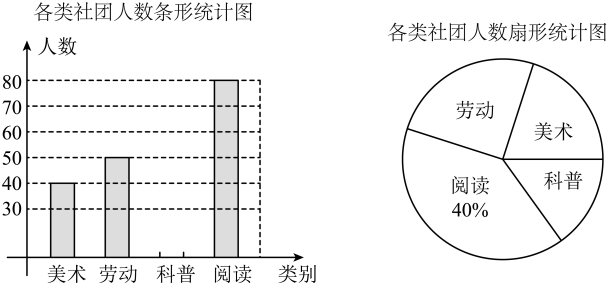
(1)、求本次调查的学生人数，并补全条形统计图；(2)、若全校共有学生3600人，求愿意参加劳动类社团的学生人数；(3)、甲、乙两名同学决定在阅读、美术、劳动社团中选择参加一种社团，请用树状图或列表法表示出所有等可能结果，并求出恰好选中同一社团的概率．12. 宁夏某枸杞育种改良试验基地对新培育的甲、乙两个品种各试种一亩，从两块试验地中各随机抽取10棵，对其产量（千克/棵）进行整理分析．下面给出了部分信息：甲品种：2.0，3.2，3.1，3.2，3.1，2.5，3.2，3.6，3.8，3.9
乙品种：如图所示
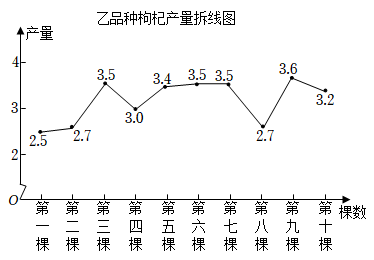
平均数
中位数
众数
方差
甲品种
3.16
3.2
0.29
乙品种
3.16
3.3
0.15
根据以上信息，完成下列问题：(1)、填空： ， ；(2)、若乙品种种植棵，估计其产量不低于千克的棵数；(3)、请从某一个方面简要说明哪个品种更好．13. 某市教育局为了解“双减”政策落实情况，随机抽取几所学校部分初中生进行调查，统计他们平均每天完成作业的时间，并根据调查结果绘制如下不完整的统计图：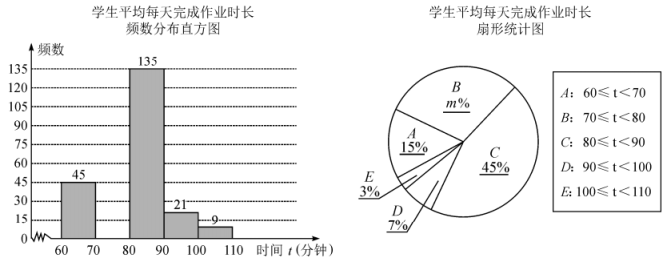
请根据图表中提供的信息，解答下面的问题：
(1)、在调查活动中，教育局采取的调查方式是（填写“普查”或“抽样调查”）；(2)、教育局抽取的初中生有人，扇形统计图中m的值是；(3)、已知平均每天完成作业时长在“”分钟的9名初中生中有5名男生和4名女生，若从这9名学生中随机抽取一名进行访谈，且每一名学生被抽到的可能性相同，则恰好抽到男生的概率是；(4)、若该市共有初中生10000名，则平均每天完成作业时长在“”分钟的初中生约有人.14. 为了从甲、乙两位同学中选拔一人参加知识竞赛，举行了6次选拔赛，根据两位同学6次选拔赛的成绩，分别绘制了如图统计图．
(1)、填写下列表格平均数/分
中位数/分
众数/分
甲
90
①
93
乙
②
87.5
③
(2)、如果分别从甲、乙两人的6次成绩中各随机抽取一次成绩进行分析，求抽到的两个人的成绩都不低于90分的概率．三、事件发生可能性估计
-
15. 下列说法正确的是（ ）A、是无理数 B、明天巴中城区下雨是必然事件 C、正五边形的每个内角是 D、相似三角形的面积比等于相似比16. 在某市组织的物理实验操作考试中，考试所用实验室共有24个测试位，分成6组，同组4个测试位各有一道相同试题，各组的试题不同，分别标记为A，B，C，D，E，F，考生从中随机抽取一道试题，则某个考生抽到试题A的概率为（ ）A、 B、 C、 D、17. 如图，一张圆桌共有3个座位，甲、乙，丙3人随机坐到这3个座位上，则甲和乙相邻的概率为（ ）
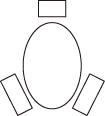A、 B、 C、 D、18. 下列事件是必然事件的是（ ）A、三角形内角和是180° B、端午节赛龙舟，红队获得冠军 C、掷一枚均匀骰子，点数是6的一面朝上 D、打开电视，正在播放神舟十四号载人飞船发射实况19. 下列说法中，正确的是（ ）A、调查某班45名学生的身高情况宜采用全面调查 B、“太阳东升西落”是不可能事件 C、为了直观地介绍空气各成分的百分比，最适合使用的统计图是条形统计图 D、任意投掷一枚质地均匀的硬币26次，出现正面朝上的次数一定是13次20. 将一副去掉大小王的扑克牌平均分发给甲、乙、丙、丁四人，已知甲有5张红桃牌，乙有4张红桃牌，那么丁的红桃牌有种不同的情况．21. 一个盒子中装有 个红球和若干个白球，这些求除颜色外都相同，再往该盒子中放入 个相同的白球，摇匀后从中随机摸出一个球，若摸到白球的概率为 ，则盒子中原有的白球的个数为.
或 
），如正北方向的卦为 
.从图中三根线组成的卦中任取一卦，这一卦中恰有2根 
