2022-2023学年华师大版数学八年级上学期期末模拟试卷

试卷更新日期：2022-12-08 类型：期末考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列说法正确的是（）

A、﹣27的立方根是3 B、 $\sqrt{16}$ ＝±4 C、1的平方根是1 D、4的算术平方根是2

查看试题解析
2. 下列计算正确的是（）

A、a²+a²=a⁴ B、a⁵•a²=a⁷ C、（a²）³=a⁵ D、2a²﹣a²=2

查看试题解析
3. 下列四个多项式中，可以分解因式的是（）

A、 $x^{2} + x$ B、 $x^{2} - 4 x + 8$ C、 $x^{2} + 2 y + 1$ D、 $x^{2} - 4 y^{3}$

查看试题解析
4. 已知 $(x + 3) (x - 2) = x^{2} + b x + c$ ，那么 $b$ 、 $c$ 的值分别是（）

A、 $b = 1$ ， $c = - 6$ B、 $b = 1$ ， $c = 6$ C、 $b = 5$ ， $c = - 6$ D、 $b = 5$ ， $c = 6$

查看试题解析
5. 如图，数轴上点A、B、C分别对应 $1$ 、 $2$ 、 $3$ ，过点 $C$ 作 $P Q ⊥ A B$ ，以点C为圆心， $B C$ 长为半径画弧，交 $P Q$ 于点D，以点A为圆心， $A D$ 长为半径画弧，交数轴于点M，则点M对应的数是（）

A、 $\sqrt{3} + 1$ B、 $\sqrt{5} + 1$ C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
6. 如图所示，将如图一所示的大小相同的四个小正方形按图二所示的方式放置在一个边长为a的大正方形中，中间恰好空出两条互相垂直的宽都为b的长方形，根据图二中阴影部分的面积计算方法可以验证的公式为（）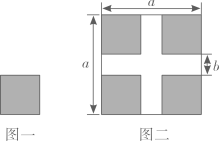

A、（a+b）（a﹣b）＝a²﹣b² B、（a+b）²＝a²+2ab+b² C、（a﹣b）²＝a²﹣2ab+b² D、（a﹣b）²＝（a+b）²﹣4ab

查看试题解析
7. 如图，点E在 $A C$ 上， $△ A B C ≌ △ D A E$ ， $B C = 3$ ， $D E = 7$ ，则 $C E$ 的长为（）

A、2 B、3 C、4 D、5

查看试题解析
8. 有40个数据，共分成6组，第1~4组的频数分别为10、5、7、6，第5组的频率是0. 1，则第6组的频率是（）

A、0. 2 B、0. 3 C、0. 1 D、0. 4

查看试题解析
9. 如图， $D E$ 是 $Δ A B C$ 中 $A C$ 边的垂直平分线，交 $B C$ 于点 $D$ ，交 $A C$ 于点 $E$ ，若 $B C = 8 c m$ ， $A D = 5 c m$ ，则 $B D$ 的长为（）

A、 $3 c m$ B、 $4 c m$ C、 $5 c m$ D、 $6 c m$

查看试题解析
10. 如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D'处，若AB=3，AD=4，则ED的长为（）

A、 $\frac{3}{2}$ B、3 C、1 D、 $\frac{4}{3}$

查看试题解析

二、填空题（每题3分，共15分）

11. 计算： $\sqrt{8} + {(- 1)}^{2020} - | - \sqrt{2} | =$ .

查看试题解析
12. 在实数范围内因式分解： $2 x^{2} - 4 x + 1 =$ .

查看试题解析
13. $(2 x + 3 y + 5) (2 x + 3 y - 5) =$ ．

查看试题解析
14. 如图， $A D$ 是 $△ A B C$ 的角平分线， $∠ C = 90^{\circ} ， C D = 3 cm$ ，点P是 $A B$ 上一动点，连接 $D P$ ，则 $D P$ 的最小值为cm，.

查看试题解析
15. 在Rt△ABC中，AC＝8，BC＝6，∠C＝90°．现将△ABC按如图那样折叠，使点A与点B重合，折痕为DE，则DE的长为．

查看试题解析

三、解答题（共8题，共75分）

16. 计算： $\sqrt[3]{8} - \sqrt{4} - \sqrt{{(- 3)}^{2}} + | 1 - \sqrt{2} |$ .

查看试题解析
17. 化简：

(1)、 ${(2 x^{3} y)}^{2} \cdot (- 2 x y) + {(- 2 x^{3} y)}^{3} \div (2 x^{2})$

(2)、[(a－2b)²＋(a－2b)(2b＋a)－2a(2a－b)]÷2a.

查看试题解析
18. 已知某正数的两个平方根分别是a-3和2a+15，b的立方根是-3，求a-b的值．

查看试题解析
19. 已知 $a 、 b 、 c$ 是三边 $Δ A B C$ 的长，且满足 $a^{2} + b^{2} + c^{2} + 50 = 6 a + 8 b + 10 c$ ，求 $Δ A B C$ 三边的长.

查看试题解析
20. 如图， $A B$ 、 $C D$ 相交于点 $O$ ， $A C = B D$ ， $A E ⊥ C D$ 于点 $E$ ， $B F ⊥ C D$ 于点 $F$ ，且 $C E = D F$ ．
求证： $A C ∥ B D$ ．

查看试题解析
21. 如图，铁路上A，B两点相距25km，C，D为两村庄， $D A ⊥ A B$ 于点A， $C B ⊥ A B$ 于点B，若 $D A = 10 k m$ ， $C B = 15 k m$ ，现要在AB上建一个周转站E，使得C，D两村到E站的距离相等，则周转站E应建在距A点多远处？

查看试题解析
22. 2013年起，深圳市实施行人闯红灯违法处罚，处罚方式分为四类：“罚款20元”“罚款50元”“罚款100元”、“穿绿马甲维护交通”.下图是实施首日由某片区的执法结果整理数据后绘制的两幅不完整的统计图.
请你根据图中提供的信息，解答下列问题：

根据图中提供的信息，解答下列问题：

(1)、实施首日，该片区行人闯红灯违法受处罚一共人.

(2)、在所有闯红灯违法受处罚的行人中，穿绿马甲维护交通所占的百分比是%；

(3)、据了解，“罚款20元”人数是“罚款50元”人数的2倍，请补全条形统计图；

(4)、根据（3）中的信息，在扇形统计图中，“罚款20元”所在扇形的圆心角等于度.（写出计算过程）

查看试题解析
23. 综合与实践
某学校的数学兴趣小组发现这样一个模型，两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来，会形成一组全等的三角形，具有这个规律的图形称为“手拉手”图形．

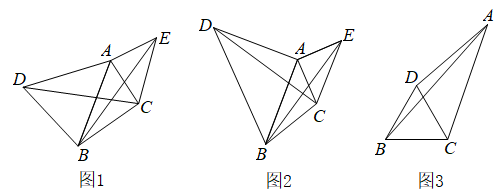(1)、[材料理解]如图1，在 $△ A B C$ 中，分别以 $A B$ ， $A C$ 为边向外作等腰 $△ A B D$ 和等腰 $△ A C E$ ． $A B ＝ A D$ ， $A C ＝ A E$ ， $∠ B A D = ∠ C A E$ ，连接 $B E$ ， $C D$ ，试猜想 $B E$ 与 $C D$ 的大小关系，并说明理由；

(2)、[深入探究]如图2，在 $△ A B C$ 中， $A B ＝ 6$ ， $B C ＝ 4$ ， $∠ A B C ＝ 45 °$ ，分别以 $A B$ ， $A C$ 为边向外作等腰直角 $△ A B D$ 和等腰直角 $△ A B C$ ， $∠ B A D ＝ ∠ C A E ＝ 90 °$ ，连接 $B E$ ， $C D$ ，求 $B E$ 的长．

(3)、[延伸应用]如图3，在 $△ A B C$ 中， $A B ＝ 10$ ，点D为平面内一点，连接 $A D$ ， $B D$ ，满足 $A D ＝ 6$ ， $B D ＝ B C$ ， $∠ D B C ＝ 60 °$ ， $∠ D A C ＝ 30 °$ ，求 $A C$ 的长．

查看试题解析