（苏科版）2022-2023学年九年级数学下册6.7 用相似三角形解决问题 同步测试
试卷更新日期：2022-12-08 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在外选一点C，在、上分别找点M，N，使得 ， ， 测量出的长为 ， 由此可知A、B间的距离为（ ）
A、 B、 C、 D、2. 如图，AB是斜靠在墙上的梯子，梯脚距墙2米，梯子上的点D距墙1.8米，BD长0.6米，则梯子的长为（ ）
A、5.6米 B、6米 C、6.1米 D、6.2米3. 我国古代数学著作《九章算术》中的“井深”问题：“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”，它的题意是：如图尺，尺，问井深是多少．如图，设井深为x尺，所列方程正确的是（ ）
A、 B、 C、 D、4. 如图，有一块锐角三角形材料，边BC＝120mm ， 高AD＝90mm ， 要把它加工成矩形零件，使其一边在BC上，其余两个顶点分别在AB ， AC ， 且EH＝2EF ， 则这个矩形零件的长为（ ）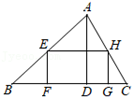
A、36mm B、80mm C、40mm D、72mm5. 西周数学家商高总结了用“矩”（如图1）测量物高的方法：把矩的两边放置成如图2的位置，从矩的一端A（人眼）望点E，使视线通过点C，记人站立的位置为点B，量出BG长，即可算得物高EG．令BG=x（m）， EG=y（m），若a=30cm，b=60cm，AB=1.6m，则y关于x的函数表达式为（ ）
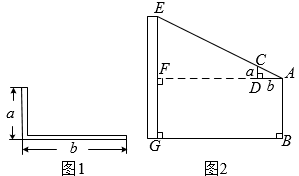A、 B、 C、 D、6. 如图，在中， ， ， 点、分别在、上， ， ， 交于点 ， 则面积的最大值是（ ）
A、2 B、3 C、4 D、57. 如图，在一张台球桌上，一球在点A处，要从A处击打出去，经球台边挡板CD反射击中B球．作AC⊥CD于点C，BD⊥CD于点D．已知∠AEC＝∠BED，AC＝10cm，BD＝15cm，CD＝20cm，若球手恰好能击中B球，则DE的长为（ ）
A、8cm B、10cm C、12cm D、cm8. “跳眼法”是指用手指和眼睛估测距离的方法步骤：
第一步：水平举起右臂，大拇指紧直向上，大臂与身体垂直；
第二步：闭上左眼，调整位置，使得右眼、大拇指、被测物体在一条直线上；
第三步：闭上右眼，睁开左眼，此时看到被测物体出现在大拇指左侧，与大拇指指向的位置有一段横向距离，参照被测物体的大小，估算横向距离的长度；
第四步：将横向距离乘以10（人的手臂长度与眼距的比值一般为10），得到的值约为被测物体离观测，点的距离值．
如图是用“跳眼法”估测前方一辆汽车到观测点距离的示意图，该汽车的长度大约为4米，则汽车到观测点的距离约为（ ）
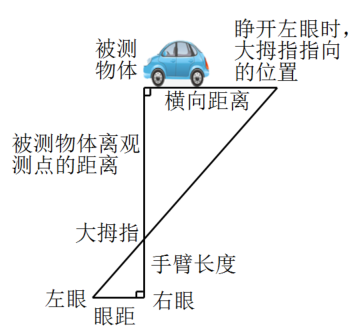A、40米 B、60米 C、80米 D、100米9. 在设计人体雕像时，使雕像上部（腰部以上）与下部（腰部以下）的高度比，等于下部与全部的高度比，可以增加视觉美感.如图，按此比例设计一座高度为2m 的雷锋雕像，那么该雕像的下部设计高度约是（ ）（结果精确到 .参考数据： ， ， ）
A、 B、 C、 D、10. 如图，有座塔在河流北岸的点E处，一棵树位于河流南岸的点A处，从点A处开始，在河流南岸立4根标杆，以这4根标杆为顶点，组成边长为10米的正方形ABCD，且A，D，E三点在一条直线上，在标杆B处观察塔E，视线BE与边DC相交于点F，如果测得米，那么塔与树的距离AE为（ ）
A、15米 B、20米 C、25米 D、30米二、填空题（每题3分，共15分）
-
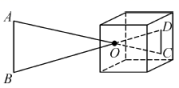
11. 如图是小孔成像原理的示意图， ， ， . 若物体的高度为 ， 则像的高度是.
12. 为了测量河宽AB，有如下方法：如图，取一根标尺CD横放，使CD∥AB，并使点B，D，O和点A，C，O分别在同一条直线上，量得CD＝15米，OC＝10米，AC＝20米，则河宽AB的长度为米.
13. 如图是某风车示意图，其相同的四个叶片均匀分布，水平地面上的点M在旋转中心O的正下方，某一时刻，太阳光线恰好垂直照射叶片、 ， 此时各叶片影子在点M右侧成线段 ． 测得 ， ， 垂直于地面的木棒与影子的比为 ． 则点O、M之间的距离等于m；
14. 如图，利用标杆DE测量楼高，点A、D、B在同一条直线上，DE⊥AC，BC⊥AC，垂足分别为E、C．若测得AE＝1m，DE＝1.5m，CE＝5m，则楼高BC为m．
15. 据《墨经》记载，在两千多年前，我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验，阐释了光的直线传播原理，如图（1）所示。如图（2）所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是6cm，则蜡烛火焰的高度是cm．
三、解答题（共3题，共15分）
-
16. 如图所示，某校数学兴趣小组利用标杆BE测量建筑物的高度．已知标杆BE的高为1m，测得AB＝2m，AC＝10m，求建筑物CD的高.
17. 如图，小欣站在灯光下，投在地面上的身影 ， 蹲下来，则身影 ， 已知小明的身高 ， 蹲下时的高度等于站立高度的一半，求灯离地面的高度 ．
18. 如图所示，某测量工作人员头顶A与标杆顶点F、电视塔顶端E在同一直线上，已知此人眼睛距地面AB的长为1.6m ， 标杆FC的长为3.2m ， 且BC的长为2m ， CD的长为5m ， 求电视塔的高ED ．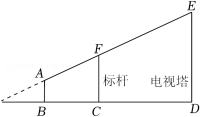
四、综合题（共5题，共40分）
-
19. 如图，阳光下，小亮的身高如图中线段AB所示，他在地面上的影子如图中线段BC所示，线段DE表示旗杆的高，线段FG表示一堵高墙
(1)、请你在图中画出旗杆在同一时刻阳光照射下形成的影子的示意图；(2)、如果小亮的身高 ， 他的影子 ， 旗杆的高 ， 旗杆与高墙的距离 ， 请求出旗杆的影子落在墙上的长度.20.如图，身高1.6米的小明从距路灯的底部（点O）20米的点A沿AO方向行走14米到点C处，小明在A处，头顶B在路灯投影下形成的影子在M处．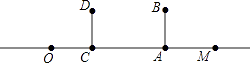
(1)、已知灯杆垂直于路面，试标出路灯P的位置和小明在C处，头顶D在路灯投影下形成的影子N的位置．(2)、若路灯（点P）距地面8米，小明从A到C时，身影的长度是变长了还是变短了？变长或变短了多少米？21. 如图，一路灯与墙相距20米，当身高米的小亮在离墙17米的D处时，影长为1米．
(1)、求路灯B的高度；(2)、若点P为路灯，请画出小亮位于N处时，在路灯P下的影子NF（用粗线段表示出来）22. 如图1，平直的公路旁有一灯杆 ， 在灯光下，小丽从灯杆的底部处沿直线前进到达点，在处测得自己的影长小丽身高 ．
(1)、求灯杆的长；(2)、若小丽从处继续沿直线前进到达处（如图2），求此时小丽的影长的长．23. 如图，公路旁有两个高度相等的路灯AB、CD，小明上午上学时发现路灯AB在太阳光下的影子恰好落在路牌底部E处，他自己的影子恰好落在路灯CD的底部C处；晚自习放学时，站在上午同一个地方，发现在路灯CD的灯光下自己的影子恰好落在E处．
(1)、在图中画出小明的位置(用线段FG表示)．(2)、若上午上学时，高1米的木棒的影子为2米，小明身高为1.5米，他距离路牌底部E恰好2米，求路灯高．