北师大版数学八年级上册《 第七章 平行线的证明》期末高分突破卷
试卷更新日期:2022-12-07 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 下列命题中,真命题是
 ( ) A、两个锐角的和一定是钝角 B、相等的角是对顶角 C、一个三角形中至少有两个锐角 D、带根号的数一定是无理数2. 下列语句是命题的是( )A、画出两个相等的角 B、所有的直角都相等吗 C、延长线段到C,使得 D、两直线平行,内错角相等3. 在中,若 , 则的度数为( )A、 B、 C、 D、4. 如图,下列条件中,一定能判断的是( )
( ) A、两个锐角的和一定是钝角 B、相等的角是对顶角 C、一个三角形中至少有两个锐角 D、带根号的数一定是无理数2. 下列语句是命题的是( )A、画出两个相等的角 B、所有的直角都相等吗 C、延长线段到C,使得 D、两直线平行,内错角相等3. 在中,若 , 则的度数为( )A、 B、 C、 D、4. 如图,下列条件中,一定能判断的是( )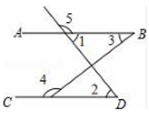 A、 B、 C、 D、5. 如图,点E在AB的延长线上,下列条件中能够判断AD∥BC的是( )
A、 B、 C、 D、5. 如图,点E在AB的延长线上,下列条件中能够判断AD∥BC的是( ) A、∠1=∠3 B、∠C=∠CBE C、∠C+∠ABC=180° D、∠2=∠46. 如图,点B是△ADC的边AD的延长线上一点,DE∥AC, 若∠C=50°,∠BDE=60°,则∠CDB的度数等于( )
A、∠1=∠3 B、∠C=∠CBE C、∠C+∠ABC=180° D、∠2=∠46. 如图,点B是△ADC的边AD的延长线上一点,DE∥AC, 若∠C=50°,∠BDE=60°,则∠CDB的度数等于( ) A、70° B、100° C、110° D、120°7. 如图,能判定EC∥AB的条件是( )
A、70° B、100° C、110° D、120°7. 如图,能判定EC∥AB的条件是( ) A、∠B=∠ACE B、∠A=∠ECD C、∠B=∠ACB D、∠A=∠ACE8. 如图,若ABEF,AE=AC,∠E=65°,则∠CAB的度数为( )
A、∠B=∠ACE B、∠A=∠ECD C、∠B=∠ACB D、∠A=∠ACE8. 如图,若ABEF,AE=AC,∠E=65°,则∠CAB的度数为( ) A、25° B、50° C、60° D、65°9. 如图, , , 平分 , 平分 , 则( )
A、25° B、50° C、60° D、65°9. 如图, , , 平分 , 平分 , 则( )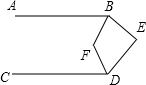 A、 B、 C、 D、10. 如图,是的角平分线,的垂直平分线分别交于 , 交的延长线于K,连接 , 则下列结论:①;②;③;④.其中正确的结论有( )
A、 B、 C、 D、10. 如图,是的角平分线,的垂直平分线分别交于 , 交的延长线于K,连接 , 则下列结论:①;②;③;④.其中正确的结论有( ) A、①③ B、①②③ C、②③④ D、①②③④
A、①③ B、①②③ C、②③④ D、①②③④二、填空题(每题3分,共15分)
-
11. 如图所示,用直尺和三角尺作直线AB∥CD,这种作法的依据是.
 12. 在△ABC中,∠A+∠B=90° ,则△ABC是三角形。13. 请举反例说明命题“若 , 则”是假命题,你举的反例是 .14. 如图,直线a,b被直线c,d所截。若a∥b,∠1=120°,∠2=30°,则∠3=.
12. 在△ABC中,∠A+∠B=90° ,则△ABC是三角形。13. 请举反例说明命题“若 , 则”是假命题,你举的反例是 .14. 如图,直线a,b被直线c,d所截。若a∥b,∠1=120°,∠2=30°,则∠3=. 15. 将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为 .
15. 将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为 .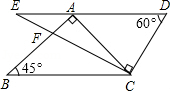
三、解答题(共8题,共75分)
-
16. 如图,AF=DB,BC=EF,AC=ED,求证:CB∥EF.
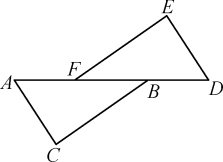 17. 如图,CD是∠ACB的角平分线,DE∥BC,∠AED=70°,求∠EDC的度数.
17. 如图,CD是∠ACB的角平分线,DE∥BC,∠AED=70°,求∠EDC的度数. 18. 如图,在中, , , CD是的高线,CE是的角平分线,求的度数.
18. 如图,在中, , , CD是的高线,CE是的角平分线,求的度数. 19. 如图,在中, , 的垂直平分线交于点D,交于点E, , 求的度数和边的长.
19. 如图,在中, , 的垂直平分线交于点D,交于点E, , 求的度数和边的长. 20. 如图,已知 , , , 求证:ab.
20. 如图,已知 , , , 求证:ab.

