北师大版数学八年级上册《 第六章 数据的分析》期末高分突破卷
试卷更新日期：2022-12-07 类型：复习试卷
一、单选题（每题3分，共30分）
-
1. 小雨同学参加了学校举办的“抗击疫情，你我同行”主题演讲比赛，她的演讲内容语言表达和形象风度三项得分分别为80分，90分，85分，若这三项依次按照50%，30%，20%的百分比确定成绩，则她的成绩是（ ）A、82分 B、83分 C、84分 D、85分2. 一组数据x、0、1、﹣2、3的平均数是1，则这组数据的中位数是（ ）A、0 B、1 C、2.5 D、33. 某次射击比赛，甲队员的成绩如图，根据此统计图，下列结论中错误的是（ ）
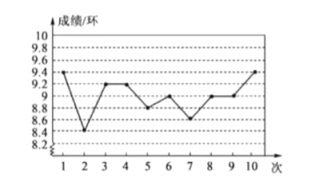A、最高成绩是9.4环 B、平均成绩是9环 C、这组成绩的众数是9环 D、这组成绩的方差是8.74. 甲、乙两名运动员在相同的条件下，各射击10次，经过计算，甲、乙两人成绩的平均数均是9.5环，甲的成绩的方差是0.125，乙的成绩的方差是1.85，那么这10次射击中，甲、乙成绩的稳定情况是（ ）A、甲较为稳定 B、乙较为稳定 C、两个人成绩一样稳定 D、不能确定5. 快要到新年了，某鞋店老板要进一批新年鞋，他一定会参考下面的调查数据，他最关注的是（ ）A、中位数 B、平均数 C、加权平均数 D、众数6. 乒乓球是我国的国球，也是世界上流行的球类体育项目.我国乒乓球名将与其对应身高如下表所示：乒乓球名将
刘诗雯
邓亚萍
白杨
丁宁
陈梦
孙颖莎
姚彦
身高（ ）
160
155
171
173
163
160
175
这些乒乓球名将身高的中位数和众数是（ ）
A、160，163 B、173，175 C、163，160 D、172，1607. 八年级（1）班30名学生的身高情况如下表：身高（m）
1.45
1.48
1.50
1.53
1.55
1.65
1.70
人数
x
y
6
8
5
3
1
关于身高的统计量中，不随x、y的变化而变化的有（ ）
A、众数，中位数 B、中位数，方差 C、平均数，方差 D、平均数，众数8. 如果与的平均数是5，那与的平均数是（ ）A、4 B、5 C、6 D、79. 甲、乙、丙、丁四位同学都参加了5次数学模拟测试，每个人这5次成绩的平均数都是92分，方差分别是 ， ， ， ， 则这5次测试成绩最稳定的是（ ）A、甲 B、乙 C、丙 D、丁10. 小明在七年级第二学期的数学成绩如下表．如果按如图所示的权重计算总评得分，那么小明该学期的总评得分为（ ）姓名
平时
期中
期末
总评
小明
90
90
85
A、86分 B、87分 C、88分 D、89分二、填空题（每题3分，共15分）
-
11. 学校运动会上，共有15名同学参加了男子100米预赛，参赛选手要想知道自己是否能进入前8名，从而取得决赛资格，只需要了解自己的成绩以及全部成绩的 ．12. 甲、乙两地7月上旬的日平均气温如图所示，则甲，乙两地这10天中日平均气温的方差S2甲与S2乙的大小关系是S2甲S2乙 ． （填“＞”或“＜”）
13. 某博物馆拟招聘一名优秀讲解员，其中小林笔试、试讲、面试三轮测试得分分别为92分，80分、85分．综合成绩中笔试占50%、试讲占30%、面试占20%，那么小林的最后得分为分．14. 某品牌专卖店9月份销售了20双运动鞋，其尺码和数量统计如下表：尺码
38
39
40
41
42
数量
2
4
5
6
3
这20双运动鞋尺码的众数是 ．
15. 用 计算一组数据的方差，那么x1+x2+x3…+x8＝.三、解答题（共8题，共75分）
-
16. 某校学生会决定从甲、乙两名学生会干事中选拔一名副主席，选拔包括笔试、面试和民主测评三项，每项得分依次按4：4：2的比例确定个人的最终得分，甲、乙两名候选人的三项成绩如下表所示：
测试项目
测试成绩/分
甲
乙
笔试
80
90
面试
70
70
民主测评
80
70
请通过计算说明哪位同学最终得分高？
17. 下面的条形统计图描述了某车间20个工人日加工零件数的情况，求这些工人日加工零件数的众数、中位数、平均数．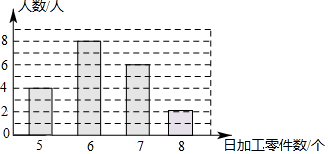
18. 某公司对甲、乙两名应聘者进行面试，并按专业知识、工作经验和仪表形象三项给应聘者打分，每项满分20分，打分结果如下表（单位：分）：专业知识
工作经验
仪表形象
甲
14
18
12
乙
18
16
11
根据实际需要，公司将专业知识、工作经验和仪表形象三项得分按6∶3∶1的比确定应聘者的最终成绩，那么应该录用谁？请说明理由．
19. 某农业科技部门为了解甲、乙两种新品西瓜的品质（大小、甜度等），进行了抽样调查，在相同条件下，随机抽取了两种西瓜各7份样品，对西瓜的品质进行评分（百分制），并对数据进行收集、整理，得到两种西瓜得分的统计图：
对数据进行分析，得到如下统计量：
平均数
中位数
众数
方差
甲种西瓜
88
88
96
44.86
乙种西瓜
88
90
90
21.43
请根据以上信息分析哪种西瓜的品质更好，并说明理由.
20. 在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：
（Ⅰ）图1中a的值为 ▲ ；
（Ⅱ）求统计的这组初赛成绩数据的平均数、众数和中位数；
（Ⅲ）根据这组初赛成绩，由高到低确定9人进入复赛，请直接写出初赛成绩为1.65m的运动员能否进入复赛．
21. 某单位欲从内部招聘管理人员一名，对甲、乙、丙三名候选人进行了笔试和面试两项测试，三人的测试成绩如下表所示：
根据录用程序，组织200名职工对三人利用投票推荐的方式进行民主评议，三人得票率（没有弃权票，每位职工只能推荐1人）如上图所示，每得一票记作1分．
(1)、请算出三人的民主评议得分；(2)、如果根据三项测试的平均成绩确定录用人选，那么谁将被录用（精确到 0.01 )?(3)、根据实际需要，单位将笔试、面试、民主评议三项测试得分按 4 ： 3 ： 3 的比例确定个人成绩，那么谁将被录用？22. 为落实“双减”政策，满足学生课后延时服务需求，某校以课后服务“5+2”的模式全面开展内容丰富、形式多样的活动，切实减轻学生学习负担，促进学生健康成长．为了了解八年 级学生延时时间范围内的体育活动情况，某调查小组随机从八年 级学生中抽取了 30 名男同学，20 名女同学进行了为期一周的跟踪调查，调查结果如表所示：
性别
平均每天参加体育活动达到1 小时的人数
平均每天参加体育活动不达1 小时的人数
合计
男生
25
5
30
女生
11
m
20
合计
36
14
50
对平均每天参加体育活动达到 1 小时的男生和女生进行深入调查，发现他们分别在一周内参加各项体育活动的时间不等，根据调查数据绘制了以下折线统计图：
一周内参加各项体育活动时间折线统计图
(1)、填空：m 的值为；(2)、根据上述统计图表填写下表中的相关统计量：年级
参加各项体育活动时间的中位数
参加各项体育活动时间的方差
男生
54.4
女生
11
(3)、请你对所在学校落实国家“双减政策”采取的措施，写出一条合理的评价或建议．23. 为落实“双减”和“五项管理”，促进每一个孩子全面发展、健康成长，各级各部门都做出了有力举措．某班同学分三组进行教学实践活动调查，三组同学分别对七年级40名同学作业管理情况，八年级30名同学读物管理情况，九年级30名同学睡眠管理情况进行全面调查，并分别用扇形图、频数分布直方图、表格来描述得到的数据．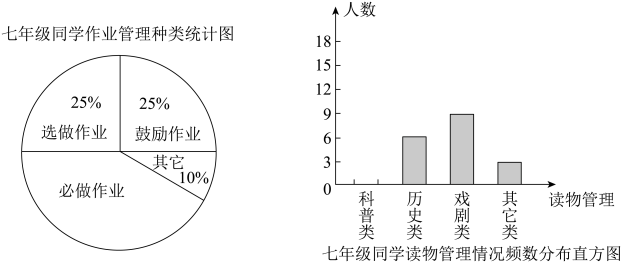
九年级同学睡眠管理时间情况统计表
时间
9小时左右
10小时左右
11小时左右
8小时左右
人数（人）
5
8
12
5
根据以上信息，请回答下列问题：
(1)、七年级40名同学中必做作业的人数是多少？(2)、补全八年级30名同学读物管理情况频数分布直方图：(3)、九年级30名同学睡眠时间的平均时间大约是多少小时？