浙江省衢州教学联盟体2022-2023学年八年级上学期数学期中教学诊断试题卷
试卷更新日期：2022-12-07 类型：期中考试
一、选择题（本题有10小题，每小题3分，共30分）
-
1. 出行安全，认识交通路标非常重要.下列是部分交通路标，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列各组长度的线段能构成三角形的是（ ）A、1cm，2cm，4cm B、3cm，4cm，7cm C、4cm，4cm，10cm D、3cm，4cm，5cm3. 若 ， 则下列式子中，不正确的是（ ）A、 B、 C、 D、4. 下列语句不是命题的是 （ ）A、x与y的和等于x+y吗？ B、不平行的两条直线只有一个交点 C、两点之间线段最短 D、相等的角是对顶角5. 已知的三条边之比为3：4：5，则这个三角形是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形6. 用尺规作图作∠APB的平分线PQ，痕迹如图所示，则此作图的依据是（ ）
A、(ASA) B、(SSS) C、(SAS) D、(AAS)7. 若等腰三角形的两条边长为2和5，则这个等腰三角形的周长为（ ）A、7或15 B、9或12 C、9 D、128. 如图，将一副三角板重叠放在一起，使直角顶点重合于点O.若∠AOC=140° ，则∠BOD的度数是（ ）
A、30° B、40° C、50° D、60°9. 如图，CD是等腰三角形 △ABC底边上的中线，BE平分∠ABC，交CD于点E，AC＝8，DE＝2，则 △ BCE的面积是（ ）
A、4 B、6 C、8 D、1210. 在如图的网格上，能找出几个格点，使每一个格点与A，B两点能构成的等腰三角形个数为（ ）
A、4个 B、5个 C、6个 D、7个二、填空题（本题有8小题，每小题3分，共24分）
-
11. 请用不等号（>或<）填空：－50.12. 命题“如果a＞0，那么a2＞0”的逆命题为.13. 如图，已知∠ABC=∠DBC，要使≌ ， 请添加一个条件 ． （只需写出一个条件）
14. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，如果∠A=40°，则∠1=度.
15. 如图，△ABC是直角三角形，所有的四边形都是正方形，其中最大的正方形的边长为9cm， 则正方形I，Ⅱ的面积之和为cm2 ．
16. 如图，有一张直角三角形纸片，两直角边AC＝4cm，BC＝8cm，将△ABC折叠，使点B与点A重合，折痕为DE，则CD的长是 ．
17. 如图，在 中， 垂直平分 ，点P为直线 上一动点，则 周长的最小值是 ．
18. 如图所示，△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P，若∠BPC＝40°，则∠CAP＝ ．
三、解答题（本题有6小题，共46分. ）
-
19. 在数轴上表示下列不等式：(1)、(2)、20. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形：
(1)、在图（1）中，画一个等腰三角形，使它的面积等于6；(2)、在图（2）中，画一个直角三角形，使它的三边长都是有理数；21. 如图，已知Rt△ABC与Rt△DEF中，∠A＝∠D＝90°，点B、F、C、E在同一直线上，且AB＝DE，BF＝CE，求证：∠B＝∠E．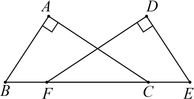
22. 如图，一个零件的形状如图所示，∠A=90°，工人师傅量的这个零件各边的尺寸如图所示．
(1)、求证：BC⊥BD(2)、求这个四边形的面积．23. 我们新定义一种三角形：如果一个三角形两条边的平方和等于第三边平方的4倍，那么这个三角形叫做常态三角形．例如：某三角形三边长分别是4，和8，因为 ， 所以这个三角形是常态三角形．
(1)、若△ABC三边长分别是5，6和8，请判断此三角形是否为常态三角形，并说明理由；(2)、如图，Rt△ABC中，∠ACB＝90°， BC＝ ， 点D为AB的中点，连接CD，若△ACD是常态三角形，求AC的长.24. 如图1，在△ABC中， BE平分∠ABC交AC边于点E，过点E作DE∥BC交AB于点D，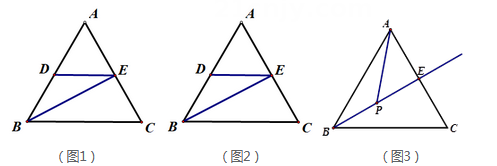
(1)、求证：BD=DE；(2)、若点D为AB中点(图2)，AB=6，求线段BC的长；(3)、在（2）条件下，若∠BAC=60°，动点P从点B出发，以每秒1个单位的速度沿射线BE运动(图3)，请直接写出当△ABP为等腰三角形时t的值.