四川省乐山市市中区2022-2023学年九年级上学期期中调研考试数学试题

试卷更新日期：2022-12-07 类型：期中考试

进入出卷网下载

一、选择题：本大题共10题，每题3分，共30分.

1. 使二次根式 $\sqrt{x - 1}$ 有意义的 $x$ 的取值范围是（）

A、 $x \neq 1$ B、 $x > 1$ C、 $x \leq 1$ D、 $x \geq 1$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 \sqrt{2} - \sqrt{2} = 2$ C、 $\sqrt{12} = 2 \sqrt{3}$ D、 $\sqrt{6} \div \sqrt{2} = 3$

查看试题解析
3. 一元二次方程x²﹣2x=0的根是（　　）

A、x=2 B、x=0 C、x₁=0，x₂=2 D、x₁=0，x₂=﹣2

查看试题解析
4.
如图所示的三个矩形中，其中相似形是（　　）

A、甲与乙 B、乙与丙 C、甲与丙 D、以上都不对

查看试题解析
5. 若数x、y满足 $\sqrt{x - 2} + {(y - 3)}^{2} = 0$ ，则 $\sqrt{2 x + 3 y + 3}$ 等于（）

A、0 B、5 C、4 D、 $\pm$ 4

查看试题解析
6. 如果关于 $x$ 的一元二次方程 $a x^{2} + x - 1 = 0$ 有两个实数根，则 $a$ 的取值范围是（）

A、 $a$ ＞ $- \frac{1}{4}$ B、 $a$ $\geq$ $- \frac{1}{4}$ C、 $a$ $\geq$ $- \frac{1}{4}$ 且 $a \neq 0$ D、 $a$ ＞ $- \frac{1}{4}$ 且 $a \neq 0$

查看试题解析
7. 如图，在平行四边形ABCD中，点E在AD上，连接CE并延长交 BA延长线于点F，若AE：AD=2：3，CD=3cm，则AF的长为（）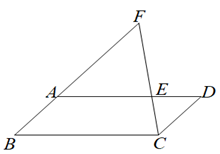

A、5cm B、6cm C、7cm D、8cm

查看试题解析
8. 某超市1月份的营业额是400万元，第一季度的营业额共2000万元，如果每月的增长率都是x，根据题意列出的方程应该是（）

A、400(1＋x)²=2000 B、400(1＋2x)=2000 C、400＋400(1＋x)＋400(1＋x)²=2000 D、400(1＋3x)=2000

查看试题解析
9. 如图，在Rt△ABC中，∠C=90°，放置边长分别为3，4，x的三个正方形，则x的值为（）

A、12 B、7 C、6 D、5

查看试题解析
10. 如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连结OE，∠ADC＝60°，AB＝ $\frac{1}{2}$ BC＝1.

有下列结论：①∠CAD＝30°；②BD＝ $\sqrt{7}$ ；③S_{平行四边形ABCD}＝AB·AC；④OE＝ $\frac{1}{4}$ AD；⑤S_△APO＝ $\frac{\sqrt{3}}{12}$ .其中正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题：本大题共6个小题，每小题3分，共18分．

11. 已知 $\frac{x}{y} = \frac{4}{3}$ ，则 $\frac{x - y}{y}$ = ．

查看试题解析
12. 已知 $x_{1}$ 、 $x_{2}$ 是方程 $2 x^{2} - 5 x - 3 = 0$ 的两个根，则 $x_{1} x_{2} =$ .

查看试题解析
13. 如图，点D、E分别是AB、AC的中点，则S_△_ADE∶S_四边形_BCED＝.

查看试题解析
14. 若三角形的三边长为2、x、5，化简 $\sqrt{{(3 - x)}^{2}} - \sqrt{{(x - 7)}^{2}}$ ＝.

查看试题解析
15. 利用图形的分、和、移、补探索图形关系，是我国传统数学的一种重要方法．如图1，BD是矩形ABCD的对角线，将△BCD分割成两对全等的直角三角形和一个正方形，然后按图2重新摆放，观察两图，若a＝4，b＝2，则矩形ABCD的面积是．

查看试题解析
16. 如图，在矩形ABCD和矩形AEGH中，AD∶AB=AH∶AE=1∶2.则DH∶CG∶BE= .

查看试题解析

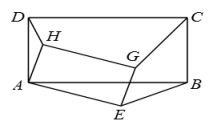
三、（本大题共3题.每题9分，共27分）

17. 计算： $\sqrt{25} + | 1 - \sqrt{3} | + \sqrt{27}$ .

查看试题解析
18. 解方程： $x^{2} - 2 x - 3 = 0$ .

查看试题解析
19. 如图，在△ABC中，DE∥BC，DF∥AC.求证：△ADE∽△DBF．

查看试题解析

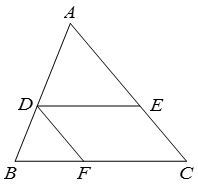
四、（本大题共3题.每题10分，共30分）

20. 先化简，再求值： $(1 - \frac{4}{x + 3}) \div \frac{x^{2} - 2 x + 1}{2 x + 6}$ ，其中 $x = \sqrt{2} + 1$ ．

查看试题解析
21. 已知实数 $a$ 、 $b$ 满足 $b = \sqrt{a - 2} + \sqrt{2 - a} - 3$ ，求 $a^{b}$ 的值．

查看试题解析
22. 材料：为解方程 $x^{4} - x^{2} - 6 = 0$ ，可将方程变形为 ${(x^{2})}^{2} - x^{2} - 6 = 0$ ，然后设 $x^{2} = y$ ，则 ${(x^{2})}^{2} = y^{2}$ ，原方程化为 $y^{2} - y - 6 = 0$ ，
解得 $y_{1} = - 2$ ， $y_{2} = 3$ ．

当 $y_{1} = - 2$ 时， $x^{2} = - 2$ 无意义，舍去；当 $y_{2} = 3$ 时， $x^{2} = 3$ ，解得 $x = \pm \sqrt{3}$ ．

∴原方程的解为 $x_{1} = - \sqrt{3}$ ， $x_{2} = + \sqrt{3}$ ．

问题：利用上述材料的解题方法，解方程 ${(x^{2} - x)}^{2} - 4 (x^{2} - x) - 12 = 0$ ．

查看试题解析

五、（本大题共2题.每题10分，共20分）

23. 某超市销售一种矿泉水，进价为每箱24元，现在的售价为每箱36元，每月可销售60箱．经市场调查发现：若这种矿泉水的售价每降价1元，则每月的销量将增加10箱．如果该超市想要每月销售这种矿泉水的利润为650元，那么每箱矿泉水需要降价多少元？

查看试题解析
24. 关于 $x$ 的一元二次方程 $x^{2} - (2 m - 1) x + m^{2} - m = 0$ .

(1)、证明：不论 $m$ 为何值，方程总有两个不相等的实数根.

(2)、设 $x_{1}$ 、 $x_{2}$ 是方程 $x^{2} - (2 m - 1) x + m^{2} - m = 0$ 的两个实根，是否存在 $m$ 值，使得 $2 x_{1} + 2 x_{2} = 3 x_{1} \cdot x_{2}$ ，请说明理由.

(3)、在Rt△ABC中，斜边AB=5， BC、AC的长恰是方程 $x^{2} - (2 m - 1) x + m^{2} - m = 0$ 的两个根，求Rt△ABC的面积.

查看试题解析

六、（本大题共2题.25题12分，26题13分，共25分）

25. 如图，在Rt△ACB中，∠C＝90°， $A C = 4 cm$ ， $B C = 3 cm$ ，点 $P$ 由 $B$ 出发沿 $B A$ 方向向点 $A$ 匀速运动速度为 $1cm/s$ ；点 $Q$ 由 $A$ 出发沿 $A C$ 方向向点 $C$ 匀速运动，速度为 $2cm/s$ ；连接 $P Q$ ．若设运动的时间为 $t (s) (0< t <2)$ ，解答下列问题：

(1)、当 $t$ 为何值时，点 $A$ 在 $P Q$ 垂直平分线上？

(2)、当 $t$ 为何值时，△APQ为直角三角形？

(3)、是否存在某一时刻 $t$ ，使线段 $P Q$ 恰好把Rt△ACB的面积平分？若存在，求出此时 $t$ 的值；若不存在，说明理由．

查看试题解析
26. 如图，在△ABC中，AB＝AC＝6cm，BC＝8cm，点E是线段BC边上的一动点（不含B、C两端点），连结AE，作∠AED＝∠B，交线段AB于点D．

(1)、求证： $△ B D E ∽ △ C E A$ ；

(2)、设BE＝x，AD＝y，请写出y与x之间的函数关系式，并求出y的最小值；

(3)、点E在运动的过程中， $△ A D E$ 能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由．

查看试题解析