四川省乐山市市中区2022-2023学年八年级上学期期中测试数学试题

试卷更新日期：2022-12-07 类型：期中考试

进入出卷网下载

一、选择题：本大题共10题，每题3分，共30分.

1. 在四个实数-2， $0$ ， $- \sqrt{3}$ ， -1中，最小的实数是（）

A、-2 B、0 C、 $- \sqrt{3}$ D、-1

查看试题解析
2. 下列说法中正确的是（）

A、-4的平方根为 $\pm 2$ B、-4的算术平方根为-2 C、0的平方根与算术平方根都是0 D、 ${(- 4)}^{2}$ 的平方根为-4

查看试题解析
3. 下列句子是命题的是（）

A、画 $∠ A O B = 30 °$ B、小于直角的角是锐角吗？ C、连结CD D、若 $a + b = c + b$ ，则 $a = c$

查看试题解析
4. 下列能用平方差公式计算的是（）

A、 $(- x + y) (x + y)$ B、 $(- x + y) (x - y)$ C、 $(x + 2) (2 + x)$ D、 $（ 2 x + 3) (3 x - 2)$

查看试题解析
5. 若 $x^{2} + 2 k x + 64$ 是完全平方式，则k的值为（）

A、8 B、±8 C、16 D、±16

查看试题解析
6. 已知△ABC≌△DEF，且∠A与∠D是对应角，∠B和∠E是对应角，则下列说法中正确的是（）

A、AC与DF是对应边 B、AC与DE是对应边 C、AC与EF是对应边 D、不能确定AC的对应边

查看试题解析
7. 若 $(x - 1) (x^{2} + a x + 2)$ 的展开式中不含 $x^{2}$ ，则 $a$ 的值（）

A、-2 B、-1 C、0 D、1

查看试题解析
8. 如果 $(x + 5) (2 x - n) = 2 x^{2} + m x - 15$ ，则（）

A、 $m = 7 ， n = 3$ B、 $m = 7 ， n = - 3$ C、 $m = - 7 ， n = - 3$ D、 $m = - 7 ， n = 3$

查看试题解析
9. 已知a，b为不同的两个实数，且满足 $a b > 0$ ， $a^{2} + b^{2} = 9 - 2 a b$ ，当 $a - b$ 为整数时，ab的值为（）

A、 $\frac{5}{4}$ 或2 B、 $\frac{9}{4}$ 或 $\frac{5}{4}$ C、 $\frac{1}{4}$ 或2 D、 $\frac{9}{4}$ 或2

查看试题解析
10. 如图所示，∠E=∠F=90°，AE=AF，AB=AC.
有下列结论：
①∠FAN=∠EAM；②EM=FN；③CD=DN；④△ACN≌△ABM．
其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：本大题共6个小题，每小题3分，共18分．

11. 25的平方根：.

查看试题解析
12. $(a b^{2} - 2 a^{2} b + a b) \div a b =$ .

查看试题解析
13. 规定：在实数范围内定义一种运算☆，其规则是 $a ☆ b = a^{2} - b^{2}$ ，若 $(x - 2) ☆ 3 = 0$ ，则 $x$ 的值为.

查看试题解析
14. 若 $（ 2 a^{2} + 2 b^{2} + 1) (2 a^{2} + 2 b^{2} - 1) = 15$ ，则 $a^{2} + b^{2} =$ .

查看试题解析
15. 如图，已知四边形ABCD中，AB＝12厘米，BC＝8厘米，CD＝14厘米，∠B＝∠C，点E为线段AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为厘米/秒时，能够使△BPE与以C、P、Q三点所构成的三角形全等.

查看试题解析
16. 南宋数学家杨辉在其著作《详解九章算法》中揭示了 ${(a + b)}^{n}$ （n为非负整数）展开式的项数及各项系数的有关规律，后人也将右表称为“杨辉三角”．
则① ${(a + b)}^{20}$ 中，第三项系数为；

② ${(a - b)}^{6}$ 展开式为.

查看试题解析

三、计算题（本题共4小题，17、18小题各8分，19、20小题各10分，共36分）

17.

(1)、 ${(2 x - 1)}^{2} + (- 2 x + 1) (1 + 2 x)$ ；

(2)、 ${(- 3 x^{2} y)}^{2} \cdot \frac{2}{3} x y z \div \frac{3}{4} x^{2} z$ .

查看试题解析
18. 运用公式进行简便计算.

(1)、 ${10.2}^{2} - 10.2 \times 2.4 + 1.44$ ；

(2)、 $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ... (1 - \frac{1}{2022^{2}})$ .

查看试题解析
19. 已知 $x + y = 4$ ， $x^{2} + y^{2} = 10$ ，求下列各式的值：

(1)、 $x y$ ；

(2)、 $x - y$ .

查看试题解析
20. 将下列各式分解因式；

(1)、 $25 {(x - y)}^{3} + y^{2} {(y - x)}^{3}$ ；

(2)、 ${(m^{2} + n^{2})}^{2} - 4 m^{2} n^{2}$

查看试题解析

四、（本题共4小题，21~23每小题10分，24小题11分，共41分）

21. 化简求值：

(1)、 $(3 x^{4} - 2 x^{3}) \div (- x) - (x - x^{2}) \cdot 3 x ，$ 其中 $x = - \frac{1}{3}$ ；

(2)、 ${(a - 3 b)}^{2} + {(3 a + b)}^{2} - {(a + 5 b)}^{2} + {(a - 5 b)}^{2} ，$ 其中 $a = - 6 ， b = - 4$ .

查看试题解析
22. 如图，E，F分别是等边三角形ABC的边AB，AC上的点，且BE=AF，CE，BF交于点P．

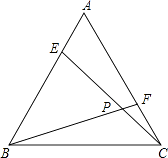(1)、求证：CE=BF；

(2)、求∠BPC的度数．

查看试题解析
23. 甲乙两人共同计算一道整式乘法题 $(2 x + a) (3 x + b)$ .甲由于把第一个多项式中的“ $+ a$ ”看成了“ $- a$ ”，得到的结果为 $6 x^{2} + 11 x - 10$ .乙由于漏抄了第二个多项式中 $x$ 的系数，得到的结果为 $2 x^{2} - 9 x + 10$ .

(1)、求正确的 $a$ 、 $b$ 的值；

(2)、计算出这道整式乘法题的正确结果.

查看试题解析
24. 已知，若实数a、b、c满足等式 $5^{a} = 4$ ， $5^{b} = 6$ ， $5^{c} = 9$ .

(1)、求 $5^{2 a + b}$ 的值；

(2)、求 $5^{b - 2 c}$ 的值；

(3)、求出 $a$ 、 $b$ 、 $c$ 之间的数量关系.

查看试题解析

五、简答题（本题共2小题，25小题12分，26小题13分，共25分）

25. 如图，CD经过∠BCA顶点C的一条直线，CA=CB．E，F分别是直线CD上两点，且∠BEC=∠CFA=∠α．

(1)、若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：
①如图1，若∠BCA=90°，∠α=90°，则BECF；EF|BE-AF|；（填“＞”，“＜”或“=”）

②如图2，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件，使①中的两个结论仍然成立，并证明两个结论成立；

(2)、如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）．

查看试题解析
26. 教科书中这样写道：“我们把多项式 $a^{2} + 2 a b + b^{2}$ 及 $a^{2} - 2 a b + b^{2}$ 叫做完全平方式”，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法。配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等.
例如：分解因式：x²＋2x－3.

原式. $= x^{2} + 2 x - 3 = (x^{2} + 2 x + 1) - 4 = (x + 1 + 2) (x + 1 - 2) = (x + 3) (x - 1)$

例如：求代数式 $2 x^{2} + 4 x - 6$ 的最小值.

原式=2x²+4x-6=2(x+1)²-8

∴当 $x = - 1$ 时， $2 x^{2} + 4 x - 6$ 有最小值，最小值是－8.

(1)、请用上述方法分解因式： $a^{2} - 2 a - 3 =$ ；

(2)、试说明：x、y取任何实数时，多项式 $x^{2} + y^{2} - 4 x + 2 y + 6$ 的值总为正数；

(3)、当m、n为何值时，多项式有最小值，并求出 $m^{2} - 2 m n + 2 n^{2} - 4 m - 4 n + 25$ 这个最小值.

查看试题解析