北师大版数学八年级上册《 第四章 一次函数》期末高分突破卷
试卷更新日期:2022-12-07 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 下列所述不属于函数关系的是( )A、长方形的面积一定,它的长和宽的关系 B、x+2与x的关系 C、匀速运动的火车,时间与路程的关系 D、某人的身高和体重的关系2. 下列图象中,表示y是x的函数的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一次函数与y轴的交点是( )A、(0,2) B、(0,) C、(2,0) D、( , 0)4. 函数中自变量x的取值范围是( )A、 B、 C、 D、5. 下列四组点中,在同一个正比例函数图象上的一组点是( )A、 , B、 , C、 , D、 ,6. 一次函数的图像经过点 , 每当x增加1个单位时,y增加3个单位,则此函数图象向上平移2个单位长度的表达式是( )A、 B、 C、 D、7. 已知点都在直线上,则的大小关系是( )A、 B、 C、 D、8. 已知一次函数y=kx+b,函数值y随自变量x的增大而减小,且kb>0,则函数y=kx+b的图象大致是( )A、
3. 一次函数与y轴的交点是( )A、(0,2) B、(0,) C、(2,0) D、( , 0)4. 函数中自变量x的取值范围是( )A、 B、 C、 D、5. 下列四组点中,在同一个正比例函数图象上的一组点是( )A、 , B、 , C、 , D、 ,6. 一次函数的图像经过点 , 每当x增加1个单位时,y增加3个单位,则此函数图象向上平移2个单位长度的表达式是( )A、 B、 C、 D、7. 已知点都在直线上,则的大小关系是( )A、 B、 C、 D、8. 已知一次函数y=kx+b,函数值y随自变量x的增大而减小,且kb>0,则函数y=kx+b的图象大致是( )A、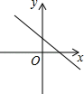 B、
B、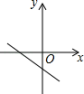 C、
C、 D、
D、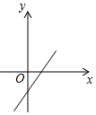 9. 正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=-x-k的图象是( )A、
9. 正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=-x-k的图象是( )A、 B、
B、 C、
C、 D、
D、 10. 根据图中的程序,当输入x =3时,输出的结果y =( )
10. 根据图中的程序,当输入x =3时,输出的结果y =( )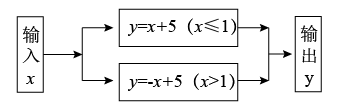 A、2 B、8 C、8或2 D、16
A、2 B、8 C、8或2 D、16二、填空题(每题3分,共15分)
-
11. 点 , 在一次函数的图象上,则 . (填“>”,“<”或“=”)12. 如图,直线()过点 , 则关于的方程的解为;
 13. 已知点P在直线上,且点P到y轴的距离为1,则点P的坐标为 .14. 已知 y是关于x的一次函数,下表列出了部分对应值,则a的值为 .
13. 已知点P在直线上,且点P到y轴的距离为1,则点P的坐标为 .14. 已知 y是关于x的一次函数,下表列出了部分对应值,则a的值为 .x 1 2 3 y 3 a 5 15. 如图放置的△OAB1 , △B1A1B2 , OB2A2B3都是边长为2的等边三角形,边0A在y轴上,点B1 , B2 , B3 , ……都在直线y=x上,则点A2022的坐标是
三、解答题(共7题,共75分)
-
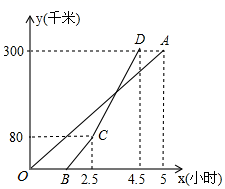
16. 已知: , 与 成正比例, 与x成反比例.当 时, ;当 时, .求y与x的函数解析式.17. 甲,乙两地相距300千米.一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,线段CD对应的函数解析式是y=110x﹣195(2.5≤x≤4.5),在轿车行进过程中,轿车行驶多少时间,两车相距15千米?
 18. 如图,在平面直角坐标系中,直线 与直线 相交于点 .
18. 如图,在平面直角坐标系中,直线 与直线 相交于点 . (1)、求m,b的值;(2)、求 的面积;(3)、点P是x轴上的一点,过P作垂于x轴的直线与 的交点分别为C,D,若P点的横坐标为n,当 时直接写出n的取值范围.19. 如图,在平面直角坐标系中,过点B(4,0)的直线AB与直线AD相交于点A(3,2),且点D(0,-1),动点M在直线AD上运动.
(1)、求m,b的值;(2)、求 的面积;(3)、点P是x轴上的一点,过P作垂于x轴的直线与 的交点分别为C,D,若P点的横坐标为n,当 时直接写出n的取值范围.19. 如图,在平面直角坐标系中,过点B(4,0)的直线AB与直线AD相交于点A(3,2),且点D(0,-1),动点M在直线AD上运动. (1)、求直线AB的解析式.(2)、求△ACD的面积.(3)、当△MCD的面积是△ACD的面积的 时,求此时点M的坐标.20. 年新冠肺炎疫情在全球蔓延,全球疫情大考面前,中国始终同各国安危与共、风雨同舟,时至 月,中国已经向 多个国家和国际组织提供医疗物资援助.某次援助,我国组织 架飞机装运口罩、消毒剂、防护服三种医疗物资共 吨,按计划 架飞机都要装运,每架飞机只能装运同一种医疗物资,且必须装满.根据如下表提供的信息,解答以下问题:
(1)、求直线AB的解析式.(2)、求△ACD的面积.(3)、当△MCD的面积是△ACD的面积的 时,求此时点M的坐标.20. 年新冠肺炎疫情在全球蔓延,全球疫情大考面前,中国始终同各国安危与共、风雨同舟,时至 月,中国已经向 多个国家和国际组织提供医疗物资援助.某次援助,我国组织 架飞机装运口罩、消毒剂、防护服三种医疗物资共 吨,按计划 架飞机都要装运,每架飞机只能装运同一种医疗物资,且必须装满.根据如下表提供的信息,解答以下问题:防疫物资种类
口罩
消毒剂
防护服
每架飞机运载量(吨)
每吨物资运费(完)
(1)、若有 架飞机装运口罩,有 架飞机装运消毒剂,求 与 之间的函数关系式;(2)、若此次物资运费为 元,求 与 之间的函数关系式;(3)、如果装运每种医疗物资的飞机都不少于 架,那么怎样安排运送物资,方能使此次物资运费最少,最少运费为多少元?21. 如图表示甲、乙两车沿相同路线从A地出发到B地行驶过程中,路程y(千米)随时间x(时)变化的图象.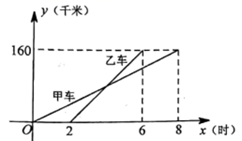 (1)、乙车比甲车晚出发小时,甲车的速度是千米/时;(2)、当 时,求乙车行驶路程随时间变化的函数表达式;(3)、从乙车出发到停止期间,乙车出发多长时间,两车相距20千米?22. 在平面直角坐标系中,对于 、 两点,用以下方式定义两点间的“极大距离” ;若 ,则 ;若 ,则 .例如:如图,点 ,则 .
(1)、乙车比甲车晚出发小时,甲车的速度是千米/时;(2)、当 时,求乙车行驶路程随时间变化的函数表达式;(3)、从乙车出发到停止期间,乙车出发多长时间,两车相距20千米?22. 在平面直角坐标系中,对于 、 两点,用以下方式定义两点间的“极大距离” ;若 ,则 ;若 ,则 .例如:如图,点 ,则 . (1)、(理解定义)
(1)、(理解定义)
若点 、 ,则 .(2)、在点 、 、 、 中,到坐标原点O的“极大距离”是2的点是.(填写所有正确的字母代号)(3)、(深入探索)
已知点 , ,O为坐标原点,求a的值.(4)、(拓展延伸)
经过点 的一次函数 (k、b是常数, )的图象上是否存在点P,使 ,O为坐标原点,直接写出点P的个数及对应的k的取值范围.