2022-2023学年苏科版数学七上尖子生考点培优专题训练6 有关行程的动点问题

试卷更新日期：2022-12-07 类型：复习试卷

进入出卷网下载

一、单选题

1. 甲、乙两人在环形跑道上匀速跑步，他们同时从同一地点出发，当两人往相反方向跑步时，每隔48秒相遇一次；当两人往相同方向跑步时，每隔8分钟相遇一次。已知甲比乙每分钟快60米。则甲的速度为（）米/秒。

A、4 B、4.5 C、5 D、5.5

查看试题解析
2. 甲、乙两运动员在长为100m的直道AB（A，B为直道两端点）上进行匀速往返跑训练，两人同时从A点起跑，到达B点后，立即转身跑向A点，到达A点后，又立即转身跑向B点...若甲跑步的速度为5m/s，乙跑步的速度为4m/s，则起跑后2分钟内，两人相遇的次数为（）

A、7 B、6 C、5 D、4

查看试题解析
3. 如图，数轴上的点O和点A分别表示0和10，点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次，B是线段OA的中点，设点P运动时间为t秒（t不超过10秒）.若点P在运动过程中，当PB＝2时，则运动时间t的值为（）

A、 $\frac{3}{2}$ 秒或 $\frac{5}{2}$ 秒 B、 $\frac{3}{2}$ 秒或 $\frac{7}{2}$ 秒或 $\frac{13}{2}$ 秒或 $\frac{15}{2}$ 秒 C、3秒或7秒或 $\frac{13}{2}$ 秒或 $\frac{17}{2}$ 秒 D、 $\frac{3}{2}$ 秒或 $\frac{7}{2}$ 秒或 $\frac{13}{2}$ 秒或 $\frac{17}{2}$ 秒

查看试题解析
4. 如图所示，甲､乙两人沿着边长为70米的正方形，按 $A \to B \to C \to D \to A \to \cdot \cdot \cdot$ 的方向行走．甲从A点以65米/分的速度行走，乙从B点以72米/分的速度行走，甲､乙两人同时出发，当乙第一次追上甲时，所在正方形的边为（）

A、 $A B$ B、 $B C$ C、 $C D$ D、 $A D$

查看试题解析
5. 随着科技的进步，我们可以通过手机APP实时查看公交车到站情况.小明想乘公交车，可又不想静静地等在A站.他从A站往B站走了一段路，拿出手机查看了公交车到站情况，发现他与公交车的距离为720m（如图），此时有两种选择：（1）与公交车相向而行，到A公交站去乘车；（2）与公交车同向而行，到B公交站去乘车.假设小明的速度是公交车速度的 $\frac{1}{5}$ ，若要保证小明不会错过这辆公交车，则A，B两公交站之间的距离最大为（）

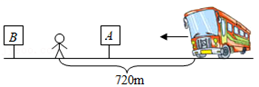A、240m B、300m C、320m D、360m

查看试题解析

二、填空题

6. 一列火车匀速行驶，经过一条长600米的隧道需要45秒的时间，隧道的顶部一盏固定灯，在火车上垂直照射的时间为15秒，则火车的长为.

查看试题解析
7. 如图，在数轴上A点表示数﹣2，B点表示数6，若在原点O处放一挡板，一小球甲从点A处以1个单位/秒的速度向左运动；同时另一小球乙从点B处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，则经过秒，甲、乙两小球到原点的距离相等.

查看试题解析
8. 已知点O是数轴的原点，点A、B、C在数轴上对应的数分别是﹣12、b、c ，且b、c满足（b﹣9）²+|c﹣15|＝0，动点P从点A出发以2单位/秒的速度向右运动，同时点Q从点C出发，以1个单位/秒速度向左运动，O、B两点之间为“变速区”，规则为从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速，从点B运动到点O期间速度变为原来的3倍，之后立刻恢复原速，运动时间为秒时，P、Q两点到点B的距离相等．

查看试题解析
9. 如图，已知等边三角形 $A B C$ 的边长为24厘米，甲、乙两动点同时从顶点 $A$ 出发，甲以1厘米/秒的速度沿等边三角形的边按顺时针方向移动，乙以3厘米/秒的速度沿等边三角形的边按逆时针方向移动，相遇后甲、乙的速度均增加1厘米/秒且都改变原方向移动．则第二次相遇时乙与最近顶点的距离是厘米．

查看试题解析
10. 如图所示，数轴上有A，B，C，三个点，点A表示的数是-2，点B表示的数是22，点C表示的数是43。现有两只电蚂蚁，蚂蚁P从点A出发以每秒5个单位长度的速度沿数轴的正方向运动，另一只电蚂蚁Q从点B出发，以每秒1个单位长度的速度，沿数轴的正方向运动。现两只电蚂蚁同时出发，在A、C两点之间来回运动（从点A向点C运动，到达点C后，立即原速返回，再次到达.A点后，立即调头，向点C运动）。当两只电蚂蚁P、Q 第10次迎面而遇（不包括追上相遇）时，相遇点所表示的数为．

查看试题解析

三、综合题

11. 一辆卡车从甲地匀速开往乙地，出发2小时后，一辆轿车从甲地去追这辆卡车，轿车的速度比卡车的速度每小时快30千米，但轿车行驶一小时后突遇故障修理15分钟后，又上路追这辆卡车，但速度减小了 $\frac{1}{3}$ ，结果又用两小时才追上这辆卡车，求卡车的速度．

查看试题解析
12. 如图，已知：数轴上点A表示的为8，B是数轴上一点，点B在点A左边且点A与点B的距离AB＝14，动点P、Q分别从点A、B两点同时向左移动，点P的速度为每秒3个单位长度，点Q的速度为每秒1个单位长度．

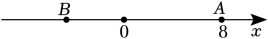(1)、写出数轴上点B表示的数；

(2)、经过多少秒以后，P、Q两点的距离为6个单位长度，并求出此时点P表示的数是多少？

(3)、若点P遇到点Q时立即掉头返回，速度不变，请问相遇后再过秒，点Q到原点的距离是点P到原点的距离的3倍．（直接写出答案即可）

查看试题解析
13. 数轴上 $A$ 点对应的数为-5， $B$ 点在 $A$ 点右边，电子蚂蚁甲、乙在 $B$ 分别以2个单位 $/$ 秒、1个单位 $/$ 秒的速度向左运动，电子蚂蚁丙在 $A$ 以3个单位 $/$ 秒的速度向右运动.

(1)、若电子蚂蚁丙经过 $5$ 秒运动到 $C$ 点，求 $C$ 点表示的数；

(2)、若丙与甲同时出发，经过4秒后丙与甲相距5个单位长度，求 $B$ 点表示的数；

(3)、若B点表示的数是15，设它们同时出发的时间为 $t$ 秒，是否存在 $t$ 的值，使丙到乙的距离是丙到甲的距离的2倍？若存在，求出 $t$ 值；若不存在，说明理由.

查看试题解析
14. 如图所示，已知数轴上A，B两点对应的数分别为－2，4，点P为数轴上一动点，其对应的数为x.

(1)、若点P到点A，B的距离相等，求点P对应的数x的值．

(2)、数轴上是否存在点P，使点P到点A，B的距离之和为8？若存在，请求出x的值；若不存在，说明理由．

(3)、点A，B分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P以5个单位长度/分的速度从O点向左运动．当遇到A时，点P立即以同样的速度向右运动，并不停地往返于点A与点B之间．当点A与点B重合时，点P经过的总路程是多少？

查看试题解析
15. 观察下列每对数在数轴上的对应点间的距离：3与5，4与 $- 2$ ， $- 1$ 与 $- 5$ ．并结合数轴与绝对值的知识，利用数形结合思想回答下列各题：

(1)、探究归纳：数轴上表示3和5的两点之间的距离是；数轴上表示4和 $- 2$ 的两点之间的距离是；数轴上表示数 $m$ 和 $n$ 的两点之间的距离是．

(2)、知识应用：若数轴上的点 $A$ 表示的数为 $x$ ，点 $B$ 表示的数为 $- 3$ ．并且 $A$ 、 $B$ 两点之间的距离为3，求 $x$ 的值．

(3)、拓展提高：已知， $C$ 、 $D$ 分别为数轴上的两点， $C$ 点对应的数为 $- 10$ ， $D$ 点对应的数为90．点 $D$ 以3个单位/秒的速度向左运动，同时点 $C$ 以2个单位/秒的速度向右运动，经过多长的时间 $C$ 、 $D$ 两点在数轴上相距40个单位长度．

查看试题解析
16. 如图，已知数轴上A，O，B三点对应的数分别为 $- 1$ ， 0，5，点P为数轴上任意一点，其对应的数为a．

(1)、如果点P到点A，B的距离相等，那么a的值为；

(2)、数轴上是否存在点P，使点P到点A的距离是点P到点B距离的2倍？若存在，请求出a的值；若不存在，请说明理由；

(3)、若点P从点O出发以每秒3个单位长度的速度运动，同时点A，B分别以每秒1个单位长度和2个单位长度的速度向右运动，运动时间为t秒．
①若点P向右运动，当点P到点A的距离是点P到点B距离2倍时，求t的值；
②若点P先向右运动遇到点B时立即向左运动，当点P与点A重合时，求t的值．

查看试题解析
17. 阅读理解：若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们称点C是[A，B]的好点．

例如，如图1，点A表示的数为-1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是[A，B]的好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D不是[A，B]的好点，但点D是[B，A]的好点．

知识运用：

(1)、若M、N为数轴上两点，点M所表示的数为-5，点N所表示的数为7．
①在数-5和7之间，数所表示的点是[M，N]的好点；

②在数轴上，数所表示的点是[N，M]的好点；

(2)、如图2，A、B为数轴上两点，点A所表示的数为-30，点B所表示的数为50．现有一只电子蚂蚁P从点B出发，以5个单位每秒的速度向左运动，到达点A停止，运动时间为t秒；同时另一只电子蚂蚁Q从A点的位置开始，以3个单位每秒的速度向右运动，并与P点同时停止．请求出P是[A，Q]的好点时的t的值．

(3)、在（2）的条件下，当t＝时，P、A和B中恰有一个点为其余两个点的好点．（直接写出结果）

查看试题解析
18. 已知数轴上两点A、B对应的数分别为 $- 1$ 、5．

(1)、请在数轴上标出点A和点B；

(2)、若P、Q两点分别从A、B两点同时出发，沿着数轴向右运动，其中点P的速度是每秒2个单位长度，点Q的速度是每秒1个单位长度，运动时间为t秒．
①若t秒后点P追上点Q，则t=秒；
②当点P追上点Q后，点P立即返回，当t=秒时，点P与点B之间的距离为两个单位长度；

(3)、若数轴上有一点M对应的数为 $- 5$ ，且点C从点M出发以每秒3个单位长度的速度沿着数轴向右运动，运动时间为t秒．若点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC，当 $A C + B C$ 取最小值时，求t的取值范围，并写出 $A C + B C$ 的最小值．

查看试题解析
19. 已知数轴上两点A、B对应的数分别为﹣1，3，点P为数轴上一动点，其对应的数为a．

(1)、若点P到点A、点B的距离相等，求点P对应的数．

(2)、数轴上是否存在一个点P，使点P到点A、点B的距离之和为8，若存在，求出a的值，若不存在，请说明理由．

(3)、若点A以每分钟2个单位长度向左运动，点B以每分钟6个单位长度向左运动；
①当点P以每分钟1个单位长度从数轴上的数2开始向左运动，A、B、P三点同时出发，几分钟后P点到点A、点B的距离相等？

②当点P以每分钟8个单位长度从原点开始向左运动，当遇到点A时；点P立即以同样的速度向右运动，当遇到点B时，点P立即以同样的速度向左运动，并不停地往返于点A与点B之间，A、B、P三点同时出发，求点A与点B重合时，点P所运动的总路程是多少个单位长度？

查看试题解析
20. 综合探究
【背景知识】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：如图①，若数轴上点A、点B表示的数分别为a，b（b＞a），则线段AB的长（点A到点B的距离）可表示为b－a．请用上面材料中的知识解答下面的问题：
【问题情境】如图②，一个点从数轴上的原点开始，先向左移动2个单位长度到达点A，再向右移动3个单位长度到达点B，然后再向右移动5个单位长度到达点C．

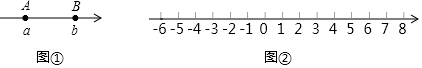(1)、【问题探究】请在图②中表示出A、B、C三点的位置；

(2)、【问题探究】若点P从点A出发，以每秒1个单位长度的速度沿数轴向左匀速运动，同时点M、N从点B、点C分别以每秒2个单位长度、每秒3个单位长度速度沿数轴向右匀速运动．设移动时间为t秒(t＞0)．
①A，B两点间的距离AB= ▲ ， AC= ▲ ；
②若点D、E分别是线段AB，BC的中点，求线段DE的长；
③用含t的代数式表示：t秒时，点P表示的数为 ▲ ，点M表示的数为 ▲ ，点N表示的数为 ▲ ；
④试探究在移动的过程中，3PN－4PM的值是否随着时间t的变化而变化？若变化说明理由；若不变，请求其值．

查看试题解析