北师大版数学八年级上册《第三章 位置与坐标》期末高分突破卷

试卷更新日期：2022-12-07 类型：复习试卷

进入 出卷网 下载

一、单选题（每题3分，共30分）

  • 1. 平面直角坐标系中，属于第四象限的点是（    ）
    A、(5 ， 3) B、(−5 ， 3) C、(5 ， −3) D、(−5 ， −3)

    查看试题解析

  • 2. 若点A(m ， −2) ， B(−4 ， n−3)关于x轴对称，则（   ）
    A、m=−4 ， n=5 B、m=−4 ， n=−5 C、m=4 ， n=1 D、m=4 ， n=−1

    查看试题解析

  • 3. 已知点A的坐标为(a+1 ， 3−a) ，  下列说法正确的是（    ）
    A、若点A在y轴上， 则a=3 B、若点A在一三象限角平分线上， 则a=1 C、若点A到x轴的距离是3 ， 则a=±6 D、若点A在第四象限， 则a的值可以为-2

    查看试题解析

  • 4. 2021年6月17日神舟十二号飞船于在甘肃酒泉发射升空，在太空驻留90天后于9月14日返回地球，下列描述能确定飞船着陆位置的是（    ）
    A、内蒙古中部 B、酒泉卫星发射中心东南方向1000km处 C、东经129°29'~97°10' D、北纬53°20'~37°20'

    查看试题解析

  • 5. 如图，小石同学在正方形网格中确定点A的坐标为（-1，1），点B的坐标为（2，0），则点C的坐标为（　　）

    A、（1，-2） B、（-2，1） C、（-1，-2） D、（1，-1）

    查看试题解析

  • 6. 若点P(2−m ， 5)在y轴上，则m的值等于（　　）
    A、2 B、7 C、−2 D、−3

    查看试题解析

  • 7. 国庆假期，小磊和小强去电影院观看了首部聚焦“外交官撤侨”的电影《万里归途》，若电影票上小磊的座号“5排6座”记作(5 ， 6) ， 则小强的座号“6排7座”可记作（        ）
    A、(−6 ， 7) B、(6 ， 7) C、(7 ， 6) D、(−6 ， −7)

    查看试题解析

  • 8. 在直角坐标系中，点M在第四象限，且到两坐标轴的距离都是4，则点M的坐标为（       ）
    A、(4 ， 4) B、(−4 ， 4) C、(−4 ， −4) D、(4 ， −4)

    查看试题解析

  • 9. 已知点A的坐标为(2 ， 3) ， 直线AB∥y轴，且AB=5 ， 则点B的坐标为（　　）
    A、(2 ， 8) B、(2 ， 8)或(2 ， −2) C、(7 ， 3) D、(7 ， 3)或(−3 ， 3)

    查看试题解析

  • 10. 如图，长方形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A(4，0)同时出发，沿长方形BCDE的边作环绕运动，物体甲按逆时针方向以2个单位/秒匀速运动，物体乙按顺时针方向以6个单位秒匀速运动，则两个物体运动后的第2021次相遇地点的坐标是（   ）

    A、(0，2) B、(﹣4，0) C、(0，﹣2) D、(4，0)

    查看试题解析

二、填空题（每题3分，共15分）

  • 11. 已知点M（m，n）与点N（-3，-5）关于×轴对称，则m+n=.

    查看试题解析

  • 12. 已知点M(2m−1 ， −3) ， 点N(5 ， 2) ， 直线MN∥y轴，则m的值为 ．

    查看试题解析

  • 13. 如图是一台雷达探测相关目标得到的结果，若记图中目标A的位置为(2，90°)，目标B 的位置为(4，30°)，现有一个目标C的位置为(3，m°)，且与目标B的距离为5，则目标C的位置为 ．

    查看试题解析

  • 14. 如图，OA平分∠BOD ， AC⊥OB于点C，且AC=3 ， 已知点A到y轴的距离是4，那么点A的坐标为.

    查看试题解析

  • 15. 如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（m，n），则经过第2021次变换后所得的A点坐标是 ．

    查看试题解析

三、解答题（共8题，共75分）

  • 16. 如图，方格纸中每个小正方形的边长均为1个单位长度，点A，B，C，D，O都在格点上．以点O为坐标原点，在图中建立适当的平面直角坐标系，并写出点A，B，C，D的坐标．

    查看试题解析

  • 17. △ABC在平面直角坐标系中的位置如图所示（每个小正方形的边长为1）．

    (1)、作出△ABC关于y轴对称的△A1B1C1；
    (2)、直接写出点C1的坐标；
    (3)、若P(a，a-1)是△ABC内部一点，点P关于y轴对称点为P'，且PP’=6，求点P'的坐标．

    查看试题解析

  • 18. 已知点P(3a−15 ， 2−a) ．
    (1)、若点P位于第四象限，它到x轴的距离是4 ， 试求出a的值：
    (2)、若点P位于第三象限且横、纵坐标都是整数， 试求点P的坐标．

    查看试题解析

  • 19.             
    (1)、若点(2a+3 ， a−3)在第一、三象限的角平分线上，求a的值；
    (2)、已知点P的坐标为(4−a ， 3a+6) ， 且点P到两坐标轴的距离相等，求点P的坐标．

    查看试题解析

  • 20. 如图，直线m是△ABC中BC边的垂直平分线，点P是直线m上的一动点，若AB=6 ， AC=4 ， BC=7 ．

    (1)、求PA+PB的最小值，并说明理由．
    (2)、求△APC周长的最小值．

    查看试题解析

  • 21. 如图，平面直角坐标系中，A（﹣2，1），B（﹣3，4），C（﹣1，3），过点（1，0）作x轴的垂线l．

    (1)、作出△ABC关于直线l的轴对称图形△A1B1C1；
    (2)、直接写出A1（ ， ），B1（ ， ），C1（ ， ）；
    (3)、在△ABC内有一点P（m，n），则点P关于直线l的对称点P1的坐标为（ ， ）（结果用含m，n的式子表示）．

    查看试题解析

  • 22. 如图是某地火车站及周围的简单平面图．（图中每个小正方形的边长代表1千米）

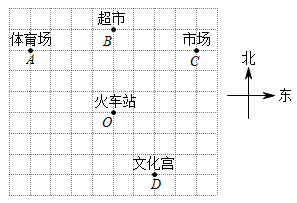    (1)、请以火车站所在的位置为坐标原点，以图中小正方形的边长为单位长度，建立平面直角坐标系，并写出体育场A、超市B、市场C、文化宫D的坐标；
    (2)、在（1）中所建的坐标平面内，若学校E的位置是（﹣3，﹣3），请在图中标出学校E的位置．

    查看试题解析

  • 23. 如图①，在矩形OACB中，点A在x轴正半轴上，点B在y轴正半轴上，点C在第一象限，OA=8，OB=6

    (1)、直接写出点C的坐标：；
    (2)、如图②，点G在BC边上，连接AG，将△ACG沿AG折叠，点C恰好与线段AB上一点C'重合，求线段CG的长度；

    (3)、如图③，P是直线y=2x－6上一点，PD⊥PB交线段AC于D．若P在第一象限，且PB=PD，试求符合条件的所有点P的坐标．

    查看试题解析