2022-2023学年苏科版数学七上尖子生考点培优专题训练5 与角有关的动点问题
试卷更新日期:2022-12-07 类型:复习试卷
一、单选题
-
1. 已知长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互余的角有( )
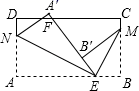 A、2个 B、3个 C、4个 D、5个2. 将一副三角板如图①的位置摆放,其中30°直角三角板的直角边与等腰直角三角板的斜边重合,30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合(为点O).现将30°的直角三角板绕点O顺时针旋转至如图②的位置,此时为25°,则( )
A、2个 B、3个 C、4个 D、5个2. 将一副三角板如图①的位置摆放,其中30°直角三角板的直角边与等腰直角三角板的斜边重合,30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合(为点O).现将30°的直角三角板绕点O顺时针旋转至如图②的位置,此时为25°,则( )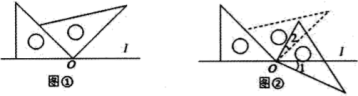 A、15° B、20° C、25° D、30°3. 如图,点O在直线 上,过O作射线 , ,一直角三角板的直角顶点与点O重合,边 与 重合,边 在直线 的下方.若三角板绕点O按每秒 的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线 恰好平分锐角 ,则t的值为( )
A、15° B、20° C、25° D、30°3. 如图,点O在直线 上,过O作射线 , ,一直角三角板的直角顶点与点O重合,边 与 重合,边 在直线 的下方.若三角板绕点O按每秒 的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线 恰好平分锐角 ,则t的值为( ) A、5 B、4 C、5或23 D、4或224. 如图. , 、分别是∠AOM和∠MOB的平分线,、分别是和的平分线,、分别是和的平分线,…,、分别是和的平分线,则的度数是( )
A、5 B、4 C、5或23 D、4或224. 如图. , 、分别是∠AOM和∠MOB的平分线,、分别是和的平分线,、分别是和的平分线,…,、分别是和的平分线,则的度数是( ) A、 B、 C、 D、5. 如图,按照上北下南,左西右东的规定画出方向十字线,∠AOE=m°,∠EOF=90°,OM、ON分别平分∠AOE和∠BOF,下面说法:
A、 B、 C、 D、5. 如图,按照上北下南,左西右东的规定画出方向十字线,∠AOE=m°,∠EOF=90°,OM、ON分别平分∠AOE和∠BOF,下面说法:①点E位于点O的北偏西m°;②图中互余的角有4对;③若∠BOF=4∠AOE,则∠DON=54°;④若 ,则n的倒数是 ,其中正确有( )
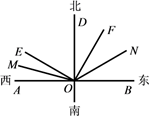 A、3个 B、2个 C、1个 D、0个
A、3个 B、2个 C、1个 D、0个二、填空题
-
6. 如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线AB的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 .
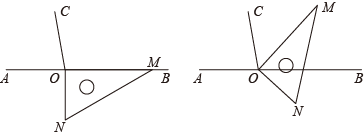 7. 如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,若ED′平分∠FEG , 且 在 内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为(用含n的代数式表示).
7. 如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,若ED′平分∠FEG , 且 在 内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为(用含n的代数式表示).
 8. 如图1, 为直线 上一点,作射线 ,使 ,将一个直角三角尺如图摆放,直角顶点在点 处,一条直角边 在射线 上.将图1中的三角尺绕点 以每秒10°的速度按逆时针方向旋转(如图2所示),在旋转一周的过程中,第 秒时, 所在直线恰好平分 ,则 的值为.
8. 如图1, 为直线 上一点,作射线 ,使 ,将一个直角三角尺如图摆放,直角顶点在点 处,一条直角边 在射线 上.将图1中的三角尺绕点 以每秒10°的速度按逆时针方向旋转(如图2所示),在旋转一周的过程中,第 秒时, 所在直线恰好平分 ,则 的值为.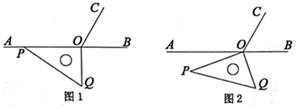 9. [知识背景]:三角形是数学中常见的基本图形,它的三个角之和为180°.等腰三角形是一种特殊的三角形,如果一个三角形有两边相等,那么这个三角形是等腰三角形,相等的两边所对的角也相等.
9. [知识背景]:三角形是数学中常见的基本图形,它的三个角之和为180°.等腰三角形是一种特殊的三角形,如果一个三角形有两边相等,那么这个三角形是等腰三角形,相等的两边所对的角也相等.
如图1,在三角形ABC中,如果AB=AC , 那么∠B=∠C . 同样,如果∠B=∠C , 则AB=AC , 即这个三角形也是等腰三角形.
[知识应用]:如图2,在三角形ABC中,∠ACB=90°,∠ABC=30°,将三角形ABC绕点C逆时针旋转α(0°<α<60°)度(即∠ECB=α度),得到对应的三角形DEC , CE交AB于点H , 连接BE , 若三角形BEH为等腰三角形,则α=°.
10. 小方同学设计了一个“魔法棒转不停”程序,如图所示,点 , 在直线 上,第一步, 绕点 顺时针旋转 度 至 ;第二步, 绕点 顺时针旋转 度至 ;第三步, 绕点 顺时针旋转 度至 , 以此类推,在旋转过程中若碰到直线 则立即绕点 反方向旋转.当 时,则 等于度.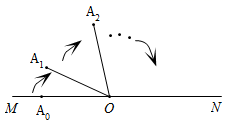
三、综合题
-
11. 如图1,点 、 、 共线且 , ,射线 , 分别平分 和 .
如图2,将射线 以每秒 的速度绕点 顺时针旋转一周,同时将 以每秒 的速度绕点 顺时针旋转,当射线 与射线 重合时, 停止运动.设射线 的运动时间为 .
 (1)、运动开始前,如图1, ,(2)、旋转过程中,当 为何值时,射线 平分 ?(3)、旋转过程中,是否存在某一时刻使得 ?若存在,请求出 的值;若不存在,请说明理由.12. 如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)、运动开始前,如图1, ,(2)、旋转过程中,当 为何值时,射线 平分 ?(3)、旋转过程中,是否存在某一时刻使得 ?若存在,请求出 的值;若不存在,请说明理由.12. 如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方. (1)、将图1中的三角板绕点O处逆时针旋转至图2,使一边OM在∠BOC的内部.且恰好平分∠BOC,求∠CON与∠AOM的度数.(2)、将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部.请探究:∠CON与∠AOM之间的数量关系,并说明理由.(3)、将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时.直线ON恰好平分锐角∠AOC,则t的值为秒(直接写出结果).13. 如图1,∠AOB是平角,∠COD是直角,射线OB在∠COD内部,OE,OF分别是∠BOD,∠AOC的平分线.
(1)、将图1中的三角板绕点O处逆时针旋转至图2,使一边OM在∠BOC的内部.且恰好平分∠BOC,求∠CON与∠AOM的度数.(2)、将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部.请探究:∠CON与∠AOM之间的数量关系,并说明理由.(3)、将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时.直线ON恰好平分锐角∠AOC,则t的值为秒(直接写出结果).13. 如图1,∠AOB是平角,∠COD是直角,射线OB在∠COD内部,OE,OF分别是∠BOD,∠AOC的平分线. (1)、如图1,若OB是∠COD的平分线,求∠AOF的度数;(2)、如图1,求∠EOF的度数;(3)、若改变∠COD的位置变化,如图2,当∠COD在直线AB的上方时,如图3,当射线OA在∠COD内部时,如图4,当∠COD在直线AB的下方时,∠EOF的度数发生变化吗?若不变,请直接写出∠EOF的度数;若不确定,请说明理由.14. 如图,∠AOB=90°,∠COD=60°.
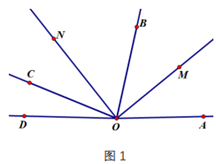
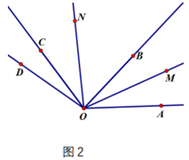
(1)、如图1,若OB是∠COD的平分线,求∠AOF的度数;(2)、如图1,求∠EOF的度数;(3)、若改变∠COD的位置变化,如图2,当∠COD在直线AB的上方时,如图3,当射线OA在∠COD内部时,如图4,当∠COD在直线AB的下方时,∠EOF的度数发生变化吗?若不变,请直接写出∠EOF的度数;若不确定,请说明理由.14. 如图,∠AOB=90°,∠COD=60°. (1)、若OC平分∠AOD,求∠BOC的度数;(2)、若∠BOC=∠AOD,求∠AOD的度数;(3)、若同一平面内三条射线OT、OM、ON有公共端点O,且满足∠MOT=∠NOT或者∠NOT=∠MOT,我们称OT是OM和ON的“和谐线”.若射线OP从射线OB的位置开始,绕点O按逆时针方向以每秒12°的速度旋转,同时射线OQ从射线OA的位置开始,绕点O按顺时针方向以每秒9°的速度旋转,射线OP旋转的时间为t(单位:秒),且0<t<15,求当射线OP为两条射线OA和OQ的“和谐线”时t的值.15. 如图, .
(1)、若OC平分∠AOD,求∠BOC的度数;(2)、若∠BOC=∠AOD,求∠AOD的度数;(3)、若同一平面内三条射线OT、OM、ON有公共端点O,且满足∠MOT=∠NOT或者∠NOT=∠MOT,我们称OT是OM和ON的“和谐线”.若射线OP从射线OB的位置开始,绕点O按逆时针方向以每秒12°的速度旋转,同时射线OQ从射线OA的位置开始,绕点O按顺时针方向以每秒9°的速度旋转,射线OP旋转的时间为t(单位:秒),且0<t<15,求当射线OP为两条射线OA和OQ的“和谐线”时t的值.15. 如图, . (1)、试说明∠AOD与∠BOC互补;(2)、如图2,当射线OA、OB都在∠COD的外部时,过点O作射线OE、OF,若射线OE是∠BOE的三等分线(), , 求的度数:(3)、如图3,在(2)的条件下, , 射线OM平分∠EOD,过点O作射线ON,使 , 求的度数.16. 有两个形状、大小完全相同的直角三角板和 , 其中 . 将两个直角三角板和如图①放置,点A、C、E在直线上.
(1)、试说明∠AOD与∠BOC互补;(2)、如图2,当射线OA、OB都在∠COD的外部时,过点O作射线OE、OF,若射线OE是∠BOE的三等分线(), , 求的度数:(3)、如图3,在(2)的条件下, , 射线OM平分∠EOD,过点O作射线ON,使 , 求的度数.16. 有两个形状、大小完全相同的直角三角板和 , 其中 . 将两个直角三角板和如图①放置,点A、C、E在直线上. (1)、三角板位置不动,将三角板绕点C顺时针旋转一周,
(1)、三角板位置不动,将三角板绕点C顺时针旋转一周,①在旋转过程中,若 , 求得度数;
②在旋转过程中,与有怎样的数量关系?请依据图②说明理由.
(2)、在图①基础上,三角板和同时绕点C顺时针旋转,若三角板的边从处开始绕点C顺时针旋转,转速为10°/秒,同时三角板的边从处开始绕点C顺时针旋转,转速为1°/秒,当旋转一周再落到上时,两三角板都停止转动.如果设旋转时间为t秒,请结合图①完成在旋转过程中,当秒时,两三角板重合.在两三角板重合之前当秒时,有 .17. 操作与实践:在综合与实践活动课上,老师将一副三角板按图1所示的位置摆放,分别在∠AOC,∠BOD的内部作射线OM,ON,然后提出如下问题:先添加一个适当条件,再求∠MON的度数.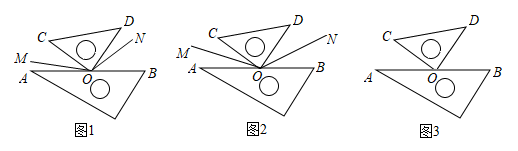 (1)、特例探究:“兴趣小组”的同学添加了:“若OM,ON分别平分∠AOC,∠BOD”,画出如图2所示图形.小组3号同学佳佳的做法:由于图中∠AOC与∠BOD的和为90°,所以我们容易得到∠MOC与∠NOD的和,这样就能求出∠MON的度数.请你根据佳佳的做法,写出解答过程.(2)、特例探究:“发现小组”的同学添加了:“若∠MOC=∠AOC,∠DON=∠BOD”,画出如图3所示图形.小组2号同学乐乐的做法:设∠AOC的度数为x°,我们就能用含有x°的式子表示出∠COM和∠DON的度数,这样就能求出∠MON的度数,请你根据乐乐的做法,写出解答过程.(3)、类比拓展:受“兴趣小组”和“发现小组”的启发,“创新小组”的同学添加了:“若∠MOC=∠AOC,∠DON=∠BOD”.请你直接写出∠MON的度数.18. 已知:如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=1:5.将一等腰直角三角板的直角顶点放在点O处,一直角边ON在射线OB上,另一直角边OM在直线AB的下方.
(1)、特例探究:“兴趣小组”的同学添加了:“若OM,ON分别平分∠AOC,∠BOD”,画出如图2所示图形.小组3号同学佳佳的做法:由于图中∠AOC与∠BOD的和为90°,所以我们容易得到∠MOC与∠NOD的和,这样就能求出∠MON的度数.请你根据佳佳的做法,写出解答过程.(2)、特例探究:“发现小组”的同学添加了:“若∠MOC=∠AOC,∠DON=∠BOD”,画出如图3所示图形.小组2号同学乐乐的做法:设∠AOC的度数为x°,我们就能用含有x°的式子表示出∠COM和∠DON的度数,这样就能求出∠MON的度数,请你根据乐乐的做法,写出解答过程.(3)、类比拓展:受“兴趣小组”和“发现小组”的启发,“创新小组”的同学添加了:“若∠MOC=∠AOC,∠DON=∠BOD”.请你直接写出∠MON的度数.18. 已知:如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=1:5.将一等腰直角三角板的直角顶点放在点O处,一直角边ON在射线OB上,另一直角边OM在直线AB的下方. (1)、将图1中的等腰直角三角板绕点O以每秒3°的速度逆时针方向旋转一周,直角边ON旋转后的对应边为ON',直角边OM旋转后的对应边为OM'.在此过程中,经过t秒后,OM'恰好平分∠BOC,求t的值;(2)、如图2,在(1)问的条件下,若等腰直角三角板在转动的同时,射线OC也绕点O以每秒4°的速度顺时针方向旋转,射线OC旋转后的对应射线为OC'.当射线OC'落在射线OC的反向延长线上时,射线OC和等腰直角三角板同时停止运动.在此过程中,是否存在某一时刻t,使得OC'//M'N'.若存在,请求出t的值,若不存在,诮说明理由;(3)、如图3,在(1)问的条件下,若等腰直角三角板在转动的同时,射线OC也绕点O以每秒5°的速度顺针方向旋转,射线OC旋转后的对应射线为OC'.当等腰直角三角板停止运动时,射线OC也停止运动.在整个运动过程中.经过l秒后,∠M'ON'的某一边恰好平分∠AOC',请直接写出所有满足条件的t的值.
(1)、将图1中的等腰直角三角板绕点O以每秒3°的速度逆时针方向旋转一周,直角边ON旋转后的对应边为ON',直角边OM旋转后的对应边为OM'.在此过程中,经过t秒后,OM'恰好平分∠BOC,求t的值;(2)、如图2,在(1)问的条件下,若等腰直角三角板在转动的同时,射线OC也绕点O以每秒4°的速度顺时针方向旋转,射线OC旋转后的对应射线为OC'.当射线OC'落在射线OC的反向延长线上时,射线OC和等腰直角三角板同时停止运动.在此过程中,是否存在某一时刻t,使得OC'//M'N'.若存在,请求出t的值,若不存在,诮说明理由;(3)、如图3,在(1)问的条件下,若等腰直角三角板在转动的同时,射线OC也绕点O以每秒5°的速度顺针方向旋转,射线OC旋转后的对应射线为OC'.当等腰直角三角板停止运动时,射线OC也停止运动.在整个运动过程中.经过l秒后,∠M'ON'的某一边恰好平分∠AOC',请直接写出所有满足条件的t的值.