2022~2023学年中考数学一轮复习专题12三角函数实际应用
试卷更新日期：2022-12-07 类型：一轮复习
一、坡度坡角问题
-
1. 2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情．如图是某滑雪场的横截面示意图，雪道分为AB，BC两部分，小明同学在C点测得雪道BC的坡度i=1：2.4，在A点测得B点的俯角∠DAB=30°．若雪道AB长为270m，雪道BC长为260m．
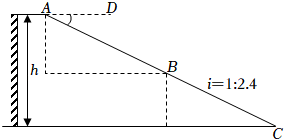(1)、求该滑雪场的高度h；(2)、据了解，该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求，其中甲设备每小时造雪量比乙设备少35m3 ， 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等．求甲、乙两种设备每小时的造雪量．2. 随着我国科学技术的不断发展，5G移动通信技术日趋完善．某市政府为了实现5G网络全覆盖，2021~2025年拟建设5G基站3000个，如图，在斜坡上有一建成的5G基站塔 ， 小明在坡脚处测得塔顶的仰角为 ， 然后他沿坡面行走了50米到达处，处离地平面的距离为30米且在处测得塔顶的仰角 ． （点、、、、均在同一平面内，为地平线）（参考数据： ， ， ）
(1)、求坡面的坡度；(2)、求基站塔的高．3. 某校数学兴趣小组为了测量建筑物 的高度，先在斜坡 的底部 测得建筑物顶点 的仰角为31°，再沿斜坡 走了 到达斜坡顶点 处，然后在点 测得建筑物顶点 的仰角为53°，已知斜坡 的坡度 .（参考数据： ， ）
(1)、求点 到地面的高度；(2)、求建筑物 的高度.4. 如图，一幢楼房后有一假山，其坡度为 ， 山坡坡面上E点处有一休息亭，测得假山坡脚C与楼房水平距离米，与亭子距离米，小丽从楼房顶测得E点的俯角为 ， 求楼房的高．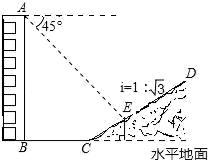
5. 如图，某旅游景点新建空中玻璃走廊PD，PD与建筑物AB垂直，在P处测得建筑物顶端A的仰角为37°，测得建筑物C处的仰角为26.6°，PD为54米．图中的点A、B、C、D、P及直线l均在同一平面内．
(1)、求A、C两点的高度差（结果精确到1米）；(2)、为方便游人，广场从地面l上的Q点新建扶梯PQ，PQ所在斜面的坡度 ， P到地面l的距离PE为10米．一公告牌MN位于EB的中点M处，为防止车辆阻塞，现要求在点Q右侧需留出12米宽的行车道，请判断是否需要挪走公告牌MN，并说明理由．（参考数据： ， ， ， ， ）6.某水库大坝的横截面是如图所示的四边形ABCD，其中AB∥CD，大坝顶上有一瞭望台PC，PC正前方有两艘渔船M，N．观察员在瞭望台顶端P处观测到渔船M的俯角α为31°，渔船N的俯角β为45°．已知MN所在直线与PC所在直线垂直，垂足为E，且PE长为30米．
(1)、求两渔船M，N之间的距离（结果精确到1米）；(2)、已知坝高24米，坝长100米，背水坡AD的坡度i=1：0.25，为提高大坝防洪能力，请施工队将大坝的背水坡通过填筑土石方进行加固，坝底BA加宽后变为BH，加固后背水坡DH的坡度i=1：1.75，施工队施工10天后，为尽快完成加固任务，施工队增加了机械设备，工作效率提高到原来的2倍，结果比原计划提前20天完成加固任务，施工队原计划平均每天填筑土石方多少立方米？（参考数据：tan31°≈0.60，sin31°≈0.52）
二、仰角俯角问题
-
7. 亚洲第一、中国唯一的航空货运枢纽一一鄂州花湖机场，于2022年3月19日完成首次全货运试飞，很多市民共同见证了这一历史时刻.如图，市民甲在C处看见飞机A的仰角为45°，同时另一市民乙在斜坡CF上的D处看见飞机A的仰角为30°，若斜坡CF的坡比=1：3，铅垂高度DG=30米（点E、G、C、B在同一水平线上）.求：
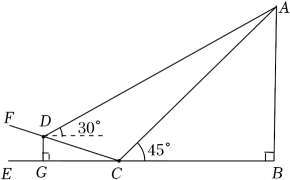(1)、两位市民甲、乙之间的距离CD；(2)、此时飞机的高度AB，（结果保留根号）8. 每年的11月9日是我国的“全国消防安全教育宣传日”，为了提升全民防灾减灾意识，某消防大队进行了消防演习．如图1，架在消防车上的云梯AB可伸缩（最长可伸至20m），且可绕点B转动，其底部B离地面的距离BC为2m，当云梯顶端A在建筑物EF所在直线上时，底部B到EF的距离BD为9m．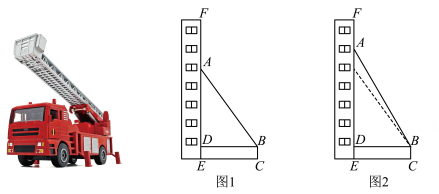
(参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3)
(1)、若∠ABD=53°，求此时云梯AB的长．(2)、如图2，若在建筑物底部E的正上方19m处突发险情，请问在该消防车不移动位置的前提下，云梯能否伸到险情处？请说明理由．9. 无人机在实际生活中应用广泛.如图8所示，小明利用无人机测量大楼的高度，无人机在空中P处，测得楼楼顶D处的俯角为 ， 测得楼楼顶A处的俯角为.已知楼和楼之间的距离为100米，楼的高度为10米，从楼的A处测得楼的D处的仰角为（点A，B，C，D、P在同一平面内）.
(1)、填空：度，度；(2)、求楼的高度（结果保留根号）；(3)、求此时无人机距离地面的高度.10. 我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔，是苏北地区现存最高和最古老的宝塔.小明与小亮要测量阿育王塔的高度，如图所示，小明在点 处测得阿育王塔最高点 的仰角 ，再沿正对阿育王塔方向前进至 处测得最高点 的仰角 ， ；小亮在点 处竖立标杆 ，小亮的所在位置点 、标杆顶 、最高点 在一条直线上， ， .
(1)、求阿育王塔的高度 ；(2)、求小亮与阿育王塔之间的距离 .（注：结果精确到 ，参考数据： ， ， ）
11. 已知甲楼AB高12米，自甲楼楼顶B处看乙楼楼顶D的仰角为25°，看乙楼楼底C的俯角为40°，现要在两楼楼顶B、D之间拉一条绳子挂小彩旗.（参考数据： ， ， ， ）
(1)、求乙楼CD的高度；（结果精确到1米）(2)、现有一条20米的绳子，请问是否够长？12. 如图，小明为了测量小河对岸大树BC的高度，他在点A测得大树顶端B的仰角为45°，沿斜坡走13米到达斜坡上点D，在此处测得树顶端点B的仰角为31°，且斜坡AF的坡度为1：2.4．
(1)、求小明从点A到点D的过程中，他上升的高度；(2)、大树BC的高度约为多少米？（参考数据：sin31°＝0.52，cos31°＝0.86，tan31°≈0.60）13. 交通安全心系千万家.高速公路管理局在某隧道内安装了测速仪，如图所示的是该段隧道的截面示意图.测速仪和测速仪到路面之间的距离 ， 测速仪和之间的距离 ， 一辆小汽车在水平的公路上由西向东匀速行驶，在测速仪处测得小汽车在隧道入口点的俯角为25°，在测速仪处测得小汽车在点的俯角为60°，小汽车在隧道中从点行驶到点所用的时间为38s（图中所有点都在同一平面内）.
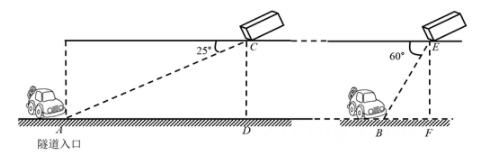(1)、求 ， 两点之间的距离（结果精确到1m）；(2)、若该隧道限速22m/s，判断小汽车从点行驶到点是否超速？通过计算说明理由.（参考数据： ， ， ， ， ， ）三、方向角问题
-
14. 湖中小岛上码头C处一名游客突发疾病，需要救援．位于湖面B点处的快艇和湖岸 A处的救援船接到通知后立刻同时出发前往救援．计划由快艇赶到码头 C 接该游客，再沿 CA方向行驶，与救援船相遇后将该游客转运到救援船上．已知 C 在A的北偏东 30°方向上，B在A的北偏东 60°方向上，且在C的正南方向 900米处．
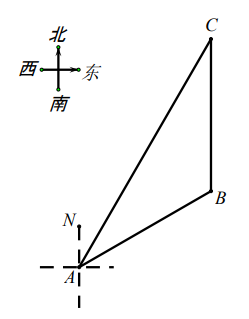(1)、求湖岸 A 与码头 C 的距离（结果精确到 1 米，参考数据： =1.732 ）；(2)、救援船的平均速度为 150 米/分，快艇的平均速度为 400 米/分，在接到通知后，快艇能否在5分钟内将该游客送上救援船？请说明理由．（接送游客上下船的时间忽略不计）15. 九年级二班学生到某劳动教育实践基地开展实践活动，当天，他们先从基地门口A处向正北方向走了220米，到达菜园B处锄草，再从B处沿正西方向走了200米，到达果园C处采摘水果，再向南偏东37°方向走了200米，到达手工坊D处进行手工制作，最后从D处回到门口A处．
(1)、求从手工坊D处回到门口A处的距离．(2)、求从手工坊D处回到门口A处的方位角．[参考数据： ， ， ]16. 如图，上午9时，一条船从A处出发，以每小时40海里的速度向正东方向航行，9时30分到达B处，从A，B两处分别测得小岛C在北偏东45°和北偏东15°．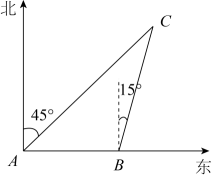
(1)、求∠C的度数；(2)、求B处船与小岛C的距离（结果保留根号）．17. 一段东西方向的海岸线MN上，小明从点A测得灯塔C位于北偏西15°方向，向东走300米到达点B处，测得灯塔C位于北偏西60°方向．
(1)、求点A到灯塔C的距离AC的长（结果保留根号）(2)、求灯塔C到海岸线MN的距离（结果保留根号）．18. 如图，正在执行巡航任务的海监船以每小时40海里的速度向正东方航行，在A处测得灯塔P在北偏东60°方向上，继续航行1小时到达B处，此时测得灯塔P在北偏东30°方向上．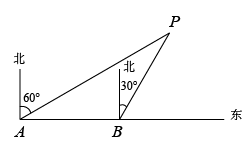
(1)、求的度数；(2)、已知在灯塔P的周围20海里内有暗礁，问海监船继续向正东方向航行是否安全？19. 小明学了《解直角三角形》内容后，对一条东西走向的隧道进行实地测量．如图所示，他在地面上点C处测得隧道一端点A在他的北偏东方向上，他沿西北方向前进米后到达点D，此时测得点A在他的东北方向上，端点B在他的北偏西方向上，（点A、B、C、D在同一平面内）
(1)、求点D与点A的距离；(2)、求隧道的长度．（结果保留根号）四、多边形构造解直角三角形函数问题
-
20. 2022年6月5日，“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射．如图是处于工作状态的某型号手臂机器人示意图，是垂直于工作台的移动基座，、为机械臂，m，m，m， ． 机械臂端点到工作台的距离m．
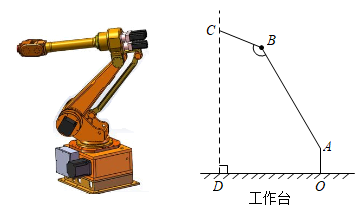(1)、求、两点之间的距离；(2)、求长．（结果精确到0.1m，参考数据： ， ， ， ）21. 为了监控危险路段的车辆行驶情况，通常会设置电子眼进行区间测速.如图电子眼位于点P处，离地面的铅垂高度PQ为11米；离坡AB的最短距离是11.2米，坡AB的坡比为3：4；电子眼照射在A 处时，电子眼的俯角为30°，电子眼照射在坡角点B处时，电子眼的俯角为70°.（A、B、P、Q在同一平面内）
(1)、求路段BQ的长；（sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）(2)、求路段AB的长；（≈1.7，结果保留整数）(3)、如图的这辆车看成矩形KLNM，车高2米，当PA过M点时开始测速，PB过M点时结束测速，若在这个测速路段车辆所用的时间是1.5秒.该路段限速5米/秒，计算说明该车是否超速？22. 如图1是2022年北京冬奥会首钢滑雪大跳台，曲线的设计灵感来自敦煌“飞天”飘带，又名“雪飞天”，它是世界上首例永久性保留和使用的滑雪大跳台场馆．如图2，为测量“雪飞天”的高度，测得大跳台跨度AB为140m，出发区CD为20m，且 ，AD为大跳台钢支架，在点A处测得点D的仰角∠DAB＝75°，在点C处测得点B的俯角∠ECB＝30°．（测角仪的高度忽略不计）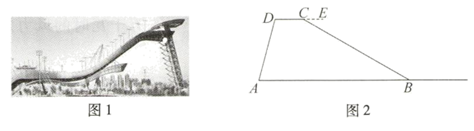
(1)、求大跳台出发区CD距离地面AB的高度．（结果精确到1m；参考数据： ， ， ， ）(2)、据了解，“雪飞天”需要造雪 ，分别用雪枪和雪炮来满足对于雪量和雪质的不同要求，雪炮出雪量大，适合室外滑雪场快速铺雪，雪枪造雪分布比较平均，相对造雪量比较小．若每台雪枪每小时出雪量比雪炮少 ，且一台雪枪出雪 所用的时间与一台雪炮出雪 所用的时间相等．求每台雪枪和雪炮每小时的出雪量．23. 图（1）为某大型商场的自动扶梯．图（2）中的AB为从一楼到二楼的扶梯的侧面示意图．小明站在扶梯起点A处时，测得天花板上日光灯C的仰角为37°，此时他的眼睛D与地面的距离AD＝1.8m，之后他沿一楼扶梯到达顶端B后又沿BL（ ）向正前方走了2m，发现日光灯C刚好在他的正上方．已知自动扶梯AB的坡度为1：2.4，AB的长度是13m，（参考数据：sin37°≈0.6，cos37°＝0.8，tan37°≈0.75）．
(1)、求图中B到一楼地面的高度．(2)、求日光灯C到一楼地面的高度．（结果精确到十分位）．24. 图1是某种手机支架在水平桌面上放置的实物图，图2是其侧面的示意图，其中支杆 ，可绕支点C，B调节角度，DE为手机的支撑面， ，支点A为DE的中点，且 ．
(1)、若支杆BC与桌面的夹角 ，求支点B到桌面的距离；(2)、在（1）的条件下，若支杆BC与AB的夹角 ，求支撑面下端E到桌面的距离．（结果精确到1cm，参考数据： ， ， ， ， ， ）25. 如图（1）是一种简易台灯，在其结构图（2）中灯座为△ABC（BC伸出部分不计），A、C、D在同一直线上.量得∠ACB＝90°，∠A＝60°，AB＝16cm，∠ADE＝150°，灯杆CD长为40cm，灯管DE长为16cm.
(1)、求DE与水平桌面（AB所在直线）所成的角；(2)、求台灯的高（点E到桌面的距离）.