2022~2023学年中考数学一轮复习专题11尺规作图设计
试卷更新日期:2022-12-07 类型:一轮复习
一、三角形作图(高,角平分线,中线及中垂线,平行线等)
-
1.
如图,已知△ABC,请用尺规过点A作一条直线,使其将△ABC分成面积相等的两部分.(保留作图痕迹,不写作法)
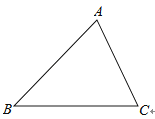 2. 如图,已知是的一个外角.请用尺规作图法,求作射线 , 使.(保留作图痕迹,不写作法)
2. 如图,已知是的一个外角.请用尺规作图法,求作射线 , 使.(保留作图痕迹,不写作法)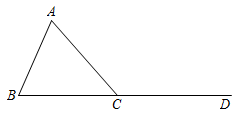 3. 如图,已知△ABC.
3. 如图,已知△ABC.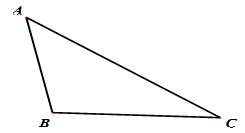
⑴作中线AD;
⑵尺规作出角平分线BE ;
⑶作BC边的高线.
4. 如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度直尺分别按下列要求画图(保留画图痕迹). (1)、在图1中,画出△ABD的BD边上的中线;(2)、在图2中,若BA=BD,画出△ABD的AD边上的高.5. 为了美化校园,某小区要在如图所示的三角形空地()上作一个半圆形花坛并使之满足以下要求;①圆心在边上,②该半圆面积最大.请你帮忙设计这一花坛.
(1)、在图1中,画出△ABD的BD边上的中线;(2)、在图2中,若BA=BD,画出△ABD的AD边上的高.5. 为了美化校园,某小区要在如图所示的三角形空地()上作一个半圆形花坛并使之满足以下要求;①圆心在边上,②该半圆面积最大.请你帮忙设计这一花坛.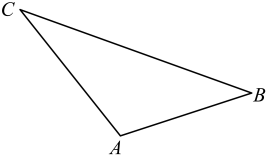 6.
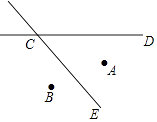
6.两个城镇A,B与一条公路CD,一条河流CE的位置如图所示,某人要修建一避暑山庄,要求该山庄到A,B的距离必须相等,到CD和CE的距离也必须相等,且在∠DCE的内部,请画出该山庄的位置P.(不要求写作法,保留作图痕迹.)
 7. 按要求作图,不要求写作法,但要保留作图痕迹.
7. 按要求作图,不要求写作法,但要保留作图痕迹.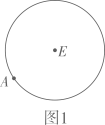
 (1)、如图1,A为圆E上一点,请用直尺(不带刻度)和圆规作出圆内接正方形;(2)、我们知道,三角形具有性质,三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高交于同一点,请运用上述性质,只用直尺(不带刻度)作图:
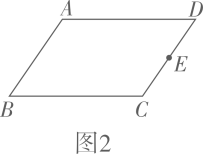
(1)、如图1,A为圆E上一点,请用直尺(不带刻度)和圆规作出圆内接正方形;(2)、我们知道,三角形具有性质,三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高交于同一点,请运用上述性质,只用直尺(不带刻度)作图:①如图2,在▱ABCD中,E为CD的中点,作BC的中点F;
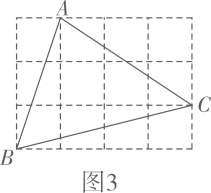
②图3,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作△ABC的高AH
8. 下面是小明同学设计的“过直线外一点作已知直线的平行线“的尺规作图过程.
已知:如图,直线 和直线 外一点 .
求作:直线 ,使直线 直线 .
作法:如图,

①在直线 上任取一点 ,作射线 ;
②以 为圆心, 为半径作弧,交直线 于点 ,连接 ;
③以 为圆心, 长为半径作弧,交射线 于点 ;分别以 为圆心,大于 长为半径作弧,在 的右侧两弧交于点 ;
④作直线 ;
所以直线 就是所求作的直线.
根据上述作图过程,回答问题:
(1)、用直尺和圆规,补全图中的图形;(2)、完成下面的证明:证明:由作图可知 平分 ,
.
又 ,
.( ▲ )(填依据1).
,
.
,∴直线 直线 .( ▲ )(填依据2).
二、平面直角坐标系作图(位似,轴对称,平移等)
-
9. 如图,在平面直角坐标系中,已知的三个顶点坐标分别是、、.

⑴请画出绕点顺时针旋转得到的;
⑵若点在线段上,且直线将分成面积相等的两部分,请画出线段 , 并写出的坐标.
10. 如图、在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,1),B(2,3),C(1,2).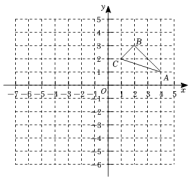
⑴画出与△ABC关于y轴对称的△A1B1C1;
⑵以原点O为位似中心,在第三象限内画一个△A2B2C2 , 使它与△ABC的相似比为 , 并写出点B2的坐标.
11. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标是A(0,﹣2),B(6,﹣4),C(2,﹣6).
⑴请画出与△ABC关于x轴对称的△A1B1C1.
⑵以点O为位似中心,将△ABC缩小为原来的 , 得到△A2B2C2 , 请在y轴左侧画出△A2B2C2.
⑶在y轴上存在点P,使得△OB2P的面积为6,请直接写出满足条件的点P的坐标.
12. 如图,在直角坐标系中,已知三个顶点的坐标分别为 , , . (1)、请画出与关于x轴对称的.(2)、以点O为位似中心,将缩小为原来的 , 得到 , 请在y轴的右侧画出.(3)、在y轴上存在点P,使得的面积为6,请直接写出满足条件的点P的坐标.13. 如图,在平面直角坐标系中,已知点 , 和 ,请按下列要求画图并填空.
(1)、请画出与关于x轴对称的.(2)、以点O为位似中心,将缩小为原来的 , 得到 , 请在y轴的右侧画出.(3)、在y轴上存在点P,使得的面积为6,请直接写出满足条件的点P的坐标.13. 如图,在平面直角坐标系中,已知点 , 和 ,请按下列要求画图并填空.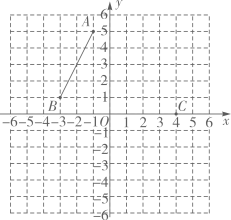
( 1 )平移线段 ,使点A平移到点C,画出平移后所得的线段 ,并写出点D的坐标为_▲_;
( 2 )将线段 绕点A逆时针旋转 ,画出旋转后所得的线段 ,并直接写出 的值为_▲_;
( 3 )在 轴上找出点 ,使 的周长最小,并直接写出点F的坐标为_▲__.
14. 如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系. (1)、画出四边形OABC关于y轴对称的四边形OA1B1C1 , 并写出点B1的坐标。(2)、画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2;连接OB,求出OB旋转到OB2所扫过部分图形的面积.15. 如图, 在平面直角坐标系中,顶点的坐标分别为 , , .
(1)、画出四边形OABC关于y轴对称的四边形OA1B1C1 , 并写出点B1的坐标。(2)、画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2;连接OB,求出OB旋转到OB2所扫过部分图形的面积.15. 如图, 在平面直角坐标系中,顶点的坐标分别为 , , . (1)、画出与 关于y轴对称的 ;(2)、将 绕点 顺时针旋转90°得到 , 弧是点A所经过的路径,则旋转中心 的坐标为.(3)、求图中阴影部分的面积(结果保留 ).
(1)、画出与 关于y轴对称的 ;(2)、将 绕点 顺时针旋转90°得到 , 弧是点A所经过的路径,则旋转中心 的坐标为.(3)、求图中阴影部分的面积(结果保留 ).三、网格作图
-
16. 如图在5×5的网格中,△ABC的顶点都在格点上.(仅用无刻度的直尺在给定的网格中按要求画图,画图过程用虚线表示,画图结果用实线表示)
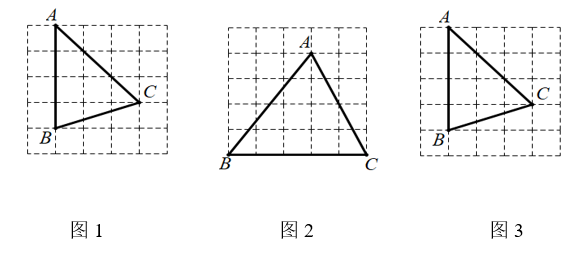 (1)、在图1中画出△ABC的中线AD;(2)、在图2中画线段CE,点E在AB上,使得 : =2 : 3;(3)、在图3中画出△ABC的外心点O.17. 图①,图②均是边长为1的小正方形组成的4×3的网格,每个小正方形的顶点称为格点,△ABC的顶点均在格点上,请用无刻度直尺按要求作图。
(1)、在图1中画出△ABC的中线AD;(2)、在图2中画线段CE,点E在AB上,使得 : =2 : 3;(3)、在图3中画出△ABC的外心点O.17. 图①,图②均是边长为1的小正方形组成的4×3的网格,每个小正方形的顶点称为格点,△ABC的顶点均在格点上,请用无刻度直尺按要求作图。 (1)、在图1中,作△ABC的中线CD;(2)、在图2中,作△ABC的高线AH。18. 图①、图②都是由边长为1的小等边三角形构成的网格, 为格点三角形.请仅用无刻度的直尺在网格中完成下列作图,不写作法,保留作图痕迹.
(1)、在图1中,作△ABC的中线CD;(2)、在图2中,作△ABC的高线AH。18. 图①、图②都是由边长为1的小等边三角形构成的网格, 为格点三角形.请仅用无刻度的直尺在网格中完成下列作图,不写作法,保留作图痕迹. (1)、在图①中,画出 中 边上的中线 ;(2)、在图②中,画出 中 边上的高 ,并直接写出 的面积.19. 如图均是5×5的正方形网络,每个小正方形的顶点称为格点, 的顶点 , , 都在格点上,按照下列要求画图.
(1)、在图①中,画出 中 边上的中线 ;(2)、在图②中,画出 中 边上的高 ,并直接写出 的面积.19. 如图均是5×5的正方形网络,每个小正方形的顶点称为格点, 的顶点 , , 都在格点上,按照下列要求画图. (1)、在图1中,画 的高 .(2)、在图2中,① ;
(1)、在图1中,画 的高 .(2)、在图2中,① ;②画以 为顶角的等腰三角形 ,使点 在格点上 .
(3)、在图3中,画出 的角平分线 .(要求:只用直尺,不能用圆规,不要求写出画法)
20. 如图,△ABC的顶点均为格点,AC与网格线交于点D.仅用无刻度尺的直尺在网格中画图,画图过程用虚线表示,画图结果用实线表示. (1)、如图1,画出△ABC的角平分线CE;(2)、如图1,平移AB至DN,使点A的对应点为点D;(3)、如图2,在AB上找一点G,使DG+CG最小;(4)、如图3,AB与网格线交于点E,过点E作EQ⊥AC于Q.21. 如图,在由小正方形组成的4×3的网格中,△ABC的顶点都在小正方形的顶点上,用无刻度的直尺,在所给的网格中,按要求作图并保留作图痕迹。
(1)、如图1,画出△ABC的角平分线CE;(2)、如图1,平移AB至DN,使点A的对应点为点D;(3)、如图2,在AB上找一点G,使DG+CG最小;(4)、如图3,AB与网格线交于点E,过点E作EQ⊥AC于Q.21. 如图,在由小正方形组成的4×3的网格中,△ABC的顶点都在小正方形的顶点上,用无刻度的直尺,在所给的网格中,按要求作图并保留作图痕迹。①在图1中作△ABC的轴对称图形△A'B'C';
②在图2中作△ABC的重心;
③在图3中作△ABC的的高线AH。
 22. 图①,图②均是的正方形网格,每个小正方形的顶点称为格点.其中点 , , 均在格点上.请在给定的网格中按要求画四边形.
22. 图①,图②均是的正方形网格,每个小正方形的顶点称为格点.其中点 , , 均在格点上.请在给定的网格中按要求画四边形.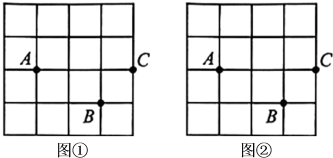 (1)、在图①中,找一格点 , 使以点 , , , 为顶点的四边形是轴对称图形;(2)、在图②中,找一格点 , 使以点 , , , 为顶点的四边形是中心对称图形.23. 如图所示,每个小正三角形的边长为1,且它的顶点叫做格点,各顶点在格点处的多边形称为格点多边形,线段AB位于该小正三角形组成的网格中,按要求在网格中作一个格点多边形.
(1)、在图①中,找一格点 , 使以点 , , , 为顶点的四边形是轴对称图形;(2)、在图②中,找一格点 , 使以点 , , , 为顶点的四边形是中心对称图形.23. 如图所示,每个小正三角形的边长为1,且它的顶点叫做格点,各顶点在格点处的多边形称为格点多边形,线段AB位于该小正三角形组成的网格中,按要求在网格中作一个格点多边形. (1)、请在图1画一个既是轴对称图形又是中心对称图形的四边形,且AB为对角线.(2)、请在图2中画一个以AB为边,面积为 的三角形.24. 在如图所示的6×6的网格中,每个小正方形的边长均为1个单位.
(1)、请在图1画一个既是轴对称图形又是中心对称图形的四边形,且AB为对角线.(2)、请在图2中画一个以AB为边,面积为 的三角形.24. 在如图所示的6×6的网格中,每个小正方形的边长均为1个单位.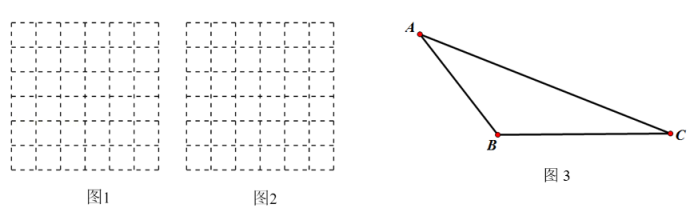 (1)、请你在图1中画一个以格点为顶点,面积为6个平方单位的等腰三角形:(2)、请你在图2中画一个以格点为顶点,一条直角边边长为的直角三角形.(3)、请你在图3中画出△ABC的边BC上的高AD,∠ACB的角平线CE
(1)、请你在图1中画一个以格点为顶点,面积为6个平方单位的等腰三角形:(2)、请你在图2中画一个以格点为顶点,一条直角边边长为的直角三角形.(3)、请你在图3中画出△ABC的边BC上的高AD,∠ACB的角平线CE四、新定义尺规作图题
-
25. 若两条线段将一个三角形分割成三个等腰三角形,则这两条线段称为三分线.
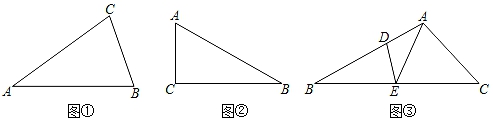 (1)、如图①,△ABC中,AB=AC,∠A=36°,请在图中画出两条三分线,并标出每个等腰三角形顶角的度数(画出一种分割即可).(2)、如图②,△ABC中,∠C=90°,∠A=60°,请在图中画出两条三分线,并标出每个等腰三角形顶角的度数(画出一种分割即可).(3)、如图③,△ABC中,∠BAC为钝角,AE,DE为三分线,BD=BE,DA=DE,CA=CE.
(1)、如图①,△ABC中,AB=AC,∠A=36°,请在图中画出两条三分线,并标出每个等腰三角形顶角的度数(画出一种分割即可).(2)、如图②,△ABC中,∠C=90°,∠A=60°,请在图中画出两条三分线,并标出每个等腰三角形顶角的度数(画出一种分割即可).(3)、如图③,△ABC中,∠BAC为钝角,AE,DE为三分线,BD=BE,DA=DE,CA=CE.①求∠B和∠C的关系式.
②求∠BAC的取值范围.
26. 实践操作(1)、如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)。
作∠BAC的平分线,交BC于点O;
(2)、以O为圆心,OC长为半径作圆。(3)、综合运用在你所作的图中,
AB与⊙O的位置关系是 (直接写出答案);
(4)、若AC=5,BC=12,求⊙O的半径。27. 数学活动课上,张老师组织同学们设计多姿多彩的几何图形, 下图都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影,请同学们在余下的空白小等边三角形中选取一个涂上阴影,使得4个阴影小等边三角形组成一个轴对称图形或中心对称图形,请画出4种不同的设计图形.规定:凡通过旋转能重合的图形视为同一种图形) 28. 如图,在每个小正方形的边长为1的网格中, 的顶点 均落在格点上,点B在网格线上,且 .
28. 如图,在每个小正方形的边长为1的网格中, 的顶点 均落在格点上,点B在网格线上,且 . (1)、线段 的长等于;(2)、以 为直径的半圆与边 相交于点D , 若 分别为边 上的动点,当 取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点 ,并简要说明点 的位置是如何找到的(不要求证明) .29. 如图是由小正方形组成的9×6网格,每个小正方形的顶点叫做格点.△ABC的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)、线段 的长等于;(2)、以 为直径的半圆与边 相交于点D , 若 分别为边 上的动点,当 取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点 ,并简要说明点 的位置是如何找到的(不要求证明) .29. 如图是由小正方形组成的9×6网格,每个小正方形的顶点叫做格点.△ABC的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.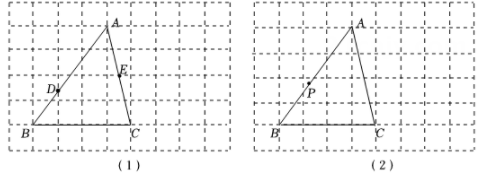 (1)、在图(1)中, , 分别是边 , 与网格线的交点.先将点绕点旋转得到点 , 画出点 , 再在上画点 , 使;(2)、在图(2)中,是边上一点,.先将绕点逆时针旋转 , 得到线段 , 画出线段 , 再画点 , 使 , 两点关于直线对称.
(1)、在图(1)中, , 分别是边 , 与网格线的交点.先将点绕点旋转得到点 , 画出点 , 再在上画点 , 使;(2)、在图(2)中,是边上一点,.先将绕点逆时针旋转 , 得到线段 , 画出线段 , 再画点 , 使 , 两点关于直线对称.