北师大版数学八年级上册《第一章 勾股定理》期末高分突破卷
试卷更新日期:2022-12-07 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 满足下列条件的△ABC不是直角三角形的是( )A、 B、 , , C、 D、2. 如图,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
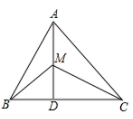 A、9 B、35 C、45 D、无法计算3. 一个直角三角形的两边长分别为4cm、3cm,则第三条边长为( )A、5cm B、4cm C、cm D、5cm 或cm4. 底边上的高为4,且底边长为12的等腰三角形周长为( )A、8+12 B、2+12 C、4+12 D、4+125. 如图将矩形ABCD沿对角线AC折叠,使D落在M处,AM与BC交于E,AB=4,AD=8,则BE长为( )
A、9 B、35 C、45 D、无法计算3. 一个直角三角形的两边长分别为4cm、3cm,则第三条边长为( )A、5cm B、4cm C、cm D、5cm 或cm4. 底边上的高为4,且底边长为12的等腰三角形周长为( )A、8+12 B、2+12 C、4+12 D、4+125. 如图将矩形ABCD沿对角线AC折叠,使D落在M处,AM与BC交于E,AB=4,AD=8,则BE长为( ) A、3 B、3.5 C、4 D、56. 如图,已知网格中每个小正方形的边长均为1,以点A为圆心,AB为半径画弧交网格线于点D,则ED的长为( )
A、3 B、3.5 C、4 D、56. 如图,已知网格中每个小正方形的边长均为1,以点A为圆心,AB为半径画弧交网格线于点D,则ED的长为( )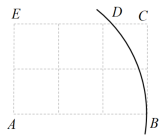 A、 B、3 C、2 D、7. 如图,直线l上有三个正方形,若a,c的面积分别为5和11,则b的面积为( )
A、 B、3 C、2 D、7. 如图,直线l上有三个正方形,若a,c的面积分别为5和11,则b的面积为( ) A、55 B、16 C、6 D、48. 如图,在△ABC中,∠ACB=90°,点D是AB的中点,连接CD,若AC=4,BC=3,则CD的长度是( )
A、55 B、16 C、6 D、48. 如图,在△ABC中,∠ACB=90°,点D是AB的中点,连接CD,若AC=4,BC=3,则CD的长度是( )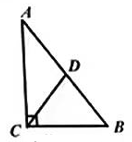 A、1.5 B、2 C、2.5 D、59. 如图,五根小木棒,其长度分别为5,9,12,13,15,现将它们摆成两个直角三角形,其中正确的是( )A、
A、1.5 B、2 C、2.5 D、59. 如图,五根小木棒,其长度分别为5,9,12,13,15,现将它们摆成两个直角三角形,其中正确的是( )A、 B、
B、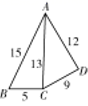 C、
C、 D、
D、 10. 有一个边长为1的正方形,以它的一条边为斜边,向外作一个直角三角形,再分别以直角三角形的两条直角边为边,向外各作一个正方形,称为第一次“生长”(如图1);再分别以这两个正方形的边为斜边,向外各自作一个直角三角形,然后分别以这两个直角三角形的直角边为边,向外各作一个正方形,称为第二次“生长”(如图2)……如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是( )
10. 有一个边长为1的正方形,以它的一条边为斜边,向外作一个直角三角形,再分别以直角三角形的两条直角边为边,向外各作一个正方形,称为第一次“生长”(如图1);再分别以这两个正方形的边为斜边,向外各自作一个直角三角形,然后分别以这两个直角三角形的直角边为边,向外各作一个正方形,称为第二次“生长”(如图2)……如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是( ) A、1 B、2020 C、2021 D、2022
A、1 B、2020 C、2021 D、2022二、填空题(每题3分,共15分)
-
11. 如图,等腰Rt△ABC的直角边长为4,D、E分别为边AB、AC上两个动点,且AE=BD,则CD+BE的最小值.
 12. 如图,AB⊥BC于点B,AB⊥AD于点小,点E是CD中点,若BC=5,AD=12,BE=12.5,则AB的长是
12. 如图,AB⊥BC于点B,AB⊥AD于点小,点E是CD中点,若BC=5,AD=12,BE=12.5,则AB的长是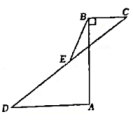 13. 下列条件:①∠C=∠A-∠B;②∠A:∠B:∠C=5∶2∶3;③a=c,b=c;④a∶b∶c=1∶2: , 则能确定△ABC是直角三角形的条件有个.14. 如图,一架秋千静止时,踏板离地的垂直高度DE=0.5m,将它往前推送1.5m(水平距离BC=1.5m)时,秋千的踏板离地的垂直高度BF=1m,秋千的绳索始终拉直,则绳索AD的长是 m.
13. 下列条件:①∠C=∠A-∠B;②∠A:∠B:∠C=5∶2∶3;③a=c,b=c;④a∶b∶c=1∶2: , 则能确定△ABC是直角三角形的条件有个.14. 如图,一架秋千静止时,踏板离地的垂直高度DE=0.5m,将它往前推送1.5m(水平距离BC=1.5m)时,秋千的踏板离地的垂直高度BF=1m,秋千的绳索始终拉直,则绳索AD的长是 m. 15. 如图,在长方形中, , . 点、点分别在、上,且 , 点是边上的动点,点是边上的动点.则的是小值是 .
15. 如图,在长方形中, , . 点、点分别在、上,且 , 点是边上的动点,点是边上的动点.则的是小值是 .
三、解答题(共9题,共75分)
-
16. 如图,将墙面和地平线的一部分分别标记 , , 且 . 把长为10m的梯子斜靠在墙上,梯子底端离墙角6m.如果梯子的顶端下滑了2m,求梯子底部在水平方向滑动的距离BD.
 17. 如图,在中,D为边上一点,已知 , , , . 请判断的形状,并求出的长.
17. 如图,在中,D为边上一点,已知 , , , . 请判断的形状,并求出的长. 18. 如图,甲船以16海里/时的速度离开港口,向东南航行,乙船在同时同地向西南方向航行,已知他们离开港口一个半小时后分别到达B、A两点,月知AB=30海里,问乙船每小时航行多少海里?
18. 如图,甲船以16海里/时的速度离开港口,向东南航行,乙船在同时同地向西南方向航行,已知他们离开港口一个半小时后分别到达B、A两点,月知AB=30海里,问乙船每小时航行多少海里? 19. 如图,∠AOB=90°,OA=40m,OB=15m.一机器人在B点处看见一球从A点出发沿AO方向匀速滚向O,机器人立即从B点出发,沿直线匀速前进栏截球,在C处截住球.球滚速与机器人行速相同,机器人行走的路程BC为多少?
19. 如图,∠AOB=90°,OA=40m,OB=15m.一机器人在B点处看见一球从A点出发沿AO方向匀速滚向O,机器人立即从B点出发,沿直线匀速前进栏截球,在C处截住球.球滚速与机器人行速相同,机器人行走的路程BC为多少? 20. 如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
20. 如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积. 21. 印度数学家什迦逻(1141年﹣1225年)曾提出过“荷花问题”:
21. 印度数学家什迦逻(1141年﹣1225年)曾提出过“荷花问题”:“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅”
请用学过的数学知识回答这个问题.
 22. 如图,一艘小船停留在点A处,在离水面高度为8米的台阶上有一根绳子连接小船,用绳子拉小船移动到点D处,已知开始时绳子的长米,停止后绳子的长米,求小船移动的距离的长.
22. 如图,一艘小船停留在点A处,在离水面高度为8米的台阶上有一根绳子连接小船,用绳子拉小船移动到点D处,已知开始时绳子的长米,停止后绳子的长米,求小船移动的距离的长.

