人教版数学八年级上册《第十一章 三角形》期末高分突破卷
试卷更新日期：2022-12-07 类型：复习试卷
一、单选题（每题3分，共30分）
-
1. 下列生活实例中，利用了“三角形稳定性”的是（ ）A、
B、
C、
D、
2. 下列各组图形中，表示AD是△ABC中BC边的高的图形为（ ）A、
B、
C、
D、
3. 若一个多边形的内角和是外角和的2倍，则这个多边形是（ ）A、五边形 B、六边形 C、七边形 D、八边形4. 在△ABC中，三边长分别为a、b、c ， 且a＞b＞c ， 若b=8，c=3，则a的取值范围是（ ）A、3＜a＜8 B、5＜a＜11 C、6＜a＜10 D、8＜a＜115. 如下图，等于（ ）
A、90° B、120° C、180° D、360°6. 如图，将三角板的直角放置在内，恰好三角板的两条直角边分别经过点B，C．若 ， 则 =（ ）
A、35 B、45 C、55 D、607. 如图，为估计池塘两岸间的距离，小明在池塘一侧选取点M，测得 ， ， 那么间的距离不可能是（ ）
A、 B、 C、 D、8. 如图，在△ABC中，AD是角平分线，AE是高，已知∠B=50°，∠C=60°，那么∠EAD的度数为（ ）
A、5° B、15° C、25° D、35°9. 如图，在中，已知点D、E、F分别为的中点，且 ， 则阴影部分面积S是（ ）
A、1 B、2 C、3 D、410. 如图，在△ABC中，AD是BC边上的高，且∠ACB＝∠BAD，AE平分∠CAD，交BC于点E，过点E作EFAC，分别交AB、AD于点F、G则下列结论：①∠BAC＝90°；②∠AEF＝∠BEF；③∠BAE＝∠BEA；④∠B＝2∠AEF，其中正确的有（ ）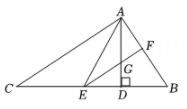
A、①③④ B、①②③ C、①③ D、①②③④二、填空题（每题3分，共15分）
-
11. 如图所示，在Rt中，是斜边上的高， ， 则度.
12. 如图，是A、B、C三个村庄的平面图，已知B村在A村的南偏西50°方向，C村在A村的南偏东15°方向，C村在B村的北偏东85°方向，则从C村观测A、B两村的视角∠ACB的度数为。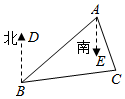
13. 如图，是的外角的平分线，若 ， ， 则的度数是.
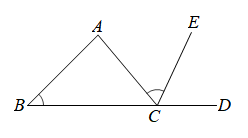14. 已知D、E分别是△ABC的边BC和AC的中点，若△ABC的面积=36cm ， 则△DEC的面积为 ．
15. 如图，在 中， ，将 平移5个单位长度得到 1，点P、Q分别是 、 的中点， 的最小值等于 ．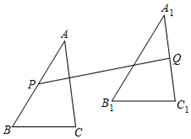
三、解答题（共8题，共75分）
-
16. 如图，AD为△ABC的中线，BE为△ABD的中线．若△ABC的面积为40，BD=5，则△BDE中BD边上的高为多少？
17. 已知：△ABC中，AB＝AC，BD是AC边上的中线，如果D点把三角形ABC的周长分为12cm和15cm两部分，求此三角形各边的长．18. 如图，在△ABC中，AE，CD分别是∠BAC， ∠ACB的平分线，且AE，CD相交于点F.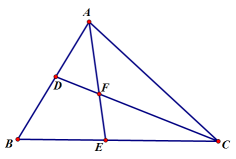
(1)、若∠BAC=80°，∠ACB=40°，求∠AFC的度数；(2)、若∠B=80°，求∠AFC的度数；(3)、若∠B=x°，用含x的代数式表示∠AFC的度数.19. 如图，AD为△ABC的高，AE、BF为△ABC的角平分线，若 ， ．
(1)、求∠DAE的度数；(2)、若点M为线段BC上任意一点，当△BMF为直角三角形时，请直接写出∠CFM的度数．20. 看对话答题：小梅说：这个多边形的内角和等于1125°
小红说：不对，你少加了一个角
问题：
(1)、他们在求几边形的内角和?(2)、少加的那个内角是多少度?21. 已知：如图 ，与点 不重合的两点 、 分别在 、 上， 平分 ， 所在的直线与 的平分线所在的直线相交于点 .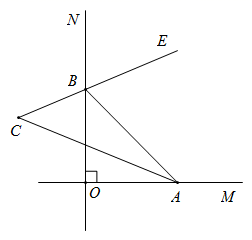
(1)、当点 、 分别在射线 、 上，且 时，求 的度数；(2)、当点 、 分别在射线 、 上运动时， 的大小是否发生变化？若不变，请给出证明；若发生变化，请求出 的范围.22. 如图①，∠1、∠2是四边形ABCD的两个不相邻的外角．
(1)、猜想并说明∠1+∠2与∠A、∠C的数量关系；(2)、如图②，在四边形ABCD中，∠ABC与∠ADC的平分线交于点O．若∠A＝58°，∠C＝152°，求∠BOD的度数；(3)、如图③，BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线．请直接写出∠A、∠C与∠O的数量关系．23. 如图（1）所示的图形，像我们常见的学习用品一圆规，我们常把这样的图形叫做“规形图”．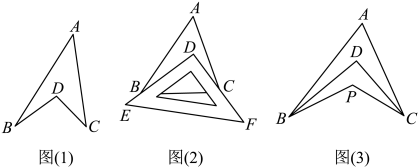
(1)、观察“规形图”，试探究与、、之间的数量关系，并说明理由；(2)、请你利用此结论，解决以下两个问题：①如图（2），把一个三角尺放置在上，使三角尺的两条直角边 ， 恰好经过点 ， ， 若 ， 则 ▲ ；
②如图（3），平分 ， 平分 ， 若 ， ， 求的度数．