华师大版数学八年级上册《第13章 全等三角形》期末高分突破卷
试卷更新日期:2022-12-07 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 等腰三角形的一个角为80°,则它的顶角度数是( )A、20° B、80° C、20°或80° D、无法确定2. 如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充的条件是( )
 A、AC=AD或BC=BD B、AC=AD且BC=BD C、∠BAC=∠BAD D、以上都不对3. 下列说法正确的是( )A、形状相同的两个三角形全等 B、面积相等的两个三角形全等 C、所有的等腰三角形都全等 D、完全重合的两个三角形全等4. 如图,直线l1 , l2 , l3表示三条公路。现要建造一个洗手台P,使P到三条公路的距离都相等,则洗手台P可选择的点有( )
A、AC=AD或BC=BD B、AC=AD且BC=BD C、∠BAC=∠BAD D、以上都不对3. 下列说法正确的是( )A、形状相同的两个三角形全等 B、面积相等的两个三角形全等 C、所有的等腰三角形都全等 D、完全重合的两个三角形全等4. 如图,直线l1 , l2 , l3表示三条公路。现要建造一个洗手台P,使P到三条公路的距离都相等,则洗手台P可选择的点有( ) A、一处 B、二处 C、三处 D、四处5. 如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
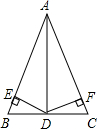
A、一处 B、二处 C、三处 D、四处5. 如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( ) A、 B、 C、 D、6. 如图,DE=11,FG=3,BF、CG分别平分∠ABC、∠ACB,DE∥BC.
A、 B、 C、 D、6. 如图,DE=11,FG=3,BF、CG分别平分∠ABC、∠ACB,DE∥BC.则BD+CE=( )
 A、3 B、11 C、7 D、87. 下列命题是真命题的是( )A、两个等边三角形一定全等 B、形状相同的两个三角形全等 C、全等三角形的面积一定相等 D、面积相等的两个三角形全等8. 如图,中,分别平分和 , 过点F作交于点D,交于点E,那么下列结论:
A、3 B、11 C、7 D、87. 下列命题是真命题的是( )A、两个等边三角形一定全等 B、形状相同的两个三角形全等 C、全等三角形的面积一定相等 D、面积相等的两个三角形全等8. 如图,中,分别平分和 , 过点F作交于点D,交于点E,那么下列结论:①;②为等腰三角形;③的周长等于的周长;④.其中正确的是( )
 A、①② B、①③ C、①②④ D、①②③④
A、①② B、①③ C、①②④ D、①②③④二、填空题(每题3分,共15分)
-
9. 已知等腰三角形的一边长等于4,一边长等于8,则它的周长为.10. 如图,中, , 点D在上,且于点E , , 若 , 则.
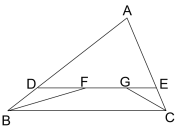
 11. 如果等腰三角形的周长是27cm,一腰上的中线把三角形分成两个三角形,其周长之差是3cm,则这个等腰三角形的底边长为cm。12. 如图,已知 , , E,F分别是线段和射线上的动点,且 , 点G在射线上,连接 , 若与全等,则线段的长为 .
11. 如果等腰三角形的周长是27cm,一腰上的中线把三角形分成两个三角形,其周长之差是3cm,则这个等腰三角形的底边长为cm。12. 如图,已知 , , E,F分别是线段和射线上的动点,且 , 点G在射线上,连接 , 若与全等,则线段的长为 . 13. 如图,已知点B是直线MN外一点,A是直线MN上一点,且∠BAN=20°,点P是直线MN上一动点,当△ABP是等腰三角形时,它的顶角的度数为 .
13. 如图,已知点B是直线MN外一点,A是直线MN上一点,且∠BAN=20°,点P是直线MN上一动点,当△ABP是等腰三角形时,它的顶角的度数为 .
三、解答题(共8题,共75分)
-
14. 如图,在中, , , 垂足分别为点D,E,与相交于点F.若点F在的平分线上,判断的形状,并说明理由.
 15. 如图,在中, , 点D是线段上一点,以为腰作等腰直角 , 使 , 于点G,交于点F.求证: .
15. 如图,在中, , 点D是线段上一点,以为腰作等腰直角 , 使 , 于点G,交于点F.求证: . 16. 如图,在△ABD和△ACE中,有下列四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.请你以其中三个等式作为题设,余下的作为结论,写出一个正确的结论(要求写出已知,求证及证明过程)
16. 如图,在△ABD和△ACE中,有下列四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.请你以其中三个等式作为题设,余下的作为结论,写出一个正确的结论(要求写出已知,求证及证明过程)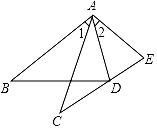 17. 如图,是的高,平分交于E.若 , , 求的度数.
17. 如图,是的高,平分交于E.若 , , 求的度数. 18. 如图,已知.
18. 如图,已知. (1)、用直尺和圆规,作出线段的垂直平分线(不写作法,保留作图痕迹)(2)、如果线段的垂直平分线交于点D , 连结 , 已知 , 求的度数.19. 上数学活动课时,欢欢为测量池塘两端A、B的距离,设计了如下方案:
(1)、用直尺和圆规,作出线段的垂直平分线(不写作法,保留作图痕迹)(2)、如果线段的垂直平分线交于点D , 连结 , 已知 , 求的度数.19. 上数学活动课时,欢欢为测量池塘两端A、B的距离,设计了如下方案:
(1)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(2)如图2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.阅读后回答下列问题:
(1)、方案(1)是否可行?请说明理由.(2)、方案(2)是否可行?请说明理由.(3)、方案(2)若仅满足∠ABD=∠BDE≠90°,BC=CD,方案(2)(填“可行”或“不可行”).