天津市北辰区2022-2023学年八年级上学期期中数学试卷
试卷更新日期:2022-12-06 类型:期中考试
一、单选题
-
1. 2022年冬奥会在北京举行,以下历届冬奥会会徽是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三条线段,能组成三角形的是( )A、3,4,8 B、5,6,10 C、5,5,11 D、5,6,113. 如图,直线 ,且 于点 ,若 ,则 的度数为( )
2. 下列长度的三条线段,能组成三角形的是( )A、3,4,8 B、5,6,10 C、5,5,11 D、5,6,113. 如图,直线 ,且 于点 ,若 ,则 的度数为( )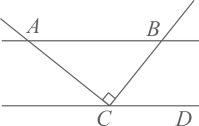 A、65° B、55° C、45° D、35°4. 若画△ABC中AB边上的高,下列画法中正确的是( )A、
A、65° B、55° C、45° D、35°4. 若画△ABC中AB边上的高,下列画法中正确的是( )A、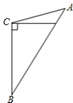 B、
B、 C、
C、 D、
D、 5. 如图,一棵树在一次强台风中,从离地面5m处折断,倒下的部分与地面成30°角,这棵树在折断前的高度是( )
5. 如图,一棵树在一次强台风中,从离地面5m处折断,倒下的部分与地面成30°角,这棵树在折断前的高度是( )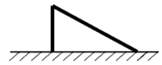 A、5m B、10m C、15m D、20m6. 用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A、5m B、10m C、15m D、20m6. 用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
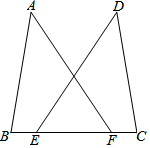
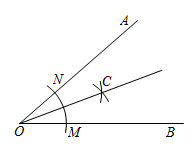 A、SSS B、ASA C、AAS D、SAS7. 如图,AB=AC,AD=AE,下列结论错误的是( )
A、SSS B、ASA C、AAS D、SAS7. 如图,AB=AC,AD=AE,下列结论错误的是( ) A、∠B=∠C B、BD=CE C、BE⊥CD D、△ABE≌△ACD8. 如图, , , ,则 的度数为( )
A、∠B=∠C B、BD=CE C、BE⊥CD D、△ABE≌△ACD8. 如图, , , ,则 的度数为( ) A、20° B、25° C、30° D、35°9. 如图,若平分 , 垂足分别是、 , 则下列结论中错误的是( )
A、20° B、25° C、30° D、35°9. 如图,若平分 , 垂足分别是、 , 则下列结论中错误的是( ) A、 B、、不一定相等 C、 D、10. 将一副三角尺按如图所示的方式摆放,则 的大小为( )
A、 B、、不一定相等 C、 D、10. 将一副三角尺按如图所示的方式摆放,则 的大小为( ) A、 B、 C、 D、11. 如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )
A、 B、 C、 D、11. 如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )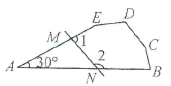 A、210° B、110° C、150° D、100°12. 如图,在 中, ,垂足为D, 与 关于直线AD对称,点的B对称点是 ,则 的度数是( )
A、210° B、110° C、150° D、100°12. 如图,在 中, ,垂足为D, 与 关于直线AD对称,点的B对称点是 ,则 的度数是( )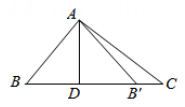 A、 B、 C、 D、13. 如图,在中, , 线段的垂直平分线交 , 于点、 , 的周长是 , 则的长为( )
A、 B、 C、 D、13. 如图,在中, , 线段的垂直平分线交 , 于点、 , 的周长是 , 则的长为( ) A、 B、 C、 D、14. 在ABC中,AB=AC,D为BC上一点,DA=DC,BD=BA,则∠B的大小为( )
A、 B、 C、 D、14. 在ABC中,AB=AC,D为BC上一点,DA=DC,BD=BA,则∠B的大小为( ) A、40° B、36° C、30° D、35°15. 如图,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED ;②AC+ BE= AB ;③DA平分∠CDE ;④∠BDE =∠BAC;⑤=AB:AC,其中结论正确的个数有( )
A、40° B、36° C、30° D、35°15. 如图,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED ;②AC+ BE= AB ;③DA平分∠CDE ;④∠BDE =∠BAC;⑤=AB:AC,其中结论正确的个数有( ) A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
16. 点P(2,3)关于y轴的对称点Q的坐标为17. 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .18. 如图,自行车的车身为三角形结构,这样做根据的数学道理是.
 19. 如图,已知 ,添加下列条件中的一个:① ,② ,③ ,其中不能确定 ≌△ 的是(只填序号).
19. 如图,已知 ,添加下列条件中的一个:① ,② ,③ ,其中不能确定 ≌△ 的是(只填序号).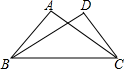 20. 如图,是的中线,是的中线,若 , 则 .
20. 如图,是的中线,是的中线,若 , 则 .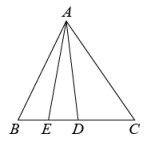 21. 如图,中,、分别为、的中点, , 则阴影部分的面积是.
21. 如图,中,、分别为、的中点, , 则阴影部分的面积是. 22. 如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是 .
22. 如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是 . 23. 如图.在 中, , .若 ,则 .
23. 如图.在 中, , .若 ,则 .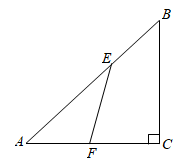 24. 如图,△ABC中,∠A=55°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DB的度数为 .
24. 如图,△ABC中,∠A=55°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DB的度数为 .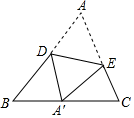 25. 如图,在△ABC中,AB=AC=10cm,BC=8cm,AB的垂直平分线交AB于点M,交AC于点N,在直线MN上存在一点P,使P、B、C三点构成的△PBC的周长最小,则△PBC的周长最小值为 .
25. 如图,在△ABC中,AB=AC=10cm,BC=8cm,AB的垂直平分线交AB于点M,交AC于点N,在直线MN上存在一点P,使P、B、C三点构成的△PBC的周长最小,则△PBC的周长最小值为 .
三、解答题
-
26. 如图,中,是的一条角平分线,求和的度数.
 27. 如图 , , , 求和的度数.
27. 如图 , , , 求和的度数. 28. 如图,AB平分∠CAD,AC=AD.求证:BC=BD.
28. 如图,AB平分∠CAD,AC=AD.求证:BC=BD.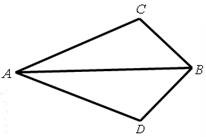 29. 如图,求证: .
29. 如图,求证: .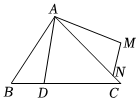 30. 如图,点 , 在 上, , , ,求证: .
30. 如图,点 , 在 上, , , ,求证: .