上海市黄浦区2022-2023学年八年级上学期期中考试数学试题

试卷更新日期：2022-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{a b^{3}}$ 、 $\sqrt{a^{2} + 1}$ 、 $\sqrt{\frac{b}{5}}$ 、 $\frac{\sqrt{3}}{2}$ 中最简二次根式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列二次根式中与 $\sqrt{a + 1}$ 互为有理化因式的是（）

A、 $\sqrt{1 - a}$ B、 $\sqrt{a} - 1$ C、 $\sqrt{1 + a}$ D、 $\sqrt{a} + 1$

查看试题解析
3. 下列函数（其中x是自变量）中，一定是正比例函数的是（）

A、 $y = \frac{2}{x}$ B、 $y = - \frac{x}{3}$ C、 $y = - 3 x + 2$ D、 $y = k x$

查看试题解析
4. 关于 $x$ 的方程 $k x^{2} - k x = 5 - 3 x^{2}$ 是一元二次方程的条件是（）

A、 $k \neq 0$ B、 $k \neq 1$ C、 $k \neq 3$ D、 $k \neq - 3$

查看试题解析
5. 下列方程中，无实数根的方程为（）

A、 $2 x^{2} + 6 x = 3$ B、 $3 x^{2} + 4 x + 6 = 0$ C、 $x^{2} - 2 x = 0$ D、 $3 x^{2} - 4 x - 6 = 0$

查看试题解析
6. 下列问题中两个变量成正比例的是（）

A、正方形面积和它的边长 B、一条边确定的长方形，其周长与另一边长 C、圆的面积与它的半径 D、半径确定的圆中，弧长与该弧长所对圆心角的度数

查看试题解析

二、填空题

7. 化简： $\sqrt{28}$ =.

查看试题解析
8. 方程 $- x^{2} + 5 x + 6 = 0$ 的解为．

查看试题解析
9. 函数y= $\frac{x - 5}{\sqrt{x + 3}}$ 的定义域为．

查看试题解析
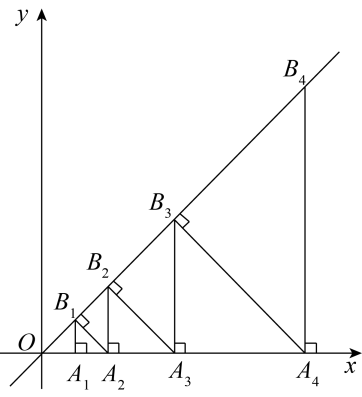
10. $\sqrt{2 a} - \sqrt{b}$ 的一个有理化因式是．

查看试题解析
11. 若最简二次根式 $\sqrt{1 - 2 a}$ 和 $\sqrt[b - 1]{7}$ 是同类二次根式，那么a+b的值是．

查看试题解析
12. 写出一个一元二次方程，使它的一个根为1，另一个根为 $- \sqrt{2}$ ，这个方程的一般式是．

查看试题解析
13. 在实数范围内分解因式： $3 x^{2} - x - 1 =$ ．

查看试题解析
14. 如果正比例函数 $y = (k - 2) x$ 的图像y随x的减小而增大，那么k的取值范围是．

查看试题解析
15. 市政府为了解决市民看病难的问题，决定下调药品的价格．某种药品原来每盒200元，经过两次降价，每次降价的百分率相同，现在每盒售价128元，则这种药品每次降价的百分率为．

查看试题解析
16. 等腰三角形的周长是10厘米，腰长是 $x$ 厘米，底边长是 $y$ 厘米，请写出 $y$ 关于 $x$ 的函数关系式，并写出自变量 $x$ 的取值范围．

查看试题解析
17. 定义：若两个一元二次方程有且只有一个相同的实数根，我们就称这两个方程为“同伴方程”．例如 $x^{2} = 4$ 和 $(x - 2) (x + 3) = 0$ 有且仅有一个相同的实数根 $x = 2$ ，所以这两个方程为“同伴方程”．若关于x的方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的参数同时满足 $a + b + c = 0$ 和 $a - b + c = 0$ ，且该方程与 $(x + 2) (x - n) = 0$ 互为“同伴方程”，则 $n =$ ．

查看试题解析
18. 如图，在平面直角坐标系中，点A₁ ， A₂ ， A₃…都在x轴上，点B₁ ， B₂ ， B₃…都在直线y＝x上， $△$ OA₁B₁ ， $△$ B₁A₁A₂ ， $△$ B₂B₁A₂ ， $△$ B₂A₂A₃ ， $△$ B₃B₂A₃…都是等腰直角三角形，且OA₁＝1，则点B₂₀₂₂的坐标是．

查看试题解析

三、解答题

19. 计算： $2 \sqrt{2} \times 3 \sqrt{10} + \sqrt{45} + \sqrt{1 \frac{1}{4}} - \frac{1}{2 - \sqrt{5}}$ ．

查看试题解析
20. 计算： $\frac{2}{m} \sqrt{m^{2} n} \times (\frac{3}{2} \sqrt{m n^{2}}) \div (\frac{1}{3} \sqrt{\frac{m}{n}}) \begin{matrix} (m > 0) \end{matrix}$ ．

查看试题解析
21. 解方程： ${(x + 1)}^{2} = 4 x$ ．

查看试题解析
22. 解方程： $\frac{1}{2} x^{2} - 2 x - 3 = 0$ ．

查看试题解析
23. 解方程： $\sqrt{2} {(x - 1)}^{2} + \sqrt{3} (1 - x) = 0$ ．

查看试题解析
24. 已知y与 $x - 1$ 成正比例，且当 $x = - 2$ 时， $y = \frac{3}{4}$ ．

(1)、求y与x的函数解析式．

(2)、请判断点 $(5 ， - 1)$ 是否在此函数上，请说明理由．

查看试题解析
25. 已知关于的x方程 $4 x^{2} - (k + 2) x + k = 1$ 有两个相等的实数根，求k的值及这时方程的根.

查看试题解析
26. 如图，在甲、乙两名同学进行400米跑步比赛中，路程S（米）与时间（t）之间的函数关系的图像分别为折线OAB和线段OC请根据图上信息回答下列问题

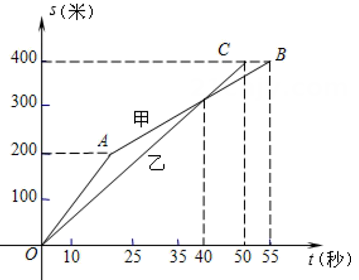(1)、先到达终点；

(2)、第秒时，追上；

(3)、比赛过程中，的速度适中保持不变；

(4)、优胜者在比赛过程中所跑的路程S（米）关于时间t（秒）的函数解析式及定义域为 .

查看试题解析
27. 第二十二届中国上海国际艺术节首次移师上海市黄浦区南京东路第一百货商业中心．主办方工作人员准备利用一边靠墙（墙长25米）的空旷场地为提前到场的观众设立面积为320平方米的封闭型长方形等候区．如图，为了方便观众进出，在两边空出两个宽各为1米的出入口，共用去隔栏绳50米．请问，工作人员围成的这个长方形的相邻两边长分别是多少米？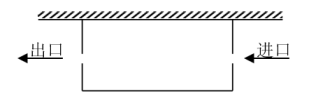

解：令这个长方形垂直于墙的一边为宽，平行于墙的一边为长；

设这个长方形的宽为 $x$ 米，则长为 ▲ 米．（用含x代数式表示）

（完成填空后继续解题）

查看试题解析
28. 已知：如图，直线 $y = 2 x$ 上有一点 $P (2 ， a)$ ，直线 $y = k x (0 < k < 1)$ 上有一点 $Q (b ， 2)$ ．

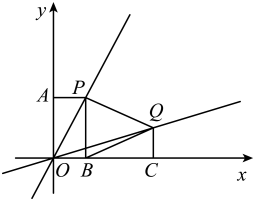(1)、求点P和点Q的坐标（其中点Q的坐标用含k的代数式表示）．

(2)、过点P分别作 $P A ⊥ y$ 轴， $P B ⊥ x$ 轴，过点Q分别作 $Q C ⊥ x$ 轴，如果 $△ O P Q$ 的面积等于 $△ B P Q$ 的面积的两倍，请求出k的值．

(3)、在（2）的条件下，在直线 $O Q$ 上是否存在点 $D$ ，使 $S_{△ O C D} = 12$ ？如果存在，请求出点 $D$ 的坐标；如果不存在，请说明理由．

查看试题解析