吉林省长春市汽开区2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $a^{3} \cdot a^{3} = 2 a^{3}$ B、 $x^{2} + x^{2} = x^{4}$ C、 $3 x^{2} \div 2 x = x$ D、 ${(b^{3})}^{2} = b^{6}$

查看试题解析
2. 在实数 $\sqrt{2}$ ， $\frac{π}{3}$ ， 0.3131131113…，−3.14中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 在数轴上，与 $\sqrt{23} - 2$ 最接近的整数是（）

A、2 B、3 C、4 D、5

查看试题解析
4. 下列各式中，运算结果是 $9 a^{2} - 16 b^{2}$ 的是（）

A、 $(3 a + 2 b) (3 a - 8 b)$ B、 $(- 4 b + 3 a) (- 4 b - 3 a)$ C、 $(- 3 a + 4 b) (- 3 a - 4 b)$ D、 $(4 b + 3 a) (4 b - 3 a)$

查看试题解析
5. 用一条长为18cm的细绳围成一个等腰三角形，若其中有一边的长为5cm，则该等腰三角形的腰长为（）cm

A、5 B、6.5 C、5或6.5 D、6.5或8

查看试题解析
6. 如图，在△ABC中，∠A＝45°，∠B＝60°，点D在边AB上，且BD＝BC，连接CD，则∠ACD的大小为（）

A、30° B、25° C、15° D、10°

查看试题解析
7. 如图，已知一条线段的长度为a，作边长为a的等边三角形的方法是：①画射线AM；②连结AC、BC；③分别以A、B为圆心，以a的长为半径作圆弧，两弧交于点C；④在射线AM上截取AB＝a；以上画法正确的顺序是（）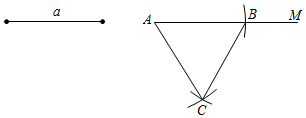

A、①②③④ B、①④③② C、①④②③ D、②①④③

查看试题解析
8. 有两个正方形 $A ， B$ ，现将 $B$ 放在 $A$ 的内部得图甲，将 $A ， B$ 并列放置后构造新的正方形得图乙，若图甲和图乙中阴影部分的面积分别为3和16，则正方形 $A ， B$ 的面积之和为（）

A、13 B、11 C、19 D、21

查看试题解析

二、填空题

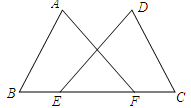
9. -0.008的立方根是。

查看试题解析
10. 计算 $(2 a - b)$ （） $= 4 a^{2} - b^{2}$

查看试题解析
11. 分解因式： $9 x^{2} - y^{2} =$ ．

查看试题解析
12. 当 $a = 3 ， a - b = 1$ 时，代数式 $a^{2} - a b$ 的值是．

查看试题解析
13. 如图，在△ABC中，AB＝AC，点D、E在BC的延长线上，G是AC上一点，且CG＝CD，F是GD上一点，且DF＝DE．若∠A＝100°，则∠E的大小为度．

查看试题解析
14. 如图， $∠ B O C = 60 °$ ， A是BO的延长线上一点， $O A = 12 cm$ ，动点P从点A出发，沿AB以2cm/s的速度移动，动点Q从点O出发沿OC以1cm/s的速度移动，若点P、Q同时出发，当 $△ O P Q$ 是等腰三角形时，移动的时间是．

查看试题解析

三、解答题

15. 计算：

(1)、 $| - 5 | + \sqrt{16} - 3^{2}$ ．

(2)、 ${(- \frac{1}{2})}^{2} + \sqrt[3]{8} - | 1 - \sqrt{9} |$ ．

查看试题解析
16. 因式分解：

(1)、 $- x^{5} y^{3} + x^{3} y^{5}$ ；

(2)、 $2 x^{2} - 4 x + 2$ ．

查看试题解析
17. 计算：

(1)、 ${(- 2 a)}^{2} \cdot (a - 1)$

(2)、 $(2 x + 1) (2 x + 5)$

(3)、 $(x^{4} + 2 x^{3} - \frac{1}{2} x^{2}) \div {(- \frac{1}{2} x)}^{2}$

查看试题解析
18. 先化简，再求值： ${(a - 1)}^{2} + 2 (a + 1) - 4$ ，其中 $a = \sqrt{3}$ ．

查看试题解析
19. 如图，点E、F在BC上，BE＝CF，AB＝DC，∠B＝∠C．求证：∠A＝∠D．

查看试题解析
20. 图①、图②、图③均是 $6 \times 6$ 的正方形网格，每个小正方形的顶点称为格点，点A、B、C、D、E、F均在格点上．只用无刻度的直尺按下列要求在给定的网格中画图，所画图形的顶点均在格点上，不要求写画法．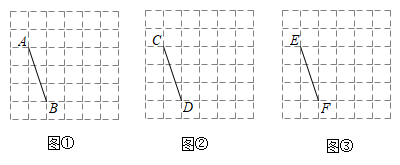

(1)、在图①中以线段 $A B$ 为一腰画一个等腰锐角三角形 $A B P$ ；

(2)、在图②中以线段CD为底画一个等腰直角三角形 $C D M$ ；

(3)、在图③中画等腰钝角三角形 $E F N$ ．

查看试题解析
21. 已知 $a + \frac{1}{a} = 3$ ，求：

(1)、 $a^{2} + \frac{1}{a^{2}}$ ；

(2)、 $a - \frac{1}{a}$ ．

查看试题解析
22. 如图，长为2，宽为a的矩形纸片（ $1 < a < 2$ ），剪去一个边长等于矩形宽度的正方形（称为第一次操作）；

(1)、第一次操作后剩下的矩形长为a，宽为；

(2)、再把第一次操作后剩下的矩形剪去一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去．
①求第二次操作后剩下的矩形的面积；

②若在第3次操作后，剩下的图形恰好是正方形，求 $a$ 的值．

查看试题解析
23. 教材呈现：如图是华师版八年级上册数学教材第96页的部分内容．

(1)、定理证明：请根据教材中的分析，结合图①，写出“角平分线的性质定理”完整的证明过程．

(2)、定理应用：
如图②， $△ A B C$ 的周长是12， $B O 、 C O$ 分别平分 $∠ A B C$ 和 $∠ A C B$ ， $O D ⊥ B C$ 于点D，若 $O D = 3$ ，则 $△ A B C$ 的面积为 ▲ ．

查看试题解析
24. 如图，在△ABC中，∠ACB＝90°，AC＝6，BC＝8.点P从点A出发，沿折线AC—CB以每秒1个单位长度的速度向终点B运动，点Q从点B出发沿折线BC—CA以每秒3个单位长度的速度向终点A运动，P、Q两点同时出发.分别过P、Q两点作PE⊥l于E，QF⊥l于F.设点P的运动时间为t（秒）：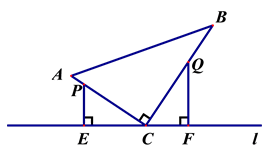

(1)、当P、Q两点相遇时，求t的值；

(2)、在整个运动过程中，求CP的长（用含t的代数式表示）；

(3)、当△PEC与△QFC全等时，直接写出所有满足条件的CQ的长.

查看试题解析