吉林省四平市双辽市2022-2023学年八年级上学期期中数学试题
试卷更新日期:2022-12-06 类型:期中考试
一、单选题
-
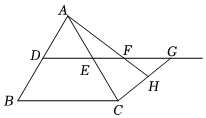
1. 已知三角形两边长分别为7、10,那么第三边的长可以是( )A、2 B、3 C、17 D、52. n 边形的每个外角都为 15°,则边数 n 为( )A、20 B、22 C、24 D、263. 如图,要测量湖两岸相对两点A,B的距离,可以在AB的垂线BF上取两点C,D,使CD=BC,再在BF的垂线DG上取点E,使点A,C,E在一条直线上,可得 . 判定全等的依据是( )
 A、 B、 C、 D、4. 已知,如图所示,AD=AC,BD=BC,O为AB上一点,那么,图中共有( )对全等三角形.
A、 B、 C、 D、4. 已知,如图所示,AD=AC,BD=BC,O为AB上一点,那么,图中共有( )对全等三角形. A、1 B、2 C、3 D、45. 如图, 中, , 是 中点,下列结论中错误的是( ).
A、1 B、2 C、3 D、45. 如图, 中, , 是 中点,下列结论中错误的是( ).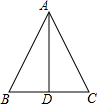 A、 B、 C、 平分 D、6. 和点P(﹣3,2)关于x轴对称的点是( )A、(3,2) B、(﹣3,2) C、(3,﹣2) D、(﹣3,﹣2)
A、 B、 C、 平分 D、6. 和点P(﹣3,2)关于x轴对称的点是( )A、(3,2) B、(﹣3,2) C、(3,﹣2) D、(﹣3,﹣2)二、填空题
-
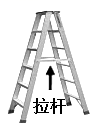
7. 人字梯中间一般会设计一”拉杆”,这样做的数学道理是 .
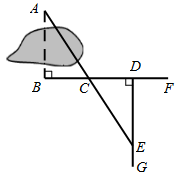
 8. 一个八边形的对角线共有条.9. 如图,在中, , 将△ABC沿着直线l折叠,使点B落在点F的位置,则的度数是 .
8. 一个八边形的对角线共有条.9. 如图,在中, , 将△ABC沿着直线l折叠,使点B落在点F的位置,则的度数是 .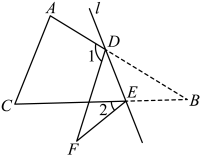 10. 如图,小虎用10块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( , ),点在上,点和分别与木墙的顶端重合,则两堵木墙之间的距离为 .
10. 如图,小虎用10块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( , ),点在上,点和分别与木墙的顶端重合,则两堵木墙之间的距离为 . 11. Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是 cm.12. 已知一个等腰三角形的一个内角为 ,则它的顶角等于 .13. 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E . 已知PE=3,则点P到AB的距离是
11. Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是 cm.12. 已知一个等腰三角形的一个内角为 ,则它的顶角等于 .13. 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E . 已知PE=3,则点P到AB的距离是 14. 如图,等腰 中, , 的垂直平分线 分别交 , 于点 , .若 ,则 .
14. 如图,等腰 中, , 的垂直平分线 分别交 , 于点 , .若 ,则 .
三、解答题
-
15. 如图,在△ABC中,AD⊥BC于D,AE平分∠DAC,∠BAC=80°,∠B=60°,求∠DAE的度数.
 16. 找出下列图形的所有的对称轴,并一一画出来.
16. 找出下列图形的所有的对称轴,并一一画出来. 17. 如图, , . 求证: .
17. 如图, , . 求证: . 18. 一个多边形的内角和比四边形的内角和多 , 并且这个多边形的各内角相等,求这个多边形是几边形?19. 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-1,1)、B(1,5)、C(4,4).
18. 一个多边形的内角和比四边形的内角和多 , 并且这个多边形的各内角相等,求这个多边形是几边形?19. 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-1,1)、B(1,5)、C(4,4). (1)、作出△ABC关于y轴对称的图形△A1B1C1 , 并写出顶点的坐标.(2)、求△A1B1C1的面积.20. 如图,已知AB=DC,AC=DB.求证:∠1=∠2.
(1)、作出△ABC关于y轴对称的图形△A1B1C1 , 并写出顶点的坐标.(2)、求△A1B1C1的面积.20. 如图,已知AB=DC,AC=DB.求证:∠1=∠2. 21. 如图,中, , 于E,F在上,且 , , 求证:是的平分线.
21. 如图,中, , 于E,F在上,且 , , 求证:是的平分线.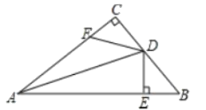 22. 如图,是线段的中点,平分 , 平分 , .
22. 如图,是线段的中点,平分 , 平分 , . (1)、求证:≌;(2)、若=50°,求的度数.23. 如图:已知等边中,D是AC的中点,E是BC延长线上的一点,且 , , 垂足为M.求证:
(1)、求证:≌;(2)、若=50°,求的度数.23. 如图:已知等边中,D是AC的中点,E是BC延长线上的一点,且 , , 垂足为M.求证: (1)、 ;(2)、M是BE的中点.
(1)、 ;(2)、M是BE的中点.