河北省唐山市路南区2022-2023学年八年级上学期11月期中考试数学试题

试卷更新日期：2022-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 观察下列图形，其中是三角形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 某三角形的三边长分别为3，6， $x$ ，则 $x$ 可能是（）

A、3 B、9 C、6 D、10

查看试题解析
3. 下列计算正确的是（）

A、 $a^{6} \div a^{2} = a^{4}$ B、 ${(a^{5})}^{2} = a^{7}$ C、 ${(a b^{2})}^{3} = a b^{6}$ D、 $a^{2} \cdot a^{3} = a^{6}$

查看试题解析
4. 一个多边形的内角和为 $α$ ，外角和为 $β$ ，则 $α = 2 β$ 的多边形的是（）

A、 B、 C、 D、

查看试题解析
5. 计算 ${(\underset{5 个 a^{2}}{\underset{︸}{a^{2} + a^{2} + ⋯ + a^{2}}})}^{3}$ 的结果是（）

A、 $125 a^{6}$ B、 $15 a^{5}$ C、 $a^{30}$ D、 $a^{13}$

查看试题解析
6. 已知 ${(x + 2)}^{2} = 0$ ，则 $x^{3}$ 的值等于（）

A、8 B、2 C、−3 D、−8

查看试题解析
7. 长方形的面积是3a²－3ab＋6a，一边长为3a，则它的另一条边长为（）

A、2a－b＋2 B、a－b＋2 C、3a－b＋2 D、4a－b＋2

查看试题解析
8. 如图，聪聪书上的三角形被墨迹污染了一部分，他根据所学知识很快画了一个与书本上完全一样的三角形，那么聪聪画图的依据是（）

A、SSS B、SAS C、ASA D、AAS

查看试题解析
9. 如图，OP平分∠AOB，点E为OA上一点，OE＝4，点P到OB的距离是2，则△POE的面积为（）

A、4 B、5 C、6 D、7

查看试题解析
10. 如图，四根木条钉成一个四边形框架 $A B C D$ ，要使框架稳固且不活动，至少还需要添加木条（）

A、1根 B、2根 C、3根 D、4根

查看试题解析
11. 下列各组图形中，BD是△ABC的高的图形是（）

A、 B、 C、 D、

查看试题解析
12. 如图，在△ABC中，∠A=90°，BE，CD分别平分∠ABC和∠ACB，且相交于F， $E G ∥ B C$ ， $C G ⊥ E G$ 于点G，则下列结论 ①∠CEG = 2∠DCA；②CA平分∠BCG；③∠ADC =∠GCD；④∠DFB= $\frac{1}{2}$ ∠A；⑤∠DFE=135°，其中正确的结论是（）

A、①②③ B、①③④ C、①③④⑤ D、①②③④

查看试题解析

二、填空题

13. 等腰三角形的两边分别为1和2，则其周长为．

查看试题解析
14. 如图，在△ABC中，D是BC延长线上一点，∠B=40°，∠ACD=120°，则∠A= ．

查看试题解析
15. 若 $m + n = 2 ， m^{2} - n^{2} = 12$ ，则 ${(m - n)}^{2} =$ ．

查看试题解析
16. 计算： $29 5^{2} + 10 \times 295 + 5^{2} =$

查看试题解析
17. 如图所示，直线a经过正方形ABCD的顶点A，分别过正方形的顶点B、D作BF⊥a于点F，DE⊥a于点E，若DE=8，BF=5，则EF的长为．

查看试题解析
18. 在平面直角坐标系中，点 $A (1 ， 0)$ ， $B (0 ， 2)$ ，作 $△ B O C$ ，使 $△ B O C$ 与 $△ A B O$ 全等（点 $C$ 与点 $A$ 不重合），则点 $C$ 坐标为．

查看试题解析

三、解答题

19.

(1)、 $m^{3} \cdot m \cdot {(m^{2})}^{3}$ ；

(2)、 $(9 a^{5} - 15 a^{3} + 6 a) \div (4 a - a)$ ．

查看试题解析
20. 在计算（x+a）（x+b）时，甲把b错看成了6，得到结果是：x²+8x+12．

(1)、求出a的值；

(2)、在（1）的条件下，且b＝-3时，计算（x+a）（x+b）的结果．

查看试题解析
21. 在△ABC中，BC＝8，AB＝1；

(1)、若AC是整数，求AC的长；

(2)、已知BD是△ABC的中线，若△ABD的周长为10，求△BCD的周长．

查看试题解析
22. 如图，学校劳动实践基地有两块边长分别为 $a$ ， $b$ 的正方形秧田 $A$ ， $B$ ，其中不能使用的面积为 $M$ ．

(1)、用含 $a$ ， $M$ 的代数式表示 $A$ 中能使用的面积；

(2)、若 $a + b = 10$ ， $a - b = 5$ ，求 $A$ 比 $B$ 多出的使用面积．

查看试题解析
23. 如图， $A B = A D ， B C = D C$ ，点 $E$ 在 $A C$ 上.

(1)、求证： $A C$ 平分 $∠ B A D$ ；

(2)、求证： $B E = D E$ .

查看试题解析
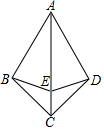24. 在一个三角形中，如果一个角是另一个角的3倍，这样的三角形我们称之为“智慧三角形”．如，三个内角分别为120°，40°，20°的三角形是“智慧三角形”．如图，∠MON=60°，在射线OM上找一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交射线OB于点C．

(1)、∠ABO的度数为°，△AOB（填“是”或“不是”） “智慧三角形”；

(2)、若∠OAC=20°，求证：△AOC为“智慧三角形”；

(3)、当△ABC为“智慧三角形”时，求∠OAC的度数．

查看试题解析
25. 问题背景：

(1)、如图1，在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B A D = 120 °$ ， $∠ B = ∠ A D C = 90 °$ ， $E$ ， $F$ 分别是 $B C$ ， $C D$ 上的点，且 $∠ E A F = 60 °$ ，探究图中线段 $B E$ 、 $E F$ 、 $F D$ 之间的数量关系，嘉琪同学探究此问题的方法是：延长 $F D$ 到点 $G$ ，使 $D G = B E$ ，连接 $A G$ ，先证明 $△ A B E ≌ △ A D G$ ，再证明 $△ A E F ≌ △ A G F$ ，可得出结论，他的结论应是．

(2)、探索延伸：①如图2，若在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B + ∠ D = 180 °$ ， $E$ 、 $F$ 分别是 $B C$ ， $C D$ 上的点，且 $∠ E A F = \frac{1}{2} ∠ B A D$ ，上述结论是否仍然成立，并说明理由．
②如图2，若五边形 $A B E F D$ 的面积为30， $B E = 4$ ， $D F = 6$ ，直接写出 $A$ 点到 $E F$ 的距离．

查看试题解析