北京市大兴区2022-2023学年八年级上学期期中数学试卷
试卷更新日期:2022-12-06 类型:期中考试
一、单选题
-
1. 在美术字中,有些汉字是轴对称的.下列美术字是轴对称的是( )A、爱 B、我 C、中 D、国2. 下列长度的三条线段,能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,3. 正五边形的内角和是( )A、 B、 C、 D、4. 如图图形中,作的边上的高,正确的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图, , 点 , , 在同一直线上,若 , , 则的度数是( )
5. 如图, , 点 , , 在同一直线上,若 , , 则的度数是( ) A、 B、 C、 D、6. 如图, , 若 , , 则的度数是( )
A、 B、 C、 D、6. 如图, , 若 , , 则的度数是( ) A、 B、 C、 D、7. 若从边形的一个顶点出发,可以画出条对角线,则的值是( )A、 B、 C、 D、8. 如图,在的正方形网格中,网格线的交点称为格点.已知 , 是两个格点,若点是图中的格点,且是等腰三角形,则点的个数是( )
A、 B、 C、 D、7. 若从边形的一个顶点出发,可以画出条对角线,则的值是( )A、 B、 C、 D、8. 如图,在的正方形网格中,网格线的交点称为格点.已知 , 是两个格点,若点是图中的格点,且是等腰三角形,则点的个数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 点P(2,3)关于x轴的对称点的坐标为 .10. 等腰三角形的一个内角为100°,则它的一个底角的度数为 .11. 如图,要测量池塘两岸相对的两点 , 的距离,作线段与相交于点若 , , , 则 , 两点间的距离为
 12. 已知如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足是D,写出图中的一组相似三角形 .
12. 已知如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足是D,写出图中的一组相似三角形 . 13. 如图,点 在同一条直线上,已知 ,若不增加任何字母和辅助线,要使 还需要添加的一个条件是.
13. 如图,点 在同一条直线上,已知 ,若不增加任何字母和辅助线,要使 还需要添加的一个条件是. 14. 如图,是等边三角形,是中点,于点 , 若 , 则的长是 .
14. 如图,是等边三角形,是中点,于点 , 若 , 则的长是 . 15. 将图中的折叠,使点与点重合,折痕为 , 点 , 分别在 , 上,得到图形若 , , 则的周长是 .
15. 将图中的折叠,使点与点重合,折痕为 , 点 , 分别在 , 上,得到图形若 , , 则的周长是 . 16. 如图,与都是等边三角形,和相交于点 , 连接下面结论中,;;不是的平分线;所有正确结论的序号是 .
16. 如图,与都是等边三角形,和相交于点 , 连接下面结论中,;;不是的平分线;所有正确结论的序号是 .
三、解答题
-
17. 用一条长的细绳围成一个等腰三角形,若一腰长是底边长的倍,求各边的长.18. 已知一个多边形的内角和是外角和的2倍,求这个多边形的边数.19. 如图,点A,B,C,D在同一直线上, , , . 求证: .
 20. 如图,线段与线段相交于点 , 若 , , , 求的度数.
20. 如图,线段与线段相交于点 , 若 , , , 求的度数.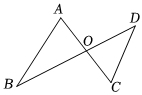 21. 如图,线段与线段相交于点 , , . 求证: .
21. 如图,线段与线段相交于点 , , . 求证: . 22. 如图, , 相交于点 , .
22. 如图, , 相交于点 , . (1)、作的角平分线 , 交于点(要求:尺规作图,保留作图痕迹,不写作法);(2)、若 , 则的形状是 .23. 如图,为了满足 , , 三个小区居民的体育锻炼需求,需要建立一个居民健身广场 , 要使健身广场到三个小区的距离相等,请你在图中作出健身广场的位置(要求:尺规作图,保留作图痕迹,不写作法).
(1)、作的角平分线 , 交于点(要求:尺规作图,保留作图痕迹,不写作法);(2)、若 , 则的形状是 .23. 如图,为了满足 , , 三个小区居民的体育锻炼需求,需要建立一个居民健身广场 , 要使健身广场到三个小区的距离相等,请你在图中作出健身广场的位置(要求:尺规作图,保留作图痕迹,不写作法). 24. 如图 , 是的中线.
24. 如图 , 是的中线.求证: .
请将下面的推理过程补充完整:
证明:如图 , 延长到点 , 使 , 连接 .
∵是的中线,
∴ .
在和中,
,
∴( ).
∴ ▲ (全等三角形的对应边相等).
∴在中,( ),
∴ .
即 .
 25. 如图,在中,是的中点, , , 垂足分别是点、 , . 求证:平分 .
25. 如图,在中,是的中点, , , 垂足分别是点、 , . 求证:平分 . 26. 在四边形中, , 平分 .
26. 在四边形中, , 平分 . (1)、如图 , 若 .
(1)、如图 , 若 .直接写出与的数量关系:;
请你写出图中一个与不同的正确结论:;
(2)、如图 , 若 , 猜想与的数量关系,并证明.27. 如图,在等边中,点是边上一点,作射线 , 点关于射线的对称点为 , 连接并延长交射线于点 . (1)、依题意补全图形;(2)、若 , 则的度数是;(3)、用等式表示线段 , , 之间的数量关系,并证明.28. 在平面直角坐标系中,点 , , 不在同一直线上,对于点和线段给出如下定义:过点向线段所在直线作垂线,若垂足在线段上,则称点为线段的内垂点,当垂足满足最小时,称点为线段的最佳内垂点.已知点 .
(1)、依题意补全图形;(2)、若 , 则的度数是;(3)、用等式表示线段 , , 之间的数量关系,并证明.28. 在平面直角坐标系中,点 , , 不在同一直线上,对于点和线段给出如下定义:过点向线段所在直线作垂线,若垂足在线段上,则称点为线段的内垂点,当垂足满足最小时,称点为线段的最佳内垂点.已知点 . (1)、在点中,线段的内垂点为;(2)、若点是线段的最佳内垂点,则点的坐标可以是(写出两个满足条件的点即可);(3)、已知点 , 若线段上的每一个点都是线段的内垂点,直接写出的取值范围;(4)、已知点 , , 若线段上存在线段的最佳内垂点,直接写出的取值范围.
(1)、在点中,线段的内垂点为;(2)、若点是线段的最佳内垂点,则点的坐标可以是(写出两个满足条件的点即可);(3)、已知点 , 若线段上的每一个点都是线段的内垂点,直接写出的取值范围;(4)、已知点 , , 若线段上存在线段的最佳内垂点,直接写出的取值范围.