安徽省安庆市怀宁县2022—2023学年八年级上学期期中数学试卷
试卷更新日期:2022-12-06 类型:期中考试
一、单选题
-
1. 在平面直角坐标系中,下列各点位于第四象限的点是( )A、 B、 C、 D、2. 下列式子中,表示y是x的正比例函数的是( )A、 B、 C、 D、3. 若点在一次函数的图象上,则点一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
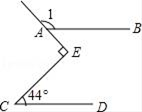 A、132° B、134° C、136° D、138°5. 周末小明和几个朋友到独秀山公园游玩,为测量独秀山公园前谷泉水库两对岸A、B两点之间的距离,小明在水库的一侧选取一点O,测得 , 则A、B间的距离可能是( )A、288m B、388m C、488m D、588m6. 已知 的三个内角的大小关系为 ,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定7. 如图,一次函数与一次函数的图象交于点P(1,3),则关于x的不等式的解集是( )
A、132° B、134° C、136° D、138°5. 周末小明和几个朋友到独秀山公园游玩,为测量独秀山公园前谷泉水库两对岸A、B两点之间的距离,小明在水库的一侧选取一点O,测得 , 则A、B间的距离可能是( )A、288m B、388m C、488m D、588m6. 已知 的三个内角的大小关系为 ,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定7. 如图,一次函数与一次函数的图象交于点P(1,3),则关于x的不等式的解集是( ) A、 B、 C、 D、8. 如图,在中,D为上一点, , 则的度数为( )
A、 B、 C、 D、8. 如图,在中,D为上一点, , 则的度数为( ) A、 B、 C、 D、9. 若一次函数的图象不经过第三象限,则( )A、 B、 C、 D、10. 甲、乙两人登山,登山过程中,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示.乙提速后,乙的登山速度是甲登山速度的3倍,并先到达山顶.根据图象所提供的信息,下列说法正确的有( )
A、 B、 C、 D、9. 若一次函数的图象不经过第三象限,则( )A、 B、 C、 D、10. 甲、乙两人登山,登山过程中,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示.乙提速后,乙的登山速度是甲登山速度的3倍,并先到达山顶.根据图象所提供的信息,下列说法正确的有( )①甲登山的速度是每分钟10米;②乙在A地时距地面的高度b为30米;③乙登山分钟时追上甲;④登山时间为4分钟、9分钟、13分钟时,甲、乙两人距地面的高度差为50米.
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在平面直角坐标系中,点不可能在第 象限.12. 已知点P、Q在一次函数的图象上,且 , 则m的取值范围是13. 如图,点E、F分别为、的中点,若的面积为32,则阴影部分的面积是
 14. 直线与直线分别交轴于 , 两点,两直线相交于轴上同一点 .(1)、(2)、若 , 点的坐标是
14. 直线与直线分别交轴于 , 两点,两直线相交于轴上同一点 .(1)、(2)、若 , 点的坐标是三、解答题
-
15. 一个等腰三角形的两条边长分别为5和10,求这个三角形的周长.16. 已知一次函数 的图象与y轴的负半轴相交,y随着x的增大而减小且m为整数,求m的值.17. 如图,在平面直角坐标系中,的顶点A、B、C的坐标分别为 , , 如果将先向右平移3个单位长度,再向下平移2个单位长度,会得到点、、分别为点A、B、C移动后的对应点.
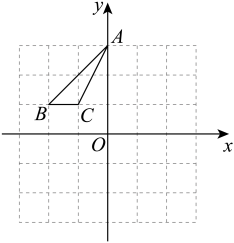 (1)、请直接写出点、、的坐标;(2)、请在图中画出三角形,并直接写出的面积.18. 如图,、分别是的高和角平分线, , , 求的大小.
(1)、请直接写出点、、的坐标;(2)、请在图中画出三角形,并直接写出的面积.18. 如图,、分别是的高和角平分线, , , 求的大小. 19. 在平面直角坐标系中,一条直线经过 , , 三点.求这条直线的解析式并求出a的值.20. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与x轴和y轴分别相交于点B和点E,与正比例函数的图象相交于点C,点C的横坐标为1.
19. 在平面直角坐标系中,一条直线经过 , , 三点.求这条直线的解析式并求出a的值.20. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与x轴和y轴分别相交于点B和点E,与正比例函数的图象相交于点C,点C的横坐标为1. (1)、求一次函数的解析式并直接写出点E的坐标;(2)、若点D在坐标轴上,且满足 ,求点D的坐标.
(1)、求一次函数的解析式并直接写出点E的坐标;(2)、若点D在坐标轴上,且满足 ,求点D的坐标.

