四川省自贡市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-12-06 类型：期末考试

进入出卷网下载

一、单选题

1. 抛物线 $y = - \frac{1}{2} x^{2} - 1$ 的开口方向是（）

A、向下 B、向上 C、向左 D、向右

查看试题解析
2. 如图，若 $⊙ O$ 的半径为5，圆心O到一条直线的距离为2，则这条直线可能是（）

A、 $l_{1}$ B、 $l_{2}$ C、 $l_{3}$ D、 $l_{4}$

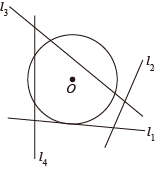查看试题解析
3. 用配方法解方程 $x^{2} + 8 x + 9 = 0$ ，配方后可得（）

A、 ${(x + 8)}^{2} = 73$ B、 ${(x + 4)}^{2} = 25$ C、 ${(x + 8)}^{2} = 55$ D、 ${(x + 4)}^{2} = 7$

查看试题解析
4. 学生甲手中有4，6，8三张扑克牌，学生乙手中有3，5，10三张扑克牌，现每人从各自手中随机取出一张牌进行比较，数字大者胜，在该游戏中（）

A、甲获胜的概率大 B、乙获胜的概率大 C、两人获胜概率一样大 D、不能确定

查看试题解析
5. 如图，将 $△ A B C$ 绕点A按逆时针方向旋转110°，得到 $△ A B^{'} C^{'}$ ，若点 $B^{'}$ 在线段BC的延长线上，则 $∠ B B^{'} C^{'}$ 的度数为（）

A、65° B、70° C、75° D、80°

查看试题解析
6. 如图，PA，PB是 $⊙ O$ 的切线，A，B是切点，点C是劣弧 $\overset{⌢}{A B}$ 上的一个点，若 $∠ A C B = 110 °$ ，则 $∠ P$ 的度数是（）

A、 $30^{°}$ B、 $40^{°}$ C、 $50^{°}$ D、 $70^{°}$

查看试题解析
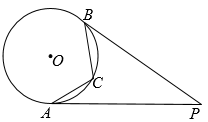7. 将一个正方形铁皮的四角各剪去一个边长为4cm的小正方形，做成的无盖盒子容积为 $400 {cm}^{3}$ ，则原铁皮的边长为（）

A、12cm B、14cm C、16cm D、18cm

查看试题解析
8. 如图，已知边长为2的正六边形ABCDEF内接于 $⊙ O$ ，则阴影部分的面积为（）

A、 $3 \sqrt{3}$ B、 $2 \sqrt{3}$ C、 $12 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
9. 若m、n是一元二次方程 $x^{2} + 2 x - 1 = 0$ 的两个实数根，则 $\frac{n^{3} + n^{2} m}{2 n - 1}$ 的值为（）

A、1 B、-1 C、2 D、-2

查看试题解析
10. 在利用正六面体骰子进行频率估计概率的试验中，小颖同学统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的试验可能是（）

A、朝上的点数是5的概率 B、朝上的点数是奇数的概率 C、朝上的点数大于2的概率 D、朝上的点数是3的倍数的概率

查看试题解析
11. 如图， $⊙ O$ 的半径为 $\sqrt{5}$ ， AB与CD为 $⊙ O$ 的两条平行弦， $∠ C D E = 30 °$ ， $A D = 2$ ，则弦BE的长为（）

A、3 B、3.5 C、 $5 \sqrt{2}$ D、 $2 + \sqrt{3}$

查看试题解析
12. 如图，二次函数 $y = a x^{2} + b x + c (a > 0)$ 的图象与x轴交于A，B两点，与y轴的正半轴交于点C，它的对称轴为直线 $x = - 1$ .有下列结论：① $a b c < 0$ ；② $4 a c - b^{2} < 0$ ；③ $c - a > 0$ ；④当 $x = - n^{2} - 2$ 时， $y \geq c$ ；⑤若 $x_{1}$ 、 $x_{2}$ （ $x_{1} < x_{2}$ ）是方程 $a x^{2} + b x + c = 0$ 的两根，则方程 $a (x - x_{1}) (x - x_{2}) - 1 = 0$ 的两根m、n（ $m < n$ ）满足 $m < x_{1}$ ，且 $n > x_{2}$ .其中，正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 如图，飞镖游戏板中每一块小正方形除颜色外都相同，把游戏板平放到露天地面上，请问落在该游戏板上的第一滴雨点正好打中阴影部分的概率是.

查看试题解析
14. 若关于x的一元二次方程 $x^{2} + 2 x + m - 1 = 0$ 有两个不相等的实数根，则实数m的取值范围是.

查看试题解析
15. 若点 $A (a ， 1)$ 与 $B (- 4 ， b)$ 关于原点成中心对称，则 $a^{b} =$ .

查看试题解析
16. 圆锥底面圆的半径为3，高为4，则圆锥侧面展开后的扇形圆心角是°.

查看试题解析
17. 如图，BD为边长为a的菱形ABCD的对角线， $∠ B A D = 60 °$ ，点M，N分别从点A，B同时出发.以相同的速度沿AB，BD向终点B和D运动，连接DM和AN，DM与AN相交于点P，连接BP，则BP的最小值为.

查看试题解析

三、解答题

18. 请阅读下列解题过程：
解一元二次不等式： $x^{2} - 3 x < 0$ .

解：设 $x^{2} - 3 x = 0$ ，解得 $x_{1} = 3$ ， $x_{2} = 0$ ，则抛物线 $y = x^{2} - 3 x$ 与x轴的交点坐标为 $(3 ， 0)$ 和 $(0 ， 0)$ ，画出 $y = x^{2} - 3 x$ 的大致图象：

由图像可知：当 $0 < x < 3$ 时，函数图象在x轴下方，此时 $y < 0$ 即 $x^{2} - 3 x < 0$ .所以一元二次不等式 $x^{2} - 3 x < 0$ 的解集为 $0 < x < 3$ .

通过上述解题过程的学习，按其解题思路和方法解答下列问题：

(1)、上述解题过程中，渗透了下列数学思想中的和（只填序号）
①分类讨论思想，②转化思想，③数形结合思想

(2)、用类似方法解 $x^{2} - 5 x + 6 > 0$ 的解集为.

查看试题解析
19. 解方程： $2 y (y + 2) - y = 2$ .

查看试题解析
20. 在校园文化艺术节中，九年级一班有1名男生和2名女生获得美术奖，另有2名男生和2名女生获得音乐奖.

(1)、从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会，刚好是男生的概率为；

(2)、分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会，用列表或树状图求刚好是一男生一女生的概率.

查看试题解析
21. 如图，在由边长为1的小正方形组成的网格中，△ABC的顶点均落在格点上．

(1)、将△ABC绕点O顺时针旋转90°后，得到△A₁B₁C₁ ．在网格中画出△A₁B₁C₁；

(2)、求线段OA在旋转过程中扫过的图形面积；(结果保留π)

查看试题解析
22. 如图，AB为 $⊙ O$ 的直径， $\overset{⌢}{B E} = \overset{⌢}{C E}$ ， $C D ⊥ A B$ 于D，交BE于F，连接CB.求证： $B C = C F$ .

查看试题解析
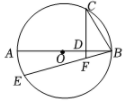23.
一幅长20cm、宽12cm的图案，如图，其中有一横两竖的彩条，横、竖彩条的宽度比为3：2．设竖彩条的宽度为xcm，图案中三条彩条所占面积为ycm² ．

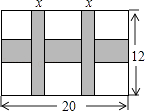(1)、求y与x之间的函数关系式；

(2)、若图案中三条彩条所占面积是图案面积的 $\frac{2}{5}$ ，求横、竖彩条的宽度．

查看试题解析
24. 如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．

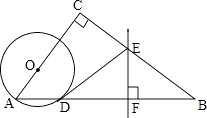(1)、判断直线DE与⊙O的位置关系，并说明理由；

(2)、若AC=6，BC=8，OA=2，求线段DE的长．

查看试题解析
25. 对于平面直角坐标系 $x O y$ 中的点P，给出如下定义：记点P到x轴的距离为 $d_{1}$ ，到y轴的距离为 $d_{2}$ ，若 $d_{1} \geq d_{2}$ ，则称 $d_{1}$ 为点P的最大距离；若 $d_{1} < d_{2}$ ，则称 $d_{2}$ 为点P的最大距离.例如：点 $P (- 3 ， 4)$ 到x轴的距离为4，到y轴的距离为3，因为 $3 < 4$ ，所以点P的最大距离为4.

(1)、①点 $A (2 ， - 5)$ 的最大距离为；
②若点 $B (a ， 2)$ 的最大距离为3，则a的值为；

③若点 $B (a ， 2)$ 的最大距离为2，则a的值为；

(2)、若点C在直线 $y = x - 2$ 上，且点C的最大距离为5，求点C的坐标；

(3)、若 $⊙ O$ 上存在点M，使点M的最大距离为 $5 \sqrt{2}$ ，直接写出 $⊙ O$ 的半径r的取值范围.

查看试题解析
26. 如图，把两个全等的 $R t △ A O B$ 和 $R t △ C O D$ 分别置于平面直角坐标系中，使直角边OB、OD在x轴上.已知点 $A (2 ， 4)$ ，过A、C两点的直线分别交x轴、y轴于点E、F，抛物线 $y = a x^{2} + b x + c$ 经过O、A、C三点.

(1)、求该抛物线的函数解析式；

(2)、点G为抛物线上位于线段OC所在直线上方部分的一动点，求G到直线OC的最大距离和此时点G的坐标；

(3)、点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM的边AM与边BP相等？若存在，求出此时点P的坐标；若不存在，请说明理由.

查看试题解析