四川省乐山市峨眉山市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-12-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）.

A、 $2 x + 3 = 0$ B、 $2 x - y = 0$ C、 $a x^{2} + b x + c = 0$ D、 $2 x^{2} + 3 x - 1 = 0$

查看试题解析
2. 二次根式 $\sqrt{x + 3}$ 有意义，x的取值范围是（）.

A、x≥－3 B、x＞－3 C、x≥0 D、x≥3

查看试题解析
3. 下列事件中，是必然事件的是（）.

A、一名运动员跳高的最好成绩是20.1米 B、通常加热到100℃时，水沸腾 C、一人买一张火车票，座位刚好靠窗口 D、购买一张彩票，中奖

查看试题解析
4. 用公式法解方程 $x^{2} + x = 2$ 时，求根公式中a，b，c的值分别是（）.

A、 $a = 1$ ， $b = 1$ ， $c = 2$ B、 $a = 1$ ， $b = - 1$ ， $c = - 2$ C、 $a = 1$ ， $b = 1$ ， $c = - 2$ D、 $a = 1$ ， $b = - 1$ ， $c = 2$

查看试题解析
5. 若 $\frac{2}{a} = \frac{3}{b} = \frac{4}{c}$ ，则 $\frac{3 a + 2 b + c}{2 a - 3 b - c}$ 的值是（）

A、 $\frac{16}{9}$ B、 $- \frac{16}{9}$ C、 $- 16$ D、 $- \frac{1}{9}$

查看试题解析
6. 如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为2：5，且三角板的一边长为8cm，则投影三角板的对应边长为（）

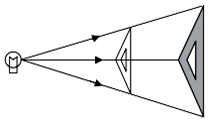A、20cm B、10cm C、8cm D、3.2cm

查看试题解析
7. 某市从2018年开始大力发展旅游产业．据统计，该市2018年旅游收入约为2亿元．预计2020年旅游收入约达到2.88亿元，设该市旅游收入的年平均增长率为x，下面所列方程正确的是（）

A、2（1+x）²＝2.88 B、2x²＝2.88 C、2（1+x%）²＝2.88 D、2（1+x）+2（1+x）²＝2.88

查看试题解析
8. 若 $5 k + 20 < 0$ ，则关于x的一元二次方程 $x^{2} + 4 x - k = 0$ 的根的情况是（）

A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断

查看试题解析
9. 如图，已知 $D E ∥ B C$ ， $E F // A B$ ，则下列比例式中错误的是（）.

A、 $\frac{C G}{D G} = \frac{C F}{B F}$ B、 $\frac{E G}{F G} = \frac{A D}{B D}$ C、 $\frac{D E}{B C} = \frac{A D}{B D}$ D、 $\frac{E F}{A B} = \frac{C G}{C D}$

查看试题解析
10. 如图，在 $A$ 处测得点 $P$ 在北偏东 $60 °$ 方向上，在 $B$ 处测得点 $P$ 在北偏东 $30 °$ 方向上，若 $A P = 6 \sqrt{3}$ 千米，则点 $A B$ 两点的距离为（）千米．

A、4 B、 $4 \sqrt{3}$ C、2 D、6

查看试题解析
11. 公元三世纪，我国汉代数学家赵爽在注解 $《$ 周髀算经 $》$ 时给出的“赵爽弦图”如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125，小正方形面积是25，则 ${(s i n θ - c o s θ)}^{2} = （）$

A、 $\frac{1}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{3 \sqrt{5}}{5}$ D、 $\frac{9}{5}$

查看试题解析
12. 若方程 $x^{2} - 2 x - 1 = 0$ 的根也是方程 $x^{3} + a x^{2} + b x + c = 0$ 的根，则 $3 a + b + c$ 的值为（）.

A、7 B、 $- 7$ C、5 D、 $- 5$

查看试题解析

二、填空题

13. 计算： $\sqrt{16}$ = ．

查看试题解析
14. 比较大小： $2 \sqrt{3}$ 17（填“>”、“<”、“=”）.

查看试题解析
15. 把一元二次方程 $x (3 x + 2) = x - 2$ 化成一般形式是.

查看试题解析
16. 方程x²﹣2x=0的解为．

查看试题解析
17.
如图，A、B、C三点在正方形网格线的交点处．若将△ACB绕着点A逆时针旋转得到△AC′B′，则tanB′的值为

查看试题解析
18. 如图，从一个大正方形中裁去面积为 $30 {cm}^{2}$ 和 $48 {cm}^{2}$ 的两个正方形，则余下阴影部分的面积为 ${cm}^{2}$ .

查看试题解析
19. 已知 $y = \sqrt{x - 1} + \sqrt{5 - x}$ （x，y均为实数），则y的最大值是.

查看试题解析
20. 如图，△ABC，△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，将△ADE绕点A在平面内自由旋转，连接DC，点M，P，N分别为DE，DC，BC的中点，若AD=3，AB=7，则线段MN的取值范围是．

查看试题解析

三、解答题

21. $(\sqrt{12} + 5 \sqrt{8}) \cdot \sqrt{3}$ .

查看试题解析
22. 解方程： $x (3 x - 1) = 3 - x$ .

查看试题解析
23. 计算： $- \sqrt{27} \div \sqrt{3} - \sqrt{12} + 6 \sin 30 °$ .

查看试题解析
24. 若最简二次根式 $\sqrt[3 x - 10]{2 x + y - 5}$ 和 $\sqrt{x - 3 y + 11}$ 是同类二次根式，求 $x + y$ 的值.

查看试题解析
25. 如图，在△ABC中，D、E分别是边AB、AC的中点，F为CA延长线上一点，∠F=∠C.

(1)、若BC=8，求FD的长；

(2)、若AB=AC，求证：△ADE∽△DFE.

查看试题解析
26. 某中学举行钢笔书法大赛，对各年级同学的获奖情况进行了统计，并绘制了如下两幅不完整的统计图.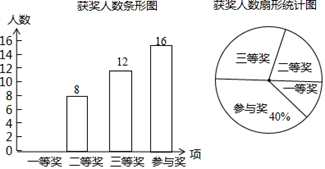

请结合图中相关信息解答下列问题：

(1)、扇形统计图中三等奖所在扇形的圆心角的度数是度；

(2)、请将条形统计图补全；

(3)、获得一等奖的同学中有 $\frac{1}{4}$ 来自七年级，有 $\frac{1}{4}$ 来自九年级，其他同学均来自八年级.现准备从获得一等奖的同学中任选2人参加市级钢笔书法大赛，请通过列表或画树状图的方法求所选出的2人中既有八年级同学又有九年级同学的概率.

查看试题解析
27. 已知关于x的一元二次方程 $x^{2} - 6 x + 2 m - 1 = 0$ 有 $x_{1}$ ， $x_{2}$ 两实数根.

(1)、若 $x_{1} = 1$ ，求 $x_{2}$ 及 $m$ 的值；

(2)、是否存在实数 $m$ ，满足 $(x_{1} - 1) (x_{2} - 1) = \frac{6}{m - 5}$ ？若存在，求出求实数 $m$ 的值；若不存在，请说明理由.

查看试题解析

28. 研究函数性质时，我们经历了列表、描点、连线画出函数图象，观察分析函数特征，概括函数性质的过程，已知函数

y = | \frac{6}{| x - 1 |} - 3 |

，结合已有的学习经验，完成下列各小题.

(1)、请在下列表格空白处填入恰当的数据；

x	…	-5	-1	0	0.5	1.5			4	7	…
y	…	2	0	3	9		3		1	2	…

(2)、根据上表中的数据，在所给的平面直角坐标系中补全函数

y = | \frac{6}{| x - 1 |} - 3 |

的图象；

(3)、根据你所画的该函数图象，该函数图象的对称轴是：；

(4)、结合你所画的函数图象，直接写出方程

| \frac{6}{| x - 1 |} - 3 | = \frac{1}{3} x + 4

的近似解为：.（结果保留一位小数，误差不超过0.2）

查看试题解析

29. 如图，点E，F分别在矩形ABCD的边AB，BC上，连接EF，将△BEF沿直线EF翻折得到△HEF，AB＝8，BC＝6，AE：EB＝3：1.

(1)、如图1，当∠BEF＝45°时，EH的延长线交DC于点M，求HM的长；

(2)、如图2，当FH的延长线经过点D时，求tan∠FEH的值；

(3)、如图3，连接AH，HC，当点F在线段BC上运动时，试探究四边形AHCD的面积是否存在最小值？若存在，求出四边形AHCD的面积的最小值；若不存在，请说明理由.

查看试题解析
30. 如图，在Rt $△$ ABC中，AC＝BC ， ∠ACB＝90°，点O在线段AB上（点O不与点A ， B重合），且OB＝kOA ，点M是AC延长线上的一点，作射线OM ，将射线OM绕点O逆时针旋转90°，交射线CB于点N ．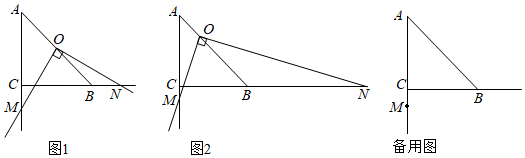

(1)、如图1，当k＝1时，判断线段OM与ON的数量关系，并说明理由；

(2)、如图2，当k＞1时，判断线段OM与ON的数量关系（用含k的式子表示），并证明；

(3)、点P在射线BC上，若∠BON＝15°，PN＝kAM（k≠1），且 $\frac{C M}{A C}$ ＜ $\frac{\sqrt{3} - 1}{2}$ ，请直接写出 $\frac{N C}{P C}$ 的值（用含k的式子表示）．

查看试题解析