吉林省长春市长春汽车经济技术开发区2022-2023学年七年级上学期期中数学试题

试卷更新日期：2022-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 2022的相反数是（）

A、 $\frac{1}{2022}$ B、 $- \frac{1}{2022}$ C、2022 D、-2022

查看试题解析
2. 冬天的脚步近了，白天和夜晚的温差很大，白天的最高气温能达到10 $℃$ 左右，夜晚的最低气温为-1 $℃$ 左右，则白天最高气温与夜晚最低气温的温差是（）

A、-9 $℃$ B、-11 $℃$ C、9 $℃$ D、11 $℃$

查看试题解析
3. 长春轨道客车股份有限公司制造的新型奥运版复兴号智能动车组，车头采用鹰隼形的设计，能让性能大幅提升，一列该动车组一年运行下来可节省约1800000度电，将数据1800000用科学记数法表示为（）

A、 $18 \times 1 0^{5}$ B、 $1.8 \times 1 0^{6}$ C、 $1.8 \times 1 0^{7}$ D、 $0.18 \times 1 0^{7}$

查看试题解析
4. 实数a，b在数轴上对应点的位置如图所示，下列结论正确的是（）

A、 $a > 0$ B、 $a < b$ C、 $a + b < 0$ D、 $a b > 0$

查看试题解析
5. 下列各数：0， $| - 2 |$ ，-（-2），-3² ， $\frac{1}{- 2^{2}}$ ，其中非负数有（）个．

A、1 B、2 C、3 D、4

查看试题解析
6. 下列各单项式中，与 $- 2 m n^{2}$ 是同类项的是（）

A、 $5 m n$ B、 $2 n^{2}$ C、 $3 m^{2} n$ D、 $m n^{2}$

查看试题解析
7. 下列说法正确的是（）

A、4a³b的次数是3 B、多项式x²−1是二次三项式 C、2a+b−1的各项分别为2a，b，1 D、−3ab²的系数是−3

查看试题解析
8. 为庆祝国庆，小明用大小相等的五角星按一定规律摆出如下图案，则第15个图案五角星的颗数为（）

A、46 B、49 C、52 D、55

查看试题解析

二、填空题

9. 比较大小：-5-7（填 $>$ 或＝或 $<$ 号）

查看试题解析
10. 用四舍五入法取近似数： $3.2652 \approx$ （精确到百分位）．

查看试题解析
11. 将多项式x²－1＋2x－3x³按x的降幂排列.

查看试题解析
12. 香蕉的单价为a元/千克，苹果的单价为b元/千克，买2千克苹果和3千克香蕉共需元．

查看试题解析
13. 若3a^mb⁵与4a²bⁿ⁺¹是同类项，则m+n＝.

查看试题解析
14. 若 $2 a - 3 b = 2$ ，则多项式 $4 a - 6 b - 5$ 的值是．

查看试题解析

三、解答题

15. 在数轴上表示下列各数，并按照从小到大的顺序用“ $<$ ”号连接起来．
$| - 3 |$ ， $- \frac{5}{2}$ ， 0， $- (- 1.5)$ ， -2．

查看试题解析
16. 计算：

(1)、 $- 20 + 18 - (- 12) + 10$ ；

(2)、 $3 \times (- 4) + 18 \div (- 6) - (- 5)$ ；

(3)、 ${(- 2)}^{3} + 9 \times {(- \frac{2}{3})}^{2} \div (- \frac{1}{2})$ ；

(4)、 $- 1^{2} - \frac{1}{4} \times [5 - {(- 3)}^{2}]$ ；

(5)、 $39 \frac{23}{24} \times (- 12)$ ；

(6)、 $(\frac{1}{2} + \frac{5}{6} - \frac{7}{12}) \times (- 24)$ ．

查看试题解析
17. 化简求值 $5 a b - 7 a^{2} b^{2} - 8 a b + 7 a^{2} b^{2} - a b + 5$ ，其中 $a = - 2 ， b = - \frac{1}{2}$ ．

查看试题解析
18. 为了提高业主的宜居环境，在某居民区的建设中，因地制宜规划修建一个广场（图中阴影部分）（单位米）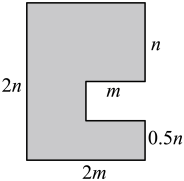

(1)、用含 $m$ 、 $n$ 的代数式表示该广场的周长

(2)、当 $m = 6$ ， $n = 8$ 时，求出该广场的周长．

查看试题解析
19. 已知关于x的多项式 $m x^{3} - 2 x^{2} + 3 x - 4 x^{3} + 5 x^{2} - n x$ 不含三次项和一次项，求 ${(n - m)}^{m n}$ 的值.

查看试题解析
20. 如今，网上购物已成为一种新的消费时尚，晶晶文具店想购买一种贺年卡在元旦时销售，在互联网上搜索了甲、乙两家网店（如图所示），已知两家网店的这种贺年卡完全相同，根据图回答下列问题：

(1)、若晶晶文具店想购买x张贺年卡，
当 $x \leq 30$ 时，在甲网店需要花费元，在乙网店需要花费元；
当 $x > 30$ 时，在甲网店需要花费元，在乙网店需要花费元；
（提示：以上费用均用含x的式子表示，如需付运费时，运费只需付一次，即10元）

(2)、晶晶文具店打算购买200张贺年卡，选择哪家网店更省钱？

查看试题解析

21. 2020年的“新冠肺炎”疫情的蔓延，使得医用口罩销量大幅增加，某口罩加工厂为满足市场需求计划每天生产5000个，由于各种原因实际每天生产量相比有出入，下表是二月份某一周的生产情况（超产为正，减产为负，单位：个）．

星期	一	二	三	四	五	六	日
增减	+100	-200	+400	100	-100	+350	+150

(1)、根据记录可知前三天共生产多少个口罩；

(2)、产量最多的一天比产量最少的一天多生产多少个；

(3)、该口罩加工厂实行计件工资制，每生产一个口罩0.2元，本周口罩加工厂应支付工人的工资总额是多少元？

查看试题解析

22. 小明是个聪明而富有想象力的孩子，学习了“有理数的乘方”后，他就琢磨着使用乘方这一数学知识，脑洞大开地定义出“有理数的除方”概念．于是规定：求若干个相同的不为零的有理数的除法运算叫做除方，如： $2 \div 2 \div 2$ ， $(- 3) \div (- 3) \div (- 3) \div (- 3)$ 等，类比有理数的乘方，我们把 $2 \div 2 \div 2$ 记作 $2^{③}$ ，读作“2的圈3次方”： $(- 3) \div (- 3) \div (- 3) \div (- 3)$ 记做 $（ - 3 ）^{④}$ ，读作“-3的圈4次方”，一般地，把 $\underset{n 个 a}{\underset{︸}{a \div a \div a \div \dots \div a}}$ （ $a \neq 0$ ）记做 $a^{ⓝ}$ 读作“a的圈n次方”．

(1)、直接写出计算结果
${(- \frac{1}{2})}^{③} =$ ； $（ - 3 ）^{④} =$ ； $2^{⑤} =$ ；

(2)、小明深入思考后发现，有理数的“除方”运算能转化为乘方运算，且结果可以写成幂的形式，推导出“除方”的运算公式归纳如下： $a^{ⓝ} =$ （n为正整数且 $a \neq 0$ ， $n \geq 2$ ）（要求将结果写成幂的形式，结果用含a，n的式子表示）；

(3)、请利用（2）问的推导公式计算 $24 \div 2^{3} + (- 8) \times 2^{③}$ ．

查看试题解析
23. 已知在数轴上点M、N表示的数分别为a，b，点M、N两点之间的距离表示为 $| a - b |$ 或 $| b - a |$ ，记为 $| M N | = | a - b | = | b - a |$ ．如图，已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．点P是数轴上任意一点，

(1)、数轴上点B表示的数是；

(2)、如果点P到点A、点B的距离相等，那么点P表示的数是；

(3)、若点P到点A、点B的距离之和等于14，则点P表示的数为；

(4)、若点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动．动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，运动时间为t．求：
①当 $t = 1$ 秒时P，Q两点间的距离为 ▲ ；

②当点P运动多少秒时，点P与点Q相遇？

③当点P与点Q间的距离为8个单位长度时t的值为 ▲ ．

查看试题解析