四川省广安市岳池县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-12-06 类型:期末考试
一、单选题
-
1. 下列图形中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若关于的方程是一元二次方程,则的取值范围是( )A、 B、 C、 D、3. 下列事件中,是必然事件的是( )A、抛掷一枚硬币,反面朝上 B、打开电视,正在播放《美术经典中的党史》 C、任意画一个四边形,它的内角和等于 D、在一个只装有白球的口袋中摸出红球4. 如图,四边形内接于 , , 则的度数是( )
2. 若关于的方程是一元二次方程,则的取值范围是( )A、 B、 C、 D、3. 下列事件中,是必然事件的是( )A、抛掷一枚硬币,反面朝上 B、打开电视,正在播放《美术经典中的党史》 C、任意画一个四边形,它的内角和等于 D、在一个只装有白球的口袋中摸出红球4. 如图,四边形内接于 , , 则的度数是( )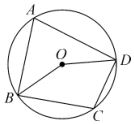 A、 B、 C、 D、5. 一个不透明的箱子中有2个白球、3个黄球和4个红球,这些球除颜色不同外无其他差别.从箱子中随机摸出1个球,它是红球的概率是( )A、 B、1 C、 D、6. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定7. 把抛物线向右平移3个单位长度,再向下平移5个单位长度,得到的抛物线是( )A、 B、 C、 D、8. 我县某村从2018年开始大力发展文旅产业,打造农家生态文化旅游.据统计,该村2018年农家生态文化旅游收入约为200万元,2020年该村农家生态文化旅游收入达到288万元.据此估计该村从2018年到2020年农家生态文化旅游收入的年平均增长率为( )A、 B、 C、 D、9. 如图,的直径弦于点 , 连接.若 , , 则的长为( )
A、 B、 C、 D、5. 一个不透明的箱子中有2个白球、3个黄球和4个红球,这些球除颜色不同外无其他差别.从箱子中随机摸出1个球,它是红球的概率是( )A、 B、1 C、 D、6. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定7. 把抛物线向右平移3个单位长度,再向下平移5个单位长度,得到的抛物线是( )A、 B、 C、 D、8. 我县某村从2018年开始大力发展文旅产业,打造农家生态文化旅游.据统计,该村2018年农家生态文化旅游收入约为200万元,2020年该村农家生态文化旅游收入达到288万元.据此估计该村从2018年到2020年农家生态文化旅游收入的年平均增长率为( )A、 B、 C、 D、9. 如图,的直径弦于点 , 连接.若 , , 则的长为( ) A、 B、 C、 D、10. 二次函数的图象如图所示,有以下四个结论:①;②;③1和-3是关于的一元二次方程的两个实数根;④对于任意实数 , 都有.其中正确结论的个数是( )
A、 B、 C、 D、10. 二次函数的图象如图所示,有以下四个结论:①;②;③1和-3是关于的一元二次方程的两个实数根;④对于任意实数 , 都有.其中正确结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 已知是关于的一元二次方程的一个实数根,则.12. 小麦是中国重要的粮食作物之一,传入中国的时间较早据考古发掘新疆孔雀河流域新石器时代遗址出土的炭化小麦,距今400年以上.今年某乡村振兴实验室,从某小麦新品种的种子中抽取6批,在相同条件下进行发芽实验,数据统计如表:
种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
95
358
744
893
1804
4505
发芽频率
0.950
0.895
0.930
0.893
0.902
0.901
据此可知,该种子发芽的概率为(精确到0.1).
13. 若点关于原点对称的点是 , 则.14. 如图,⊙O与正五边形ABCDE的两边AE、CD分别相切于A、C两点,则∠AOC的度数为度.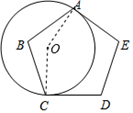 15. 赵州桥的桥拱横截面是近似的抛物线形,其示意图如图所示,其解析式为y=-x2.当水面离桥拱顶的高度DO为4m时,水面宽度AB为m.
15. 赵州桥的桥拱横截面是近似的抛物线形,其示意图如图所示,其解析式为y=-x2.当水面离桥拱顶的高度DO为4m时,水面宽度AB为m. 16. 如图,已知等边三角形绕点顺时针旋转得到 , , 分别为线段和线段上的动点,且 , 有以下结论:①四边形为菱形;②;③为等边三角形;④.其中正确结论有.(填序号)
16. 如图,已知等边三角形绕点顺时针旋转得到 , , 分别为线段和线段上的动点,且 , 有以下结论:①四边形为菱形;②;③为等边三角形;④.其中正确结论有.(填序号)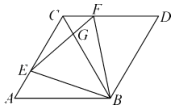
三、解答题
-
17. 用配方法解方程:.18. 如图,在平面直角坐标系中,三个顶点的坐标分别为 , , .
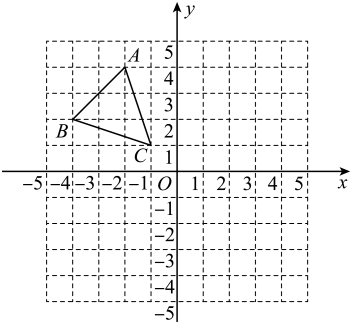 (1)、画出关于原点对称的;(2)、求的面积.19. 关于的一元二次方程有实数根.(1)、求的取值范围;(2)、若方程的两个实数根为 , , 且满足 , 求的值.20. 如图,为的直径,为上一点,为的中点,交直线于点.
(1)、画出关于原点对称的;(2)、求的面积.19. 关于的一元二次方程有实数根.(1)、求的取值范围;(2)、若方程的两个实数根为 , , 且满足 , 求的值.20. 如图,为的直径,为上一点,为的中点,交直线于点. (1)、求证:;(2)、若 , , 求的直径.21. 岳池县是电子商务百强县,某商店积极利用网络优势销售当地特产—西板豆豉.已知每瓶西板豆豉的成本价为16元,当销售单价定为20元时,每天可售出80瓶.为了回馈广大顾客,该商店现决定降价销售(销售单价不低于成本价).经市场调查反映:若销售单价每降低0.5元,则每天可多售出20瓶.(1)、当销售单价降低1元时,每天的销售利润为元;(2)、为尽可能让利于顾客,若该商店销售西板豆豉每天的实际利润为350元,求西板豆豉的销售单价.22. 某地区为了了解2022年初中毕业生毕业去向的意向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四类意向:. 读普通高中;. 读职业高中;. 直接进入社会就业;. 其他(如出国等)进行数据统计,并绘制了如下两幅不完整的统计图.
(1)、求证:;(2)、若 , , 求的直径.21. 岳池县是电子商务百强县,某商店积极利用网络优势销售当地特产—西板豆豉.已知每瓶西板豆豉的成本价为16元,当销售单价定为20元时,每天可售出80瓶.为了回馈广大顾客,该商店现决定降价销售(销售单价不低于成本价).经市场调查反映:若销售单价每降低0.5元,则每天可多售出20瓶.(1)、当销售单价降低1元时,每天的销售利润为元;(2)、为尽可能让利于顾客,若该商店销售西板豆豉每天的实际利润为350元,求西板豆豉的销售单价.22. 某地区为了了解2022年初中毕业生毕业去向的意向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四类意向:. 读普通高中;. 读职业高中;. 直接进入社会就业;. 其他(如出国等)进行数据统计,并绘制了如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)、该地区共调查了名九年级学生;(2)、将条形统计图补充完整;(3)、老师想从甲、乙、丙、丁4位同学中随机选择两位同学了解他们毕业去向的意向情况,请用画树状图或列表的方法求出恰好选中甲、丙两位同学的概率.23. 网络直播销售已经成为一种热门的销售方式,某公司在一销售平台上进行直播销售直条米粉.已知直条米粉的成本价为4元/kg,每日销售量y(单位:kg)与销售单价x(单位:元/kg)满足一次函数关系,如表记录的是有关数据.经销售发现,直条米粉的销售单价不低于成本价且不高于15元.销售单价/(元/)
5
6
7
每日销售量
150
140
130
(1)、求日销售量与销售单价之间的函数关系式;(2)、设该公司销售直条米粉的日利润为元.当销售单价定为多少元时,销售这种直条米粉的日利润最大?最大是多少?24. 如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针方向旋转一定的角度,得到△ADC,连接OD,OA. (1)、求∠ODC的度数;(2)、试判断AD与OD的位置关系,并说明理由;(3)、若OB=2,OC=3,求AO的长(直接写出结果).
(1)、求∠ODC的度数;(2)、试判断AD与OD的位置关系,并说明理由;(3)、若OB=2,OC=3,求AO的长(直接写出结果).

