广东省梅州市五华县2022-2023学年七年级上学期期中统考数学试题
试卷更新日期:2022-12-06 类型:期中考试
一、单选题
-
1. 下列各数中,最小的数是( )A、 B、-2 C、 D、02. 今年9月19日,我国自主设计研制的第三代航天远洋测量船远望5号圆满完成两次海上测控任务后,已安全顺利返回中国卫星海上测控母港.本次出航,远望5号历时69天,安全航行14000余海里.其中,数字14000用科学记数法表示为( )A、 B、 C、 D、3. -2022的倒数是( )A、2022 B、-2022 C、 D、4. 下列各图经过折叠后不能围成一个正方体的是( )A、
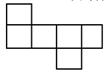 B、
B、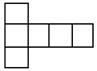 C、
C、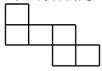 D、
D、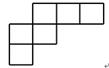 5. 定义一种运算: , 例如 , 则( )A、10 B、-10 C、-8 D、126. 用一个平面截一个正方体,截面形状不可能是( )A、三角形 B、四边形 C、五边形 D、七边形7. 下列说法正确的是( )A、单项式的系数是 B、单项式的次数是4 C、多项式是二次三项式 D、多项式的项分别是、2x、38. 如图,将一刻度尺放在数轴上,(数轴的单位长度是),刻度尺上对应数轴上的数3,那么数轴上-2.5对应刻度尺上的数字为:( )
5. 定义一种运算: , 例如 , 则( )A、10 B、-10 C、-8 D、126. 用一个平面截一个正方体,截面形状不可能是( )A、三角形 B、四边形 C、五边形 D、七边形7. 下列说法正确的是( )A、单项式的系数是 B、单项式的次数是4 C、多项式是二次三项式 D、多项式的项分别是、2x、38. 如图,将一刻度尺放在数轴上,(数轴的单位长度是),刻度尺上对应数轴上的数3,那么数轴上-2.5对应刻度尺上的数字为:( )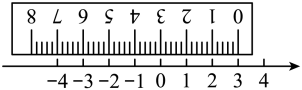 A、5.3 B、5.5 C、-5.5 D、69. 某一长方体纸盒的表面展开图如图所示,根据图中数据可得该长方体纸盒的容积为:( )
A、5.3 B、5.5 C、-5.5 D、69. 某一长方体纸盒的表面展开图如图所示,根据图中数据可得该长方体纸盒的容积为:( )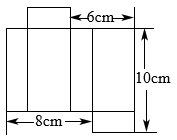 A、 B、 C、 D、10. 按《航空障碍灯(MH/T6012-2015)》的要求,为保障飞行器夜间飞行的安全,在高度为45米至105米的建筑上必须安装中光强航空障碍灯(AviationObstructionlight),中光强航空障碍灯闪光频率不低于每分钟20次,不高于每分钟70次,下图是某一种中光强航空障碍灯的闪光模式,灯的亮暗呈规律性交替变化,那么在一个连续的10秒内,该航空障碍灯处于亮的状态时间总和最长可达:( )
A、 B、 C、 D、10. 按《航空障碍灯(MH/T6012-2015)》的要求,为保障飞行器夜间飞行的安全,在高度为45米至105米的建筑上必须安装中光强航空障碍灯(AviationObstructionlight),中光强航空障碍灯闪光频率不低于每分钟20次,不高于每分钟70次,下图是某一种中光强航空障碍灯的闪光模式,灯的亮暗呈规律性交替变化,那么在一个连续的10秒内,该航空障碍灯处于亮的状态时间总和最长可达:( ) A、6.5秒 B、7秒 C、7.5秒 D、13秒
A、6.5秒 B、7秒 C、7.5秒 D、13秒二、填空题
-
11. 等高线指的是地形图上海拔相等的相邻各点所连成的闭合曲线,在等高线上标注的数字为该等高线的海拔.若高于海平面10米记为+10米,某地的高度低于海平面25米,则此处的等高线标注为米.12. 若x,y为有理数,且 , 则的值为 .13. 若 , 则的值是 .14. 已知,如下图,某长方形广场的四角都有一块边长为x米的正方形草地,若长方形的长为a米,宽为b米,则阴影部分的面积可表示为平方米.
 15. 一个几何体,它从正面和上面看到的形状图如图所示,则这个几何体最少有个小立方块.
15. 一个几何体,它从正面和上面看到的形状图如图所示,则这个几何体最少有个小立方块.
三、解答题
-
16. 计算: .17. 已知a,b互为相反数,c,d互为倒数,且 , 求的值.18. 已知一个由几个小正方体搭成的几何体,从上面看这个几何体的形状如图所示,小正方形中的数字表示在该位置上小正方体的个数,请画出从正面和左面看到的这个几何体的形状图.
 19. 有人说:美食是城市的信仰,夜市是城市的灵魂.今年国庆黄金周期间,小王用2000元购买了一批珍珠奶茶原料,在网红夜市中农批市场摆地摊售卖7天,全部销售完毕.每天的收入以300元为标准,超过的钱数记作正数,不足的钱数记作负数,7天的收入记录如下: . (单位:元)(1)、收入最多的一天比最少的一天多多少元?(2)、小王这7天的地摊收入是盈利还是亏损?盈利或亏损多少元?20. 已知 , .(1)、化简 ,(2)、当与是同类项时,求的值.21. 某班计划买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价100元,乒乓球每盒定价20元.经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠,该班需球拍5副,乒乓球若干盒(不少于5盒).(1)、若该班需购买乒乓球x盒,用含x的式子分别表示在甲、乙两家商店购买的费用.(2)、当分别购买20盒、30盒乒乓球时,去哪家商店购买更合算?
19. 有人说:美食是城市的信仰,夜市是城市的灵魂.今年国庆黄金周期间,小王用2000元购买了一批珍珠奶茶原料,在网红夜市中农批市场摆地摊售卖7天,全部销售完毕.每天的收入以300元为标准,超过的钱数记作正数,不足的钱数记作负数,7天的收入记录如下: . (单位:元)(1)、收入最多的一天比最少的一天多多少元?(2)、小王这7天的地摊收入是盈利还是亏损?盈利或亏损多少元?20. 已知 , .(1)、化简 ,(2)、当与是同类项时,求的值.21. 某班计划买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价100元,乒乓球每盒定价20元.经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠,该班需球拍5副,乒乓球若干盒(不少于5盒).(1)、若该班需购买乒乓球x盒,用含x的式子分别表示在甲、乙两家商店购买的费用.(2)、当分别购买20盒、30盒乒乓球时,去哪家商店购买更合算?
