四川省绵阳市名校共同体2021-2022学年七年级上学期期末考试数学试题
试卷更新日期:2022-12-06 类型:期末考试
一、单选题
-
1. ﹣ 的相反数是( )A、﹣ B、﹣ C、 D、2. 2021年10月16日0时23分,长征二号F遥十三运载火箭,在酒泉卫星发射中心按照预定时间精准点火发射,将神舟十三号送入近地点高度200000m,远地点高度356000m的近地轨道,并与天和核心舱对接.其中数字356000用科学记数法表示为( )A、 B、 C、 D、3. 比( )A、大3 B、大7 C、小3 D、小4. 如图,分别从正面、左面、上面观察圆柱,得到的平面图形中,正确的是( )
 A、圆、长方形、三角形 B、长方形、长方形、圆 C、圆、三角形、长方形 D、长方形、圆、长方形5. 下列等式变形正确的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么6. 好又顺文具店中的必胜笔袋原价元,暑假期间这种笔袋滞销,文具店降价15%,因9月初开学季,必胜笔袋供不应求,该文具店又提价10%,现在这种笔袋的价格是( )A、 B、 C、 D、7. 如图,点在点的北偏东60°方向上,若和互余,在点处观察点 , 则点所在的方向是( )
A、圆、长方形、三角形 B、长方形、长方形、圆 C、圆、三角形、长方形 D、长方形、圆、长方形5. 下列等式变形正确的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么6. 好又顺文具店中的必胜笔袋原价元,暑假期间这种笔袋滞销,文具店降价15%,因9月初开学季,必胜笔袋供不应求,该文具店又提价10%,现在这种笔袋的价格是( )A、 B、 C、 D、7. 如图,点在点的北偏东60°方向上,若和互余,在点处观察点 , 则点所在的方向是( ) A、北偏东30° B、南偏西150° C、北偏西30° D、西偏北30°8. 如图,数轴上从左至右依次排列的三个点 , , , 其中、两点到原点的距离相等,且 , , 则点表示的数为( )
A、北偏东30° B、南偏西150° C、北偏西30° D、西偏北30°8. 如图,数轴上从左至右依次排列的三个点 , , , 其中、两点到原点的距离相等,且 , , 则点表示的数为( ) A、 B、1 C、 D、9. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”中,把“洛书”用今天的数学符号翻译出来,就是一个三阶幻方.请你探究如图洛书三阶幻方中,奇数和偶数的位置、数和数之间的数量关系所呈现的规律,根据这一规律,求出 , , 则( )
A、 B、1 C、 D、9. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”中,把“洛书”用今天的数学符号翻译出来,就是一个三阶幻方.请你探究如图洛书三阶幻方中,奇数和偶数的位置、数和数之间的数量关系所呈现的规律,根据这一规律,求出 , , 则( )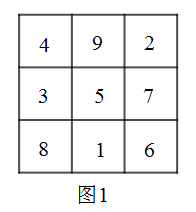
 A、16 B、8 C、 D、10. 两条直角边长度分别为3cm,4cm的直角三角形,绕其中一条直角边旋转一周,得到立体图形的体积(锥体的体积公式:)较大的是( )A、 B、 C、 D、11. 20名学生在进行一次科学实践活动时,需要组装一种实验仪器,仪器是由三个部件和两个部件组成.在规定时间内,每人可以组装好10个部件或20个部件.那么,在规定时间内,最多可以组装出实验仪器的套数为( )A、 50 B、60 C、100 D、15012. 在同一平面内,点在直线上,与互补, , 分别为 , 的平分线,若 , 则( )A、 B、 C、 D、
A、16 B、8 C、 D、10. 两条直角边长度分别为3cm,4cm的直角三角形,绕其中一条直角边旋转一周,得到立体图形的体积(锥体的体积公式:)较大的是( )A、 B、 C、 D、11. 20名学生在进行一次科学实践活动时,需要组装一种实验仪器,仪器是由三个部件和两个部件组成.在规定时间内,每人可以组装好10个部件或20个部件.那么,在规定时间内,最多可以组装出实验仪器的套数为( )A、 50 B、60 C、100 D、15012. 在同一平面内,点在直线上,与互补, , 分别为 , 的平分线,若 , 则( )A、 B、 C、 D、二、填空题
-
13. 下列各数: , , , 其中有理数有个.14. 在 , , , 2022,四个代数式中,单项式有个.15. 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“”一面与相对面上的代数式相等,则有“”一面与相对面上的代数式的和等于(用数字作答).
 16. 由成都开往北京的和谐号动车上共有人,在西安停站后,上车人数是下车人数的5倍,列车驶离西安站时动车上共有人,那么下车的人数有(用含 , 的式子表示).17. 如图,点 , , 在同一直线上, , , , 则.
16. 由成都开往北京的和谐号动车上共有人,在西安停站后,上车人数是下车人数的5倍,列车驶离西安站时动车上共有人,那么下车的人数有(用含 , 的式子表示).17. 如图,点 , , 在同一直线上, , , , 则. 18. 商场元旦节促销,购物原价不超过200元打九折,超过200元立减30元,小刚的妈妈结账时付款180元,则她购买的商品原价为元.
18. 商场元旦节促销,购物原价不超过200元打九折,超过200元立减30元,小刚的妈妈结账时付款180元,则她购买的商品原价为元.三、解答题
-
19. 计算:.20. 解方程:.21. 先化简,再求值:.(1)、若 , 求的值;(2)、若的平方比它本身还要大3,求的值.22. 如图,点是直线上一点, , 在直线的异侧,且 , 平分 , 平分.
 (1)、若 , 求和的度数;(2)、设 , 用含的式子表示.23. 如图,数轴上A,B两点表示的数分别是m,n满足.点P从A点出发以每秒2个单位的速度往点B的方向运动,点P出发1秒后,点Q从点B出发往点A的方向运动,设点Q的运动时间为t秒,点出发3秒钟后,点Q恰好位于线段PB的中点处.
(1)、若 , 求和的度数;(2)、设 , 用含的式子表示.23. 如图,数轴上A,B两点表示的数分别是m,n满足.点P从A点出发以每秒2个单位的速度往点B的方向运动,点P出发1秒后,点Q从点B出发往点A的方向运动,设点Q的运动时间为t秒,点出发3秒钟后,点Q恰好位于线段PB的中点处. (1)、求m,n的值,并求线段AB的长度;(2)、点Q每秒运动多少个单位长度?(3)、当BQ=2PQ时,求t的值.24. 有四个球队进行单循环比赛,每两队之间只比赛一场,每场比赛实行三局两胜制,即三局中获胜两局就获胜该场比赛,同时停止本场比赛.例如:表中第二行,比分表示队以战胜队.已知球队在每场比赛中都能获得积分,不同比分的积分不同,且积分为正整数.得到的比赛总积分表如下:
(1)、求m,n的值,并求线段AB的长度;(2)、点Q每秒运动多少个单位长度?(3)、当BQ=2PQ时,求t的值.24. 有四个球队进行单循环比赛,每两队之间只比赛一场,每场比赛实行三局两胜制,即三局中获胜两局就获胜该场比赛,同时停止本场比赛.例如:表中第二行,比分表示队以战胜队.已知球队在每场比赛中都能获得积分,不同比分的积分不同,且积分为正整数.得到的比赛总积分表如下:总积分
9
7
(1)、某球队要取得一场比赛的胜利,可能的比分结果是什么?(2)、若比分为时,净胜球为2,比分为时,净胜球为1,依此类推,净胜球越多,积分也越多.请你根据表格中的数据,求出各种比分对应的积分分别是什么?(3)、在(2)的条件下,若球队战胜了球队 , 但总积分 , 求 , 的值.