安徽省宿州市萧县2022-2023学年七年级上学期11月期中数学试题
试卷更新日期:2022-12-06 类型:期中考试
一、单选题
-
1. 立方根为( )A、 B、 C、 D、2. 若正比例函数的图象经过点 , 则k的值是( )A、-1 B、1 C、-4 D、43. 下列各组数中,以它们为边长的线段能构成直角三角形的是( )A、1,2,3 B、1, , C、4,5,6 D、12,15,204. 估计的值介于( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间5. 下列运算正确的是( )A、 B、 C、 D、6. 若最简二次根式与是可以合并的二次根式,则的值为( )A、5 B、 C、-2 D、7. 对于一次函数 , 下列说法错误的是( )A、图象不经过第一象限 B、图象与y轴的交点坐标为 C、图象可由直线向下平移2个单位长度得到 D、若点在一次函数的图象上,则8. 明明和亮亮一起下五子棋,明明持黑棋,亮亮持白棋.如图,若棋盘正中间的白棋的位置用表示,最右上角的黑棋的位置用表示,明明把第七枚圆形棋子放在适当位置,使所有棋子组成轴对称图形、则第七枚圆形棋子放的位置不可能是( )
 A、 B、 C、 D、9. 如图,在3×3的正方形网格中,每个小正方形的边长为1,A,B,C均为格点(网格线的交点),以点A为圆心,的长为半径作弧,交格线于点D,则的长为( )
A、 B、 C、 D、9. 如图,在3×3的正方形网格中,每个小正方形的边长为1,A,B,C均为格点(网格线的交点),以点A为圆心,的长为半径作弧,交格线于点D,则的长为( ) A、 B、 C、 D、10. 如图,佳佳设计了一种挖宝游戏,屏幕上正方形是宝藏区(含正方形边界),其中 , , 沿直线行走,则游戏者能够挖到宝藏的b的取值范围为( )
A、 B、 C、 D、10. 如图,佳佳设计了一种挖宝游戏,屏幕上正方形是宝藏区(含正方形边界),其中 , , 沿直线行走,则游戏者能够挖到宝藏的b的取值范围为( ) A、 B、 C、 D、
A、 B、 C、 D、二、解答题
-
11. 计算:.12. 电流通过导线时会产生热量,且满足 , 其中Q为产生的热量(单位J),I为电流(单位∶A),R为导线电阻(单位∶Ω),t为通电时间(单位∶s),若导线电阻为 , 时间导线产生的热量,求电流的值.13. 如图,甲、乙两船从港口A同时出发,甲船以16海里/时的速度向北偏东42°方向航行,乙船向南偏东48°方向航行,0.5小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距17海里,问乙船的航速是多少?
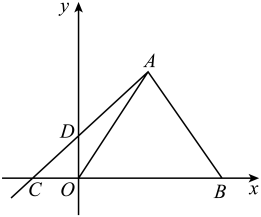
 14. 已知点 .(1)、若点与点的连线与轴平行,求点的坐标.(2)、若的平方根是±3,直线经过点 , 求的值.15. 甲、乙两家体育用品商店出售相同的乒乓球和乒乓球拍,乒乓球每盒定价20元,乒乓球拍每副定价100元.现两家商店都搞促销活动,甲店每买一副球拍赠两盒乒乓球,乙店按八折优惠.某俱乐部需购球拍4副,乒乓球盒.(1)、若在甲店购买付款(元),在乙店购买付款(元),分别写出 , 与x的函数关系式.(2)、若该俱乐部需要购买乒乓球30盒,在哪家商店购买合算?16. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)的顶点A,B 的坐标分别为 .
14. 已知点 .(1)、若点与点的连线与轴平行,求点的坐标.(2)、若的平方根是±3,直线经过点 , 求的值.15. 甲、乙两家体育用品商店出售相同的乒乓球和乒乓球拍,乒乓球每盒定价20元,乒乓球拍每副定价100元.现两家商店都搞促销活动,甲店每买一副球拍赠两盒乒乓球,乙店按八折优惠.某俱乐部需购球拍4副,乒乓球盒.(1)、若在甲店购买付款(元),在乙店购买付款(元),分别写出 , 与x的函数关系式.(2)、若该俱乐部需要购买乒乓球30盒,在哪家商店购买合算?16. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)的顶点A,B 的坐标分别为 .
⑴请在如图所示的网格中作出平面直角坐标系.
⑵请作出关于y轴对称的 .
⑶直接写出点的坐标.
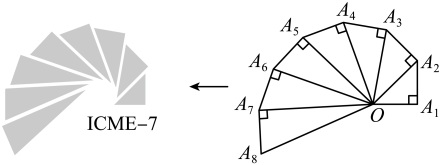
17. 观察以下等式···
按照以上规律,解决下列问题:
(1)、 =(2)、 =(3)、根据你的观察、猜想,写一个含n(n为正整数)的等式表示该规律,不用证明.(4)、利用这一规律计算:(写出计算过程)18. 某同学根据学习函数的经验,对函数的图像与性质进行了探究.下面是他的探究过程,请补充完整∶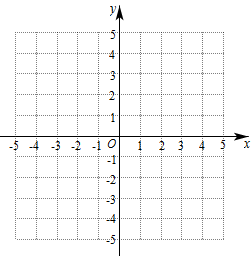 (1)、填表
(1)、填表x
…
-5
-4
-3
-2
-1
0
1
2
3
4
…
y
…
-1
-1
-1
0
1
3
…
(2)、根据(1)中的结果,请在所给坐标系中画出函数的图像.(3)、结合函数图象,请写出该函数的一条性质.19. 如图 (1)、如图,三个正方形围成了一个直角三角形,三个正方形的面积分别为 , 若 , 则(2)、如图,在中, , 分别以为边在外侧作等边三角形,则之间的关系为(3)、①如图,在中, , 分别以为边在外侧作等腰直角三角形,则(2)中的关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由.
(1)、如图,三个正方形围成了一个直角三角形,三个正方形的面积分别为 , 若 , 则(2)、如图,在中, , 分别以为边在外侧作等边三角形,则之间的关系为(3)、①如图,在中, , 分别以为边在外侧作等腰直角三角形,则(2)中的关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由.②如图,在五边形中, , 连接 . 求五边形的面积.
三、填空题