四川省绵阳市名校共同体2021-2022学年八年级上学期期末考试数学试题

试卷更新日期：2022-12-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下面是四家医院标志的图案部分，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在党中央的坚强领导下，经过两年的战斗，新型冠状病毒引发的肺炎疫情得到了有效控制.研究发现，某种新型冠状病毒的直径约为213纳米，1纳米 $= 1.0 \times 10^{- 9}$ 米，若用科学记数法表示213纳米，则正确的结果是（）

A、 $2.13 \times 10^{- 6}$ 米 B、 $0.213 \times 10^{- 6}$ 米 C、 $2.13 \times 10^{- 7}$ 米 D、 $21.3 \times 10^{- 7}$ 米

查看试题解析
3. 下列各式中，运算正确的是（）

A、 ${(- a^{3})}^{2} = - a^{6}$ B、 ${(- \frac{1}{2})}^{- 2} = 4$ C、 ${(- 2022)}^{0} = 2022$ D、 $a^{8} \div a^{4} = a^{2}$

查看试题解析
4. 下列结论正确的是（）

A、两个等边三角形全等 B、有一个锐角相等的两个直角三角形全等 C、有两边及一个角对应相等的两个三角形全等 D、斜边和一个锐角对应相等的两个直角三角形全等

查看试题解析
5. $- \frac{1}{2} x^{3} y^{- 1} \cdot {(- 2 x^{- 1} y)}^{2} =$ （）

A、 $- 2 x y$ B、 $2 x y$ C、 $- 2 x^{2} y$ D、 $2 x y^{2}$

查看试题解析
6. 在数学探究活动课中，清华同学如果要用小木棒钉制成一个三角形，其中两根小木棒长分别为2cm，3cm，则第三根小木棒可取（）

A、1cm B、2cm C、5cm D、6cm

查看试题解析
7. 如图，在 $△ A B C$ 中， $A D$ ， $A E$ 分别是边 $B C$ 上的中线和高，点 $D$ 在点 $E$ 的左侧，已知 $A E = 2 cm$ ， $D E = 1 cm$ ， $S_{△ A B C} = 8 {cm}^{2}$ ， $C E =$ （）

A、1cm B、2cm C、3cm D、4cm

查看试题解析
8. 若 $x^{2} + 2 (b - 1) x + 4$ 是完全平方式，且 $a = - 3$ ，则 $a^{b} =$ （）

A、 $- 27$ B、 $- 27$ 或27 C、27或 $- \frac{1}{3}$ D、 $- 27$ 或 $- \frac{1}{3}$

查看试题解析
9. 如图，在△ABC中，∠ABC=60°，BC=20，点D在边AB上，CA=CD，BD=8，则AD=（）

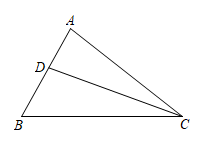A、2 B、3 C、4 D、6

查看试题解析
10. 已知3^m＝x，3²ⁿ＝y，m、n为正整数，则9^m＋2n＝（）

A、x²y² B、x²＋y² C、2x＋12y D、24xy

查看试题解析
11. 如图，在正五边形 $A B C D E$ 中，点 $F$ 是 $C D$ 的中点，点 $G$ 在线段 $A F$ 上运动，连接 $E G$ ， $D G$ ，当 $△ D E G$ 的周长最小时，则 $∠ E G D =$ （）

A、36° B、60° C、72° D、108°

查看试题解析
12. 如图，在△ABC中，∠ABC和∠ACB的角平分线交于点O，AD经过点O与BC交于点D，以AD为边向两侧作等边△ADE和等边△ADF，分别和AB，AC交于点G，H，连接GH.若∠BOC=120°，AB=a，AC=b，AD=c.则下列结论中正确的个数有（）

①∠BAC=60°；②△AGH是等边三角形；

③AD与GH互相垂直平分；④ $S_{△ A B C} = \frac{1}{2} (a + b) c$ .

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 分解因式： $a^{2} b - 2 a b^{2} + b^{3} =$ .

查看试题解析
14. 如图，在三角形纸片 $A B C$ 中， $A C = 6 cm$ ，沿过点 $B$ 的直线折叠这个三角形，使顶点 $C$ 落在边 $A B$ 上的点 $E$ 处，折痕为 $B D$ ， $A E = 3 cm$ ，则 $△ A E D$ 的周长等于cm.

查看试题解析
15. 若分式 $\frac{3 - | x |}{x + 3}$ 的值为零，则x的值为．

查看试题解析
16. 如图，在等腰△ABC中，AB=BC=a，CE=b，∠BAC和∠ABC的平分线分别为AD，BE相交于点O，AD交BC于点D，BE交AC于点E，过点O作OF⊥AB于F，若OF=c，则△ABC的面积为.

查看试题解析
17. 如图，在四边形ABCD中，点F在BC的延长线上，∠ABC的平分线和∠DCF的平分线交于点E，若∠A+∠D=224°，则∠E=.

查看试题解析
18. 若关于 $x$ 的方程 $\frac{1}{x + 1} - \frac{a}{x - 3} = \frac{2 (a - 1)}{x^{2} - 2 x - 3}$ 的解为整数，则满足条件的所有整数 $a$ 的和等于.

查看试题解析

三、解答题

19.

(1)、计算： $[{(x - y)}^{2} - (x + y) (x - y)] \div (- 2 y) + 2 y$ .

(2)、解分式方程： $\frac{2 x}{2 x + 3} + \frac{2}{2 x - 3} = 1$ .

查看试题解析
20. 先化简，再求值： $\frac{a^{2} + 4 a + 4}{a^{2} + a} \div (\frac{3}{a + 1} - a + 1) \cdot \frac{2 - a}{a + 2}$ ，其中点 $(a ， 3)$ 关于 $y$ 轴的对称点是 $(4 ， 3)$ .

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ A C B = 60 °$ ，点D在 $A C$ 上， $B C = C D$ ，以 $A B$ 为边向左侧作等边三角形 $A B E$ ，连 $E D$ .

(1)、求证： $△ A B C ≌ △ E B D$ ；

(2)、过点B作 $B F ⊥ E D$ 于点F， $D F = 2$ ，求 $B D$ 的长.

查看试题解析
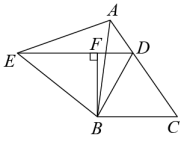22. 精强硅谷，有众多高科技产业，红旗电子科技公司是通讯设备、电源设备及消费类电子产品生产厂商，提供各类高分子材料、热传导材料、绝缘材料、缓冲及防尘材料.该公司今年承包了一手机品牌某一热传导材料零部件的生产任务，原计划在规定时间内生产24000个热传导材料零部件，由于此零件紧缺，需要提前5天供货，该公司经商议后，决定将工作效率比原计划提高25%，结果按预期刚好提前5天完成任务，求原计划每天生产的零件个数和规定的天数.

查看试题解析
23. 如图，在△ABC中，AB=AC，CE平分∠ACB交AB于点D，点D在AC的垂直平分线上，过点E作EF⊥BC交CB的延长线于点F，CE=AC，BC=AD.

(1)、求证：∠BEC=∠BAC；

(2)、求∠CAE的度数；

(3)、若BF=3，求BD的长.

查看试题解析
24. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ，点 $D$ 是 $A B$ 上一动点，连接 $C D$ ，以点 $C$ 为直角顶点， $C D$ 为直角边作等腰直角 $△ D C E$ ， $D E$ 交 $B C$ 于点 $F$ .

(1)、如图1，若 $∠ B = 20 °$ ，当 $△ C D F$ 为等腰三角形时，请直接写出此时 $∠ B D F$ 的度数；

(2)、如图2，若 $E D ⊥ A B$ ，点 $G$ 为 $E F$ 上一点， $B D + G E = F G$ .
①求证： $∠ B F D = ∠ A$ ；

②求证： $A B = 2 F G$ .

查看试题解析