四川省达州市渠县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-12-06 类型:期末考试
一、单选题
-
1. 下列各数中最小的是( )A、 B、 C、 D、02. 点 关于y轴的对称点是( )A、 B、 C、 D、3. 如图,雷达探测器测得六个目标出现,按照规定的目标表示方法,目标的位置表示为 , 按照此方法在表示目标的位置时,其中表示不正确的是( )
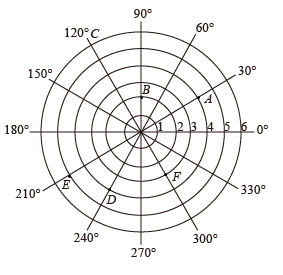 A、 B、 C、 D、4. 在防控心冠病毒疫情中,对八年级某班所有学生测量了一次体温(单位:),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
A、 B、 C、 D、4. 在防控心冠病毒疫情中,对八年级某班所有学生测量了一次体温(单位:),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
体温
36.1
36.2
36.3
36.4
36.5
36.6
人数
4
8
8
10
x
2
A、这些体温的众数是 B、这些体温的中位数是 C、这个班有40名学生 D、5. 下列各式计算正确的是( )A、 B、 C、 D、6. 在中, , 则的度数为( )A、 B、 C、 D、7. 20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是( )A、 B、 C、 D、8. 关于x,y的方程组的解是 , 其中y的值被盖住了,不过仍能求出m,则m的值是( )A、 B、 C、 D、9. 关于x的方程kx+b=3的解为x=7,则直线y=kx+b的图象一定过点( )A、(3,0) B、(7,0) C、(3,7) D、(7,3)10. 一次长跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之是的函数关系如图,则这次长跑的全程为( )米.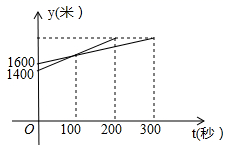 A、2000米 B、2100米 C、2200米 D、2400米
A、2000米 B、2100米 C、2200米 D、2400米二、填空题
-
11. 一个数的平方等于64,则这个数的立方根是.12. 一组数据的平均数为5,则这组数据的极差为;13. 试写出一个一次函数,使其满足以下条件:(1)过(3,2);(2)y随x的增大而减小.这个一次函数可以是.14. 一架 长的梯子斜靠在一竖直的墙上,这时梯足距离墙底 ,如果梯子的顶端沿墙下滑 ,那么梯足将滑 :15. 已知和关于原点对称,则.16. 如图,已知( , 且),在的两边上各任取一点,分别记为 , 过该两点分别引一条直线,并使得该直线与所在的边夹角也为 , 设两条直线交于点O,则的数量应是.

三、解答题
-
17. 计算:(1)、(2)、 .18. 解下列方程组:(1)、(2)、19. 我市某中学举办“网络安全知识竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示:

平均分(分)
中位数(分)
众数(分)
方差
初中部
a
85
b
高中部
85
80
100
160
(1)、根据图示求出a,b的值;(2)、结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?(3)、计算初中代表队决赛成绩的方差 , 并判断哪一个代表队选手成绩较为稳定.20. 在如图所示的正方形网格中,每个小正方形的边长都为1,格点三角形ABC(顶点是网格线的交点的三角形)的顶点A、C的坐标分别为(-4,5)、(-1,3).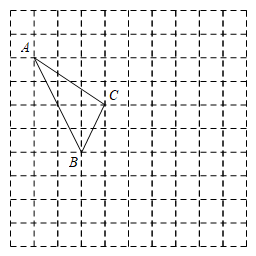 (1)、请在网格平面内作出平面直角坐标系;(2)、请作出ABC关于y轴对称的;(3)、点的坐标为;(4)、 的面积为.21. 如图,有三个论断:①;②;③ , 请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
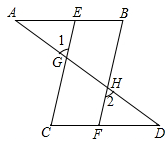
(1)、请在网格平面内作出平面直角坐标系;(2)、请作出ABC关于y轴对称的;(3)、点的坐标为;(4)、 的面积为.21. 如图,有三个论断:①;②;③ , 请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.已知: ▲ .结论: ▲ .
理由:
 22. 今年“五一”小长假期间,某市外来与外出旅游的总人数为287万人,分别比去年同期增长和 , 去年同期外来旅游比外出旅游的人数多20万人.求该市今年外来和外出旅游的人数.23. 国家推行“节能减排,低碳经济”政策后,某企业推出一种“CNG”改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)(元)与正常运营时间x(天)之间分别满足关系式: , 图象如图所示.
22. 今年“五一”小长假期间,某市外来与外出旅游的总人数为287万人,分别比去年同期增长和 , 去年同期外来旅游比外出旅游的人数多20万人.求该市今年外来和外出旅游的人数.23. 国家推行“节能减排,低碳经济”政策后,某企业推出一种“CNG”改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)(元)与正常运营时间x(天)之间分别满足关系式: , 图象如图所示. (1)、每辆车改装前每天的燃料费元,每辆车的改装费元,正常运营时间天后,就可以从节省的燃料费中收回改装成本;(2)、某出租汽车公司一次性改装了100辆出租车,因而正常运行多少天后共节省燃料费60万元?
(1)、每辆车改装前每天的燃料费元,每辆车的改装费元,正常运营时间天后,就可以从节省的燃料费中收回改装成本;(2)、某出租汽车公司一次性改装了100辆出租车,因而正常运行多少天后共节省燃料费60万元?

