四川省成都市天府新区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-12-06 类型：期末考试

进入出卷网下载

一、单选题

1. 四个实数 $- 2$ ， 0， $- \sqrt{2}$ ， $- 1$ 中，最大的实数是（）．

A、 $- 2$ B、0 C、 $- \sqrt{2}$ D、 $- 1$

查看试题解析
2. 4的平方根是（）

A、2 B、±2 C、16 D、±16

查看试题解析
3. 估计 $\sqrt{14}$ 的值在（　　）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
4. 下列各组数中，不能作为直角三角形的三边长的是（　　）

A、1，2， $\sqrt{3}$ B、5，4，3 C、17，8，15 D、2，3，4

查看试题解析
5. 使 $\sqrt{x - 3}$ 有意义的x的取值范围是（）

A、x≤3 B、x＜3 C、x≥3 D、x＞3

查看试题解析
6. 点P关于x轴对称点P₁的坐标是（4，-8），则P点的坐标是（）

A、（4，8） B、（-4，-8） C、（-4，8） D、（4，-8）

查看试题解析
7. 如图，BD平分∠ABC，若∠1＝∠2，则（）

A、AD＝BC B、AB＝CD C、AB∥CD D、AD∥BC

查看试题解析
8. 气象局调查了甲、乙、丙、丁四个城市连续四年的降水量，它们的平均降水量都是323毫米，方差分别是 $S_{甲}^{2} = 3.2$ ， $S_{乙}^{2} = 5.1$ ， $S_{丙}^{2} = 3.1$ ， $S_{丁}^{2} = 6.9$ ，则这四个城市年降水量最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 《九章算术》是中国古代第一部数学专著，它对我国古代后世的数学家产生了深远的影响.该书中记载了一个问题，大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元.问有多少人?该物品价几何?设有x人.物品价值y元，则列方程组为（）

A、 ${\begin{array}{l} 8 x + 3 = x \\ 7 y - 4 = x \end{array}$ B、 ${\begin{array}{l} 8 x + 3 = y \\ 7 y - 4 = y \end{array}$ C、 ${\begin{array}{l} 8 y - 3 = x \\ 7 y + 4 = x \end{array}$ D、 ${\begin{array}{l} 8 x - 3 = y \\ 7 x + 4 = y \end{array}$

查看试题解析
10. 已知直线l₁：y=kx+b与直线l₂：y=-2x+4交于点C（m，2），则方程组 ${\begin{array}{l} y = k x + b \\ y = - 2 x + 4 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$

查看试题解析

二、填空题

11. $- \sqrt{21}$ 的相反数是．

查看试题解析
12. 点A（2，-3）到y轴的距离是 .

查看试题解析
13. 汽车开始行驶时，油箱中有油30升，如果每小时耗油4升，那么油箱中的剩余油量y(升)和工作时间x（时）之间的函数关系式是；

查看试题解析
14. 如图，在△ABC中，按以下步骤作图：①以点C为圆心，任意长为半径作弧，分别交AC，CB于点E和F；②分别以E，F为圆心，大于 $\frac{1}{2}$ EF为半径画弧，两弧交于点D；③作射线CD交AB于点G；延长CA至H，使CH＝CB，连接HG，若AH＝2，AB＝5，则△AHG的周长为 .

查看试题解析
15. 若a，b为实数，且 $\sqrt{a + 1} +$ （10-b）²＝0，则 $\sqrt{a + b} =$ .

查看试题解析
16. 已知一次函数y＝（k+3）x+k²-9的图象经过原点，则k的值为 .

查看试题解析
17. 若关于x，y的二元一次方程组 ${\begin{array}{l} x + y = 3 k \\ x - y = k \end{array}$ 的解也是二元一次方程x+2y＝1的解，则k的值为 .

查看试题解析
18. 已知，如图，在平面直角坐标系xOy中，直线l₁：y＝x+3分别交x轴，y轴于点A，B两点，直线l₂：y＝-3x过原点且与直线l₁相交于C，点P为y轴上一动点.当PA+PC的值最小时，点P的坐标为 .

查看试题解析
19. 如图，正方形ABCD的边长为2，E是边BC上的一点，连接AE，将点E绕点A顺时针旋转使得E点的对应点F落在CB的延长线上，连接AF，过点F作AE的垂线，交对角线AC于点G，若AG＝2CG，则线段EF的长为 .

查看试题解析

三、解答题

20.

(1)、计算：|1 $- \sqrt{2}$ | $+ \sqrt{9} -$ （ $\frac{1}{3}$ ）^-¹+（ $\sqrt{5} -$ 2）⁰；

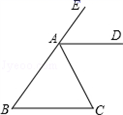
(2)、解方程组： ${\begin{array}{l} 2 x - y = 7 \\ 3 x + 2 y = 0 \end{array}$ .

查看试题解析
21. 已知：如图，在△ABC中，∠B=∠C，AD平分外角∠EAC．
求证：AD∥BC．

查看试题解析
22. 如图，在直角坐标平面内，△ABC的三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）.

(1)、S_△ABC＝；

(2)、画出△ABC关于x轴的对称图形△A₁B₁C₁ ，再画出△A₁B₁C₁关于y轴的对称图形△A₂B₂C₂.

查看试题解析
23. 自2021年“双减”政策实施以来，天府新区各学校积极推动“双减”工作，落实教育部文件精神，减轻学生作业负担.为了解实施成效，天府新区某调查组随机调查了某学校部分同学完成家庭作业的时间，设完成的时间为x小时，为方便统计，完成的时间x≤0.5范围内一律记为0.5小时，完成的时间0.5＜x≤1范围内一律记为1小时，完成的时间1＜x≤1.5范围内一律记为1.5小时，完成的时间x＞1.5一律记为2小时，根据调查得到的数据绘制了不完整的统计图，根据图中信息回答下列问题：

(1)、将条形统计图补充完整；

(2)、写出抽查的学生完成家庭作业时间的众数和中位数；

(3)、计算调查学生完成家庭作业的平均时间.

查看试题解析
24. 某校组织“大手拉小手，义卖献爱心”活动，计划购买黑白两种颜色的文化衫进行手绘设计后出售，并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花4800元购买了黑白两种颜色的文化衫200件，每件文化衫的批发价及手绘后的零售价如表：

批发价(元)

零售价(元)

黑色文化衫

25

45

白色文化衫

20

35

(1)、学校购进黑.白文化衫各几件？

(2)、通过手绘设计后全部售出，求该校这次义卖活动所获利润.

查看试题解析
25. 如图，在平面直角坐标系中，直线y＝kx过点B（m，6），过点B分别作x轴和y轴的垂线，垂足分别为点A，C，∠AOB＝30°.动点P从点O出发，以每秒2个单位长度的速度向点B运动，动点Q从点B出发.以每秒 $\sqrt{3}$ 个单位长度的速度向点C运动.点P，Q同时开始运动，当点P到达点B时，点P，Q同时停止运动，设运动时间为t秒.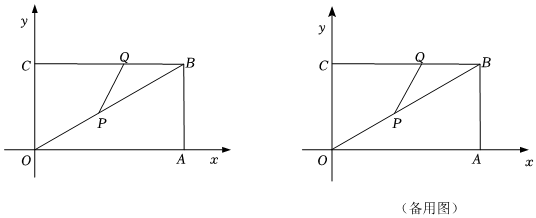

(1)、求m与k的值；

(2)、设△PQB的面积为S，求S与t的关系式；

(3)、若以点P，Q，B为顶点的三角形是等腰三角形，请求出t的值.（温擎提示：在直角三角形中，30°的角所对的直角边等于斜边的一半）

查看试题解析
26. 近年来，四川天府新区取得了飞速的发展，以成都科学城发展为例，兴隆湖畔集结了一大批领先的科技创新领军项目，正如火如荼地推进建设，据报道，新区某公司打算购买A，B两种花装点城区道路，公司负责人到花卉基地调查发现：购买1盆A种花和2盆B种花需要14元，购买2盆A种花和1盆B种花需要13元.

(1)、求A，B两种花的单价各为多少元？

(2)、公司若购买A，B两种花共10000盆，设购买的A种花m盆（3000≤m≤5000），总费用为W元；
①求W与m的关系式；

②请你帮公司设计一种购花方案，使总花费最少？并求出最少费用为多少元？

查看试题解析
27. 已知，如图，△ABC和△ADE是两个完全相同的等腰直角三角形，且∠ABC＝∠AED＝90°；

(1)、如图1，当△ADE的AD边与△ABC的AB边重合时，连接CD，求∠BCD的度数；

(2)、如图2，当A，B，D不在一条直线上时，连接CD，EB，延长EB交CD于F，过点A作AG⊥EB，垂足为点G，过点D作DT⊥EB，垂足为点T，求证：EG＝FT；

(3)、在（2）的条件下，若AF＝3，DF＝2，求EF的长.

查看试题解析
28. 已知，如图1，直线AB分别交平面直角坐标系中x轴和y轴于A，B两点，点A坐标为（-3，0），点B坐标为（0，6），点C在直线AB上，且点C坐标为（-a，a），

(1)、求直线AB的表示式和点C的坐标：

(2)、点D是x轴上的一动点，当S_△AOB＝S_△ACD时，求点D坐标；

(3)、如图2，点E坐标为（0，-1），连接CE，点P为直线AB上一点，且∠CEP＝45°，求点P坐标.

查看试题解析

	批发价(元)	零售价(元)
黑色文化衫	25	45
白色文化衫	20	35