四川省成都市邛崃市2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-12-06 类型：期末考试

进入出卷网下载

一、单选题

1. 有理数 $4$ 的绝对值为（）.

A、 $- 4$ B、 $4$ C、 $\frac{1}{4}$ D、 $- \frac{1}{4}$

查看试题解析
2. 为了解本地区老年人的健康状况，下列选取的调查对象最合适的是（）

A、在公园里调查100名老人 B、在广场舞队伍里调查100名老人 C、在医院调查100名老人 D、在派出所的户籍网随机调查100名老人

查看试题解析
3. 如图，从A地前往B地有三条道路a、b、c，但走b这条路最近，理由是（）

A、两点之间，线段最短 B、两点之间，射线最短 C、两点之间，直线最短 D、两点确定一条直线

查看试题解析
4. 如图，当时钟指向4：00时，钟面上时针与分针的夹角是（）

A、140° B、130° C、120° D、100°

查看试题解析
5. 若 $x = 5$ 是关于x的一元一次方程 $x + a = 2$ 的解，则常数a的值为（）

A、3 B、2 C、 $- 3$ D、 $- 2$

查看试题解析
6. 下列图形经过折叠能围成一个正方体的是（）

A、 B、 C、 D、

查看试题解析
7. 据2021年11月9日新华社消息，天问一号环绕器开展火星全球遥感探测，截至11月8日，环绕器在轨运行473天，地球与火星的距离为384000000千米，数字384000000用科学记数法表示为（）

A、 $38 ． 4 \times 10^{7}$ B、 $384 \times 10^{6}$ C、 $3 ． 84 \times 10^{8}$ D、 $3 ． 84 \times 10^{9}$

查看试题解析
8. 根据“x与1的差比x的3倍多2”可列方程为（）

A、 $x - 1 = 3 x + 2$ B、 $x + 1 = 3 x + 2$ C、 $x - 1 = 3 x - 2$ D、 $x - 1 = 3 (x + 2)$

查看试题解析
9. 下列计算正确的是（）

A、 $2 x + 3 y = 5 x y$ B、 $3 x^{2} + 2 x^{2} = 5 x^{4}$ C、 $- 2 (x - 2 y) = - 2 x - 2 y$ D、 $- x^{2} y + 2 x^{2} y = x^{2} y$

查看试题解析
10. 相传大禹时期，洛阳市西洛宁县洛河中浮出神龟，背驮“洛书”，献给大禹，大禹依此治水成功，遂划天下为九州.图1是我国古代传说中的洛书，图2是洛书的数字表示，洛书是一个三阶幻方，就是将已知的9个数填入 $3 \times 3$ 的方格中，使每一行、每一竖列以及两条斜对角线上的数字之和都相等.在图3的幻方中也有类似于图1的数字之和的这个规律，则 $a + b$ 的值为（）

A、2 B、 $- 2$ C、4 D、6

查看试题解析

二、填空题

11. 三棱柱有个面，条棱.

查看试题解析
12. 如图，数轴上的点A表示的数是 $- 3$ ，将点A向右移动5个单位长度，此时点A表示的数是·

查看试题解析
13. 已知 $a + b = - 2$ ，则代数式 $3 + a + b$ 的值为.

查看试题解析
14. 从六边形的一个顶点可引出条对角线．

查看试题解析
15. 用平面去截一个几何体，如果截面的形状是圆形，则这个几何体可能是（写出所有可能结果的正确序号）.①球；②正方体；③圆柱；④圆锥；⑤五棱柱

查看试题解析
16. a、b、c三数在数轴上的位置如图所示，化简 $| a + b | - | b - c | =$ .

查看试题解析
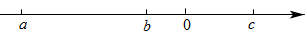17. 按如图所示的程序进行计算，计算按箭头指向循环进行，当初始输入为5时，第2021次计算的结果为.

查看试题解析
18. 元旦节期间，某商场对顾客实行这样的优惠政策：若一次购物不超过200元，则不予折扣；若一次购物超过200元不超过500元，则按标价给予八折优惠：若一次购物超过500元，其中500元按上述八折优惠外，超过500元的部分给予七折优惠.小明的妈妈两次购物分别付款192元和384元，如果她合起来一次性购买同样多的商品，那么她可以节约元.

查看试题解析
19. 如图，已知A，B两点在数轴上，点A表示的数是 $- 5$ ， $O B = 3 O A$ ，动点P从点A出发，以每秒1个单位的速度沿线段AB向终点B运动，同时，另一个动点Q从点B出发，以每秒3个单位的速度在线段AB上来回运动（从点B向点A运动，到达点A后，立即原速返回，再次到达B点后立即掉头向点A运动，掉头时间忽略不计）.当点P达到点B时，P、Q两点都停止运动.当点P运动秒时，点Q恰好落在线段AP的中点上.

查看试题解析

三、解答题

20.

(1)、计算： $\frac{1}{4} \times (- 8) + 16 \div {(- 2)}^{3}$ ；

(2)、解方程： $\frac{1}{4} (x - 2) - \frac{1}{7} (x + 4) = 0$ .

查看试题解析
21. 一个几何体由几个大小相同的小立方块搭成，请画出从正面、左面、上面看到的这个几何体的形状图.

查看试题解析
22. 先化简，再求值： $4 (x^{2} - x y + 6) - (5 x^{2} - 3 x y) - 24$ ，其中 $x = - 2$ ， $y = 1$ .

查看试题解析
23. 如图，点C是线段AB上一点， $A C > B C$ ，点M是线段AB的中点，点N是线段BC的中点， $A M = 8$ ， $C N = 3$ ，求线段MN的长度.

查看试题解析
24. 为了解同学们更喜欢什么球类运动，以便学校组织受同学们欢迎的比赛，学生会体育部的部长小强随机调查了部分同学对五种球类运动（A：篮球、B：足球、C：排球、D：乒乓球、E：羽毛球）的喜欢程度，并将结果绘制成如下两幅不完整的统计图.

(1)、此次共调查了名学生；

(2)、扇形统计图中，D：乒乓球所对应的扇形圆心角的大小为度；

(3)、通过计算补全条形统计图；

(4)、学校共有980名学生，估计该校学生喜欢篮球的有多少人？

查看试题解析
25. 将连续的偶数0，2，4，6，8，…排成如图所示的数表.

(1)、十字形框内的五个数之和是中间数的；若设十字形框内的五个数中最中间一个数是x，用代数式表示十字形框内五个数之和为；

(2)、若将十字形框上下左右移动，可框住另外五个数，这五个数还有上述规律吗？直接写出答案，不需要证明；

(3)、十字形框能否框到五个数，使这五个数之和等于2400呢？若能，请写出这五个数，若不能，请说明理由.

查看试题解析
26. 亮亮家买了新房，如图是房屋的平面图，根据图中的数据（单位：m），解答下列问题：

(1)、用含x、y的代数式表示厨房的面积为m² ，卫生间的面积为m²：若图中x、y的值满足 $| x - 3 | + | 2 - y | = 0$ ，厨房和卫生间的总面积为m².

(2)、亮亮的爸爸打算在两个卧室内的四周贴上墙纸（门和窗户忽略不计），已知房间的高度是3米，求需要购买多少平方米的墙纸？

查看试题解析
27. 一副三角板ABC与DEF中， $∠ A = ∠ D = 90 °$ ， $∠ B = ∠ C = 45 °$ ， $∠ E = 30 °$ ， $∠ F = 60 °$ .

(1)、将这副三角板的点A与E重合，拼成如图1所示的图案，则 $∠ B C D =$ °； $∠ P A B =$ °； $∠ A P C =$ °；

(2)、将这副三角板的点C与点F重合，拼成如图2的图案，CN平分∠ACE，CM平分∠DCB，若 $∠ B C E = α$ ，求∠MCN的度数；

(3)、将图2中的三角板ABC绕点C顺时针旋转到图3的图案，若CN平分∠ACE，CM平分∠DCB，若 $∠ B C E = β$ ，求∠MCN的度数.

查看试题解析

28. 某中学为全体学生办理了“学生团体住院医疗保险”，保险公司按下表级距分段计算给付“住院医疗保险金”.

级数	被保人住院医疗费用级距	保险公司给付比例
1	1000元及以下部分	55%
2	1000元以上支4000元部分	60%
3	4000元以上至7000元部分	70%
4	7000元以上至10000元部分	80%
5	10000元以上至30000元部分	90%
6	30000元以上部分	95%
注：在保险期间，被保险人按上述标准累计自付金额超过6000元部分，保险公司按100%标准给付

例如：若住院医疗费用为3500元，则保险公司应给付的保险金为： $1000 \times 55 % + (3500 - 1000) \times 60 % = 550 + 1500 = 2050$ （元），则自付医疗费为 $3500 - 2050 = 1450$ （元）

(1)、若住院医疗费为1000元，则自付医疗费元；若住院医疗费为4000元，则保险公司应给付保险金元；若住院医疗费为7000元，则保险公司应给付保险金元；自付医疗费元·

(2)、刘茜同学生病住院，保险公司给付了3120元的住院医疗保险金，刘茜的住院医疗费是多少？

(3)、李强同学生病住院，他的父母共自付医疗费6000元，保险公司为李强同学给付了保险金多少元？

查看试题解析