四川省成都市简阳市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-12-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中的无理数是（）

A、0 B、 $\sqrt{9}$ C、 $π$ D、1.01010101…

查看试题解析
2. 若点P（2，﹣3），则点P关于原点的对称点的坐标是（）

A、（2，3） B、（﹣2，﹣3） C、（﹣2，3） D、（2，﹣3）

查看试题解析
3. 下列给出的四组数中，能构成直角三角形三边的一组是（）

A、3，4，5 B、5，12，14 C、6，8，9 D、8，13，15

查看试题解析
4. 下列等式成立的是（）

A、 $3 + 4 \sqrt{2} = 7 \sqrt{2}$ B、 $\sqrt{3} \times \sqrt{2} = \sqrt{5}$ C、 $\sqrt{3} \div \frac{1}{\sqrt{6}} = 2 \sqrt{3}$ D、 $\sqrt{{(- 3)}^{2}} = 3$

查看试题解析
5. 下列命题是真命题的是（）

A、如果两个角是内错角，那么它们一定相等 B、如果两个角是同位角，那么它们一定相等 C、如果两个角是同旁内角，那么它们一定互补 D、如果两个角是对顶角，那么它们一定相等

查看试题解析
6. 一次函数y＝7x-6的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 已知点（﹣2，y₁），（3，y₂）都在直线y＝﹣x﹣5上，则y₁ ， y₂的值的大小关系是（）

A、y₁＜y₂ B、y₁＞y₂ C、y₁＝y₂ D、不能确定

查看试题解析

8. 下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：

	甲	乙	丙	丁
平均数（环）	9.5	9.5	9.5	9.5
方差	8.5	7.3	8.8	7.7

根据表中数据，要从中选择一名成绩发挥稳定的运动员参加比赛，应选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

9. 如图，一次函数y＝2x和y＝ax+4的图象相交于点A（m，3），则关于x，y的方程组 ${\begin{matrix} y = 2 x \\ y = a x + 4 \end{matrix}$ 的解为（）

A、 ${\begin{matrix} x = \frac{3}{2} \\ y = 3 \end{matrix}$ B、 ${\begin{matrix} x = 3 \\ y = \frac{3}{2} \end{matrix}$ C、 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 3 \end{matrix}$

查看试题解析

二、填空题

10. 实数2﹣ $\sqrt{3}$ 的倒数是.

查看试题解析
11. 已知一次函数的图象经过点 $(0 ， 5)$ ，且与直线 $y = x$ 平行，则一次函数的表达式为.

查看试题解析
12. 《九章算术》是我国古代一部著名的算书，它的出现标志着中国古代数学形成了完整的体系其中卷八方程[七]中记载：“今有牛五、羊二，直金十两.牛二、羊五，直金八两.牛、羊各直金几何？”题目大意是：5头牛、2只羊共值金10两.2头牛、5只羊共值金8两.每头牛、每只羊各值金多少两？设1头牛值金 $x$ 两，1只羊值金 $y$ 两，则可列方程组为.

查看试题解析
13. 如图，正方形ABCD的边长为1，其面积标记为S₁ ，以AB为斜边向外作等腰直角三角形，再以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S₂ ， …按照此规律继续下去，则S₇的值为．

查看试题解析
14. 若 $\sqrt{x + 2}$ +（y-1）²＝0，则（x+y）²⁰²¹等于.

查看试题解析
15. 若关于x，y的二元一次方程组 ${\begin{matrix} 2 x + y = 4 k \\ 3 x + 2 y = 7 k \end{matrix}$ 的解也是二元一次方程x+0.6y=36的解，则k的值为.

查看试题解析
16. 若一个直角三角形的三边长分别为x，12，13，则x=.

查看试题解析
17. 如图，△ABC是等腰直角三角形，AC=BC，∠ACB=90°，点D是AB中点，在△ABC外取一点E，使DE=AD，连接DE，AE，BE，CE.若CE= $\sqrt{6}$ - $\sqrt{2}$ ， ∠ABE=30°，则AE的长为 .

查看试题解析
18. 正方形A₁B₁C₁O，A₂B₂C₂C₁ ， A₃BC₃C₂ ， …按如图所示的方式放置.点A₁ ， A₂ ， A₃ ， …和点C₁ ， C₂ ， C₃ ， …分别在直线y＝kx+b（k＞0）和y轴上，已知点B₁（1，1），B₂（2，3），则点B₃的坐标是，点Bn的坐标是 .

查看试题解析

三、解答题

19. 计算.

(1)、 $\sqrt[3]{8} + {(\frac{1}{2})}^{- 2} - {(\sqrt{2020} - 1)}^{0}$ ；

(2)、 $(2 + \sqrt{3}) (2 - \sqrt{3}) + \sqrt{12} - 3 \sqrt{\frac{1}{3}}$

查看试题解析
20. 解方程：

(1)、解方程组： ${\begin{matrix} 4 x - 3 y = 11 \\ 2 x + y = 13 \end{matrix}$ ；

(2)、解方程组： ${\begin{matrix} 3 (x - 1) = y + 1 \\ 5 (y - 1) = 3 (x + 5) \end{matrix}$ .

查看试题解析
21. 已知 $△$ ABC的三个顶点坐标分别为A(﹣1，4)，B(﹣3，4)，C(﹣5，2).

(1)、请在坐标平面内画出 $△$ ABC；

(2)、请在y轴上找一点P，使线段AP与BP的和最小，并直接写出P点坐标（保留作图痕迹）.

查看试题解析
22. 为了解学生每天回家完成作业时间情况，某中学对学生每天回家完成作业时间进行抽样调查，并将调查结果绘制成如图两幅不完整的统计图，根据图示，请回答下列问题：

(1)、被抽样调查的学生有 ▲ 人，并补全条形统计图；

(2)、每天回家完成作业时间的中位数是（小时），众数是（小时）；

(3)、该校共有2000名学生，请估计该校每天回家完成作业时间超过2小时的学生有多少人？

查看试题解析
23. 如图，已知直线l₁经过点A（5，0），B（1，4），与直线l₂：y＝2x-4交于点C，且直线1₂交x轴于点D.

(1)、求直线l₁的函数表达式；

(2)、求直线l₁与直线l₂交点C的坐标；

(3)、求 $△$ ADC的面积.

查看试题解析
24. 已知，△ABC和△DCE都是等边三角形，点B，C，E三点不在一条直线上（如图1）.

(1)、求证：BD＝AE；

(2)、若∠ADC=30°，AD=4，CD=5，求BD的长；

(3)、若点B，C，E三点在一条直线上（如图2），且△ABC和△DCE的边长分别为3和5，求AD的长.

查看试题解析
25. 某校准备组织八年级280名学生和5名老师参加研学活动，已知用1辆小客车和2辆大客车每次可运送120人；用3辆小客车和1辆大客车每次可运送135人.

(1)、每辆小客车和每辆大客车各能坐多少人？

(2)、若学校计划租用小客车m辆，大客车n辆，一次送完，且恰好每辆车都坐满.
①请你设计出所有的租车方案；

②若小客车每辆需租金6000元，大客车每辆需租金7500元，总租金为W元，写出W与m的关系式，根据关系式选出最省钱的租车方案，并求出最少租金.

查看试题解析
26. 如图1，在△ABC中，AB=AC，∠BAC=90°，D为AC边上一动点，且不与点A、点C重合，连接BD并延长，在BD延长线上取一点E，使AE=AB，连接CE.

(1)、若∠AED＝20°，则∠DEC＝度；

(2)、若∠AED＝α，试探索∠AED与∠AEC有怎样的数量关系？并证明你的猜想；

(3)、如图2，延长EC到点H，连接BH²+CH²＝2AE² ，连接AH与BE交于F，试探究BE与FH的关系.

查看试题解析
27. 如图，已知直线y=x-2分别与x轴，y轴交于A，B两点，直线OG：y=kx（k＜0）交AB于点D.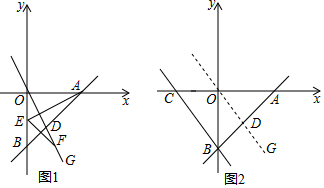

(1)、求A，B两点的坐标；

(2)、如图1，点E是线段OB的中点，连接AE，点F是射线OG上一点，当OG⊥AE，且OF=AE时，
①求EF的长；

②在x轴上找一点P，使PE+PD的值最小，求出P点坐标.

(3)、如图2，若k＝- $\frac{4}{3}$ ，过B点BC∥OG，交x轴于点C，此时在坐标平面内是否存在点M，使△BCM是以BC为腰的等腰直角三角形，若存在，直接写出点M的坐标；若不存在，请说明理由

查看试题解析